Homework & Assignments

HW# 7 | 6 | 5 | 4 | 3 | 2 | 1

Note / Answers

4.2

See the solutions to problem 4.3 for some useful path integral examples.

4.23
When it comes to finding $U(\myv r)$, you can guess a function, and then take its negative gradient to see if you're right.

Remember that $U(x,y,z)$ is a scalar function of position. (The gradient creates a vector function out of a scalar function.)

In these Calc III notes on the fundamental theorem is a Recipe to find the potential, given a conservative force, $\myv F(\myv r)$. We're using the physically meaningful relation that $\myv F=-\myv \nabla U(\myv r)$, whereas the Calc III convention is $\myv F=\myv \nabla f(\myv r)$.

All 3 forces depend only on position, $\myv r$. This is one criteria for a conservative force. A further test is that the curl of the vector field should vanish.

a.) $\myv \grad \times k(x\,\uv x+2y\,\uv y+3z\,\uv z)=(0,0,0)$, so $\myv F$ is conservative. The corresponding potential is $U=-k(\frac 12 x^2+y^2+\frac32 z^2)$.

b.) $\myv \grad \times k(y\,\uv x+x\,\uv y)=(0,0,1-1)=(0,0,0)$, so $\myv F$ is conservative. The corresponding potential is $U=-k(xy)$.

c.) $\myv \grad \times k(-y\,\uv x-x\,\uv y)=(0,0,1+1)=(0,0,2)$, so $\myv F$ is *not* conservative.

4.29

1. Involves sketching $U(x)$.

   It looks like a "flattened" parabola. After being kicked at $t$=0, the mass moves out to a maximum at $x=a$. It turns around and returns past the origin to $x=-A$ (because the well is symmetrical) and turns around again.

2. Argue that the total energy of the system is $E=kx_{\text{max}}^4=kA^4$, and then write out the integral (but don't solve it).

   At $x=A$, all the energy of the mass is potential (since that's where it stops before turning around). So the total energy of the system is $E=kA^4$.
   
   Using equation Taylor's equation [4.58], we can write the time to go from 0 to $x=A$ is $$t=\sqrt{\frac{m}{2}} \int_{x=0}^A\frac{dx'}{\sqrt{E-U(x')}}$$ The period is 4 times this number: $$\tau = 4t=\sqrt{8m} \int_{x=0}^A\frac{dx'}{\sqrt{kA^4-kx^4}}$$

3. The variable substitution is $u=x/A$. Write the new integral (including limits) in terms of $u$ (but don't solve it). But what you have should be enough to argue that the period is proportional to $1/A$ times some definite integral which no longer depends on $A$.

   If $u=x/A$, the when $x=0 \Rightarrow u=0$ and when $x=A \Rightarrow u=1$. Also $du=dx/A$. Making these substitutions into the integral: $$\begineq\tau =&\sqrt{8m} \int_{u=0}^1\frac{A\,du}{\sqrt{kA^4-ku^4A^4}}\\ =&\sqrt{8m} \int_{u=0}^1\frac{A\,du}{A^2\sqrt k \sqrt{1-u^4}}\\ =&\frac 1A \sqrt{\frac{8m}{k}} \int_{u=0}^1\frac{du}{\sqrt{1-u^4}} \endeq $$ Demonstrating the $1/A$ dependence

4. In this part, use CoCalc to solve that non-trivial definite integral with $k=m=1$ and also $A=1$. CoCalc will return a result in terms of a beta( ) function of two variables. (Here's some documentation on the beta function, which is in turn, defined in terms of the "gamma"($\Gamma$) function.) But practically, you can use N( ) to numerically evaluate the beta function for particular constant values.

   Mathematica will give the result in terms of a special function, EllipticK[some number]. Use N[EllipticK[...]] to evaluate the special function for that number.

With $m=k=A=1$, the integral for the period becomes: $$\begineq \tau=&\frac 11 \sqrt{\frac{8}{1}} \int_{u=0}^1 \frac{du}{\sqrt{1-u^4}}\\ =&\sqrt{8} *\text{"ElipticK[-1]"}=\sqrt 8* 1.31=3.71\endeq $$

4.41

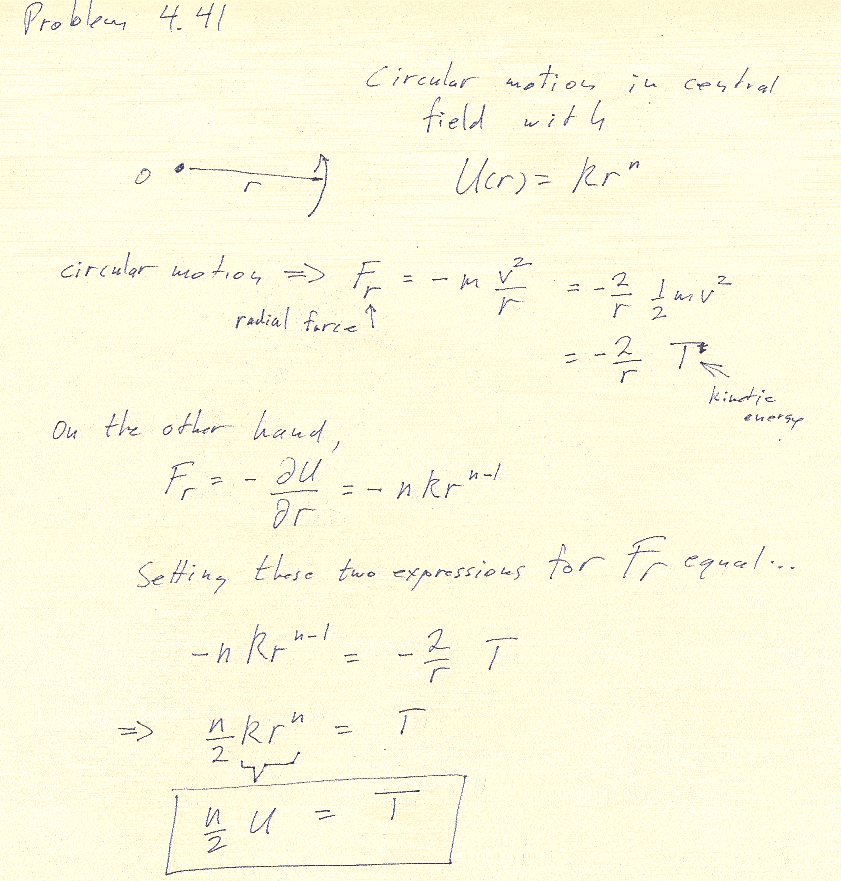
5.6
A spring oscillating with angular frequency $\omega$. Position at $t=0$ is $x_0 \gt 0$ and it's moving back towards the origin. Its amplitude is $2x_0$. Find the equation of motion in the form: $$x(t)=A\cos(\omega t -\delta).$$

The parameter $A$ is the amplitude, so $A=2x_0$. At $t=0$, $$x(0)=x_0=2x_0\cos(-\delta)$$ So, $\cos(-\delta)=1/2$. There are two solution, $\delta=\pm \pi/3$.

The initial speed should be towards the origin (that is, negative, since the initial position is positive): $$v_0=\frac{d}{dt}2x_0\cos(\omega t-\delta)|^{t=0}=-2x_0\omega\sin(-\delta)$$ This will be negative if the argument of the $\sin$ function is positive, so $\delta =-\pi/3$ and the motion of the mass on the spring is given by: $$x(t)=2x_0\cos(\omega t +\pi/3).$$

5.9

Since $\omega=\frac{2\pi}{\tau}$, the period is... $$\tau=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{k/m}}=2\pi\sqrt{m/k}.$$ Now, the total energy is $E=\frac 12mv^2+\frac 12 kx^2$.

At the origin, the energy is all in the form of kinetic energy: $E=\frac 12 mv_\text{max}^2$. At the maximum displacement, the speed is zero, so $E=\frac 12 kx_\text{max}^2$. Setting these two expressions for $E$ equal, we find: $$\frac 12 mv_\text{max}^2=\frac 12 kx_\text{max}^2.$$ With a little algebra, we find $\sqrt{m/k}=x_\text{max}/v_\text{max}=0.2\text{ m}/1.2\text{ m/s} = \frac 16\text{ s}.$ So, the period is $$\tau=2\pi\frac 1 6=\pi/3\text{ s}\approx 1.05\text{ s}.$$

5.13
Find the equilibrium position by finding the position, $r_0$, of the minimum of $U(r)$. Find $k$ by finding the second derivative of the potential function at equilibrium: $\frac{d^2}{dr^2}U(r)|^{r=r_0}=k$.

[CoCalc or Desmos]
The problem asks you to show that the PE has the form $U=\text{const}+\frac12kx^2$ close to the equilibrium position $r_0$ (where $r=r_0+x$). Instead, of doing this with algebra, show it graphically: Pick values for $U_0$, $R$, and $\lambda$. Calculate $r_0$ and $U(r_0)$ and $k$ for those values. Then graph the functions $U(r)$ and $U(r_0)+\frac12k(r-r_0)^2$ together on the same graph. Close to the equilibrium position the graphs should coincide closely.

Solution using Mathematica: 5.13.nb.pdf. Equilibrium point occurs at the minimum of potential energy: $$\begineq 0 =&\frac{\del U}{\del r}=\frac{d}{dr}U_0\left(\frac r{R}+\lambda^2\frac{R}{r}\right)\\ =& U_0\left(\frac 1{R}-\lambda^2\frac{R}{r^2}\right)\\ \endeq$$ Solving this for $r$, we find $r_0=\lambda R$.

To get the spring constant, evaluate the 2nd derivative of $U$ at the equilibrium position: $$\begineq \frac{d^2 U}{dr^2}=&\frac{d}{dr}U'=\frac{d}{dr}U_0\left(\frac 1{R} -\lambda^2\frac{R}{r^2}\right)\\ =& U_0\left(0+2\lambda^2\frac R{r^3}\right) \endeq$$ Substituting in $r\to r_0=\lambda R$ we get $$k=U_0 2\lambda^2\frac R{(\lambda R)^3}=\frac{2U_0}{\lambda R^2}$$

So, pick values for $\lambda$, $U_0$, and $R$. Then graph $U(r)$ and our approximation $U(r)\approx U(r_0)+\frac 12k(r-r_0^2)=2U_0\lambda+\frac 12 \left(\frac{2U_0}{\lambda R^2}\right)(r-r_0)^2$, and verify that at the bottom of the potential well, the two graphs look like they have the same curvature.

5.21

Don't forget to use the product rule when taking the derivatives of $x(t)=te^{-\beta t}$!

Calculating the first derivative: $$\dot x = \frac{d}{dt}te^{-\beta t}=e^{-\beta t}-\beta t e^{-\beta t}.$$ The second derivative: $$\begineq \ddot x = \frac{d^2}{dt^2}te^{-\beta t}=&-\beta e^{-\beta t}-\beta \left[e^{-\beta t}-\beta t e^{-\beta t}\right]\\ =&-2\beta e^{-\beta t}+\beta^2 t e^{-\beta t} . \endeq$$ Then, we plug these derivatives into the differential equation for the damped harmonic oscillator: $$\ddot x+2\beta \dot x+\omega_0^2x=0,$$ to show that it solves the equation as long as $\beta = \omega_0$, which is the condition for critical damping.

5.28

Start out by figuring out: Where is the final equilibrium position? Draw a free body diagram of the forces acting on the mass at this eventual equilibrium position: In terms of the spring constant, $k$, and the mass, $m$, you should be able to figure out how far the spring has to stretch to just balance the weight of the mass. From this, you can find $\omega$, even though you do not know $k$ or $m$.

At $t=0$, the mass is this far (the stretch at equilibrium) above its eventual equilibrium position.

The system is critically damped, so $\beta = \omega_0$ and $h(t)=C_1e^{-\beta t}+C_2te^{-\beta t}$.

To figure $\omega_0$, use the information that the spring stretches by $\Delta h=$-0.5 m when the mass, $m$, is attached. This means: $$\begineq F=&-k\Delta h\\ -mg=-k(0.5 m)\endeq$$ Therefore, $\omega_0=\sqrt{k/m}=\sqrt{g/(0.5m)}=\sqrt{(9.8m/s^2)/(0.5m)}=4.43\ s^{-1}$.

Now, use the initial conditions to find the constants. Relative to its equilibrium (stretched and not moving) position,
$$h(0)=0.5\ m=C_1$$ and $$\dot h(0)=0=-\beta C_1+C_2=-\omega_0(0.5)+C_2$$ So, $C_2=$(0.5 m)(4.43/s)=2.215 m/s, and substituting these into $h(t)$,

$h(1)=(0.5+2.215)e^{-4.43}=0.032\ m$.

At 1 second, the mass is 3.2 cm above its equilibrium position.

5.31

Each of the general solutions has two free constants. You need two constraints to fix the two constants. These constraints are your initial conditions: All of your solutions should start at x(0)=1, and are also released from rest which means $\dot{x}(0)=v(0)=0$.

With $\omega_0=2\pi$,

Underdamped: using $x(t)=e^{-\beta t}\cos(\omega_1t -\delta)$, and requiring $\dot{x}(t)=0$ leads us to $\delta=\arctan(\beta/\omega_1)$ and requiring $x(t)=1 \Rightarrow A=1/\cos\delta$, where $\omega_1=\sqrt{\omega_0^2-\beta^2}$

Critical damping: $x(t)=e^{-\omega_0 t}-\omega_0te^{-\omega_0 t}$ matches the initial conditions.

Overdamped: $x(t)=...$ (Luke)