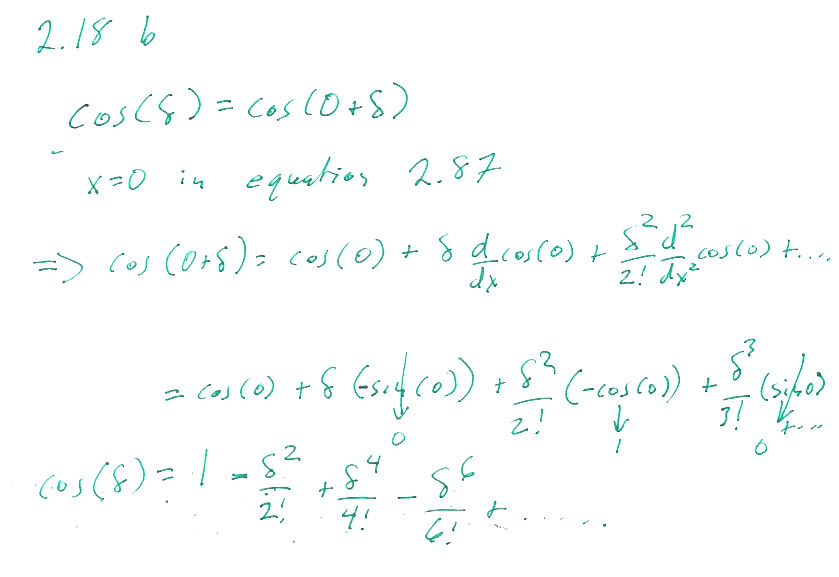Homework & Assignments
Homework #2
chapter 1 - PMR 1,
PMR 2, 36, 46, 50, 51. (See notes on 1.6,7.)
chapter 2- 4 (See notes on 2.1),
6, 10, 18ab
Notes
PMR 1
Solving it with Desmos by graphing x, sin(x), and
x-sin(x) < 0.1*x
$\sin(\theta)$ is within 10% of $x$ up until $\theta=0.786=45{}^o$
So, when $\theta\approx 0.79$, $\sin\theta \approx 0.9\, \theta$. (0.79 radians is about 45${}^o$.)
PMR 2
The general solution is $\phi(t)=A\sin(\sqrt{\frac gR t})+B\cos(\sqrt{\frac gR t})$.
The velocity is:
$$\dot\phi(t)=A\sqrt{\frac gr}\cos(\sqrt{\frac gR t})+B\sqrt{\frac gr}\sin(\sqrt{\frac gR t}).$$
We want the initial velocity at $t=0$ to be zero. Already, the sine function above goes to zero when $t=0$. But the cosine function does not vanish. So the only way to make sure that the initial speed is 0, that is $\dot\phi(0)=0$ is if $A=0$.
That leaves us with with
$$\phi(t)=B\cos(\sqrt{\frac gR t}).$$
We want $\phi(0)= \phi_0$. At $t=0$, the cosine function is 1, so we should set $B=\phi_0$, and the final solution, taking into account the initial conditions, is
$\phi(t)=\phi_0\cos(\sqrt{g/R}\,t)$.
1.36
b) Come up with a general equation for the horizontal distance at which release has to happen, and then plug in the particular value of height and speed given.
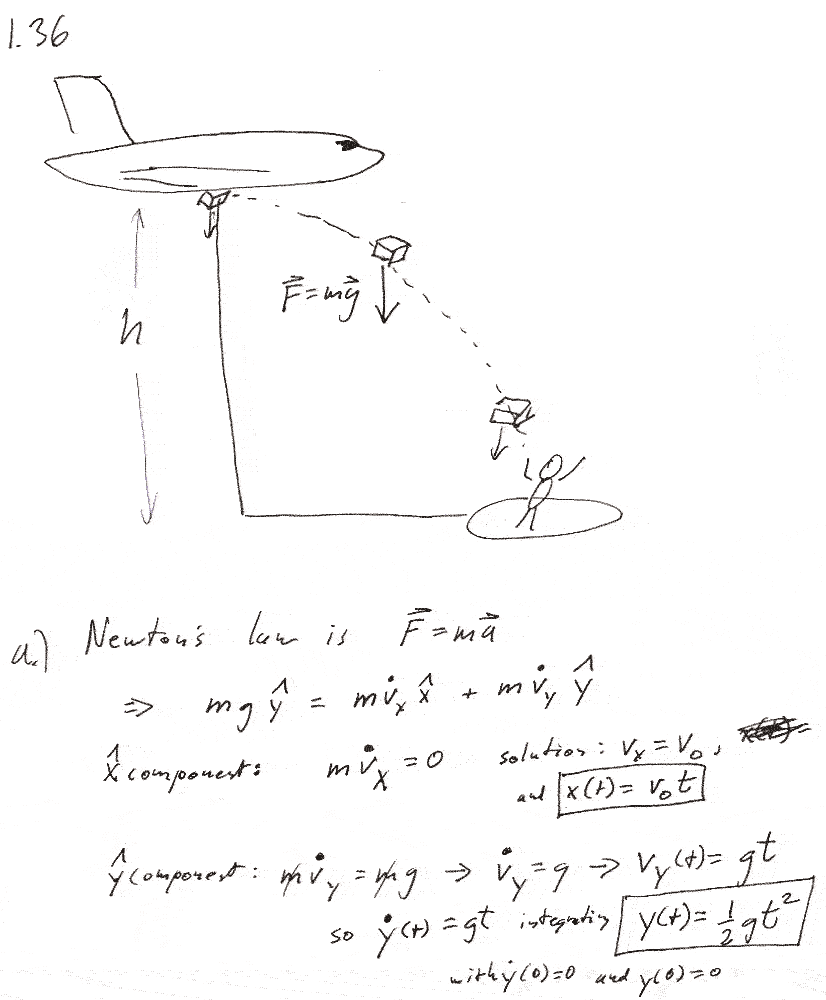

1.46

1.50
There will be a skate_diffeq notebook in CoCalc (look under handouts) to get you acquainted with solving differential equations in Jupyter / Sagemath.
1.51 Same as 1.50, but with $\phi_0=\pi/2$.
Hey, both 50 and 51 are 3-star problems! But once you have a Jupyter notebook with which to solve 50, you most likely will be able to just copy, paste, and tweak some of your code to have the skateboarder start at a different angle. And this starting angle will take you well outside the region where $\sin \theta\approx \theta$!
Here is a snapshot of an earlier version of that notebook.
Sagemath: Solving equations numerically
There are few SageMath commands to solve 2nd order diff eqs numerically, and none for higher-order diff eqs. But a large class of higher order equations can be converted to systems of coupled first order diff equations.
To use this approach you need to figure out how to convert a 2nd-order differential equation to a set of coupled, 1st-order differential equation. For example, like this!:

2.4
a.) An object moves a distance $\Delta x$ in a time $\Delta t$ (such that $v=\Delta x / \Delta t$). It has a cross sectional area, $A$, perpendicular to its motion.

So, it sweeps through a "tube" of air of volume $V=\Delta x\cdot A $ in time $\Delta t$. The mass of the air in the tube is $\Delta m=\rho V$.
[Now, what is the "rate at which the car encounters mass"?]
Therefore the "rate at which it encounters mass" is $$\frac{\Delta m}{\Delta t}=\frac{\rho \Delta x A}{\Delta t}=\rho A v.$$
b.) If the mass $\Delta m$ encountered in time $\Delta t$ were accelerated up to speed $v$, it would have kinetic energy $\frac 12 \Delta m v^2$, and the work done to accelerate it would be $F \Delta x$, where $F$ is the force we need to find.
Setting the work and kinetic energy equal, $F\Delta x = \frac 12\Delta m v^2$, and solving for $F$ we have:
$$ F=\frac 1{2\Delta x}\Delta m v^2=\frac 1{2\Delta x} (\rho A v \Delta t) v^2
=\frac 12\rho A v^2$$
since $\Delta t/\Delta x = 1/v$. The desired result was $F=\kappa \rho A v^2$ where $\kappa \lt 1$, which we certainly got.
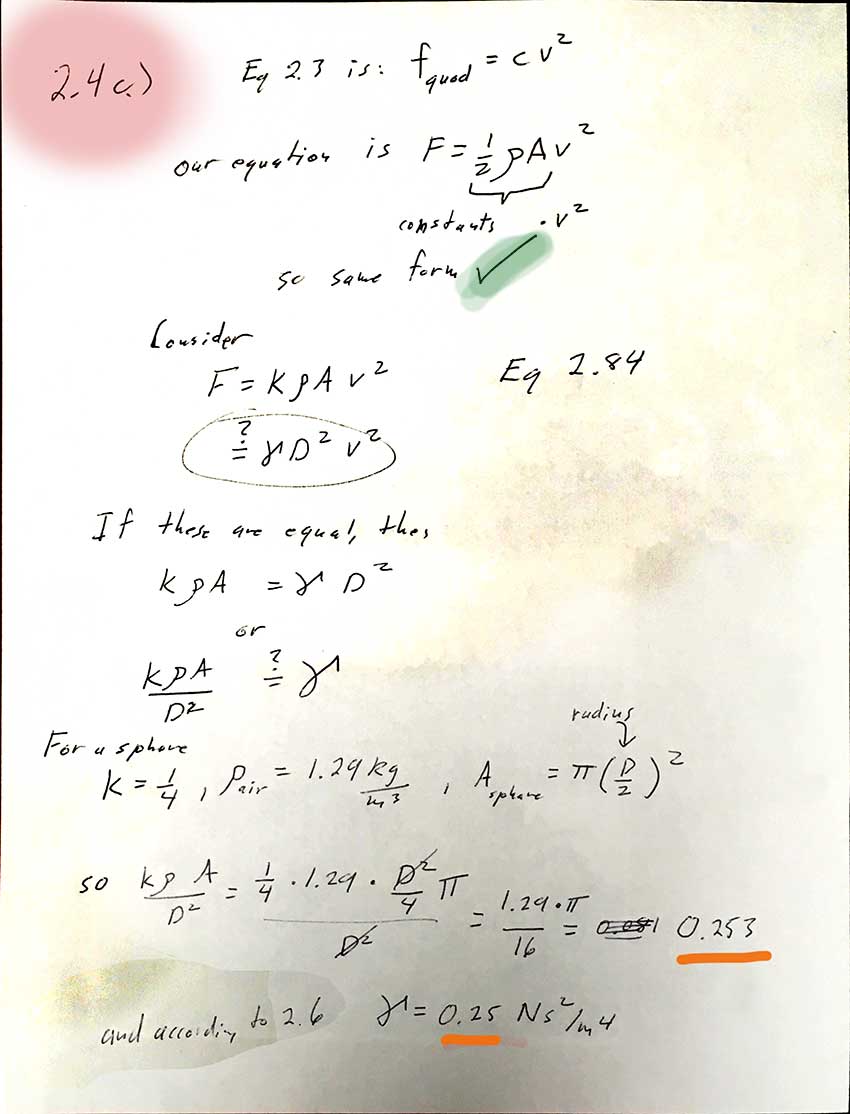
The power is proportional to what power of the speed? I didn't ask you this but...
Power is Energy / time, so we could write this as $\frac{F\Delta x}{\Delta t}=Fv$. Since $F\propto v^2$, apparently Power $\propto v^3$.
2.6
This problem involves a series expansion of the exponential. Be careful not to find yourself doing this: in a) "Let's only keep terms up to order $t$" and then in part b) "Oh here we need to keep terms up to $t^2$..."?
You shouldn't have to decide at an early stage how many terms to keep. Just keep them all (write out a couple of terms followed by "+..."). Put this whole series expansion in for $e^{-t/\tau}$ in the equation. *Then* look for cancellations, and *afterwards* make an argument about keeping only the lowest-power-in-$t$ terms that survive.

2.10
Were I to do this again, I would have given you the hint that:
You should find that $v_\text{ter}$ is less than without the buoyant force, but examine Taylor's equation 2.29 (and the discussion right afterwards): The terminal velocity will be different with the buoyant force, which will change the constant term in 2.29. But the relaxation time $\tau$ in the solution to 2.29 does not depend on the constant term. It only depends on the ratio $m/b$. So $\tau=m/b$ is unchanged by taking the buoyant force into account.
Perhaps also: When you write the magnitude of the buoyant force, the volume, $V$ of the ball bearing comes into play. Write the volume in terms of the mass of the sphere and the density of the steel.
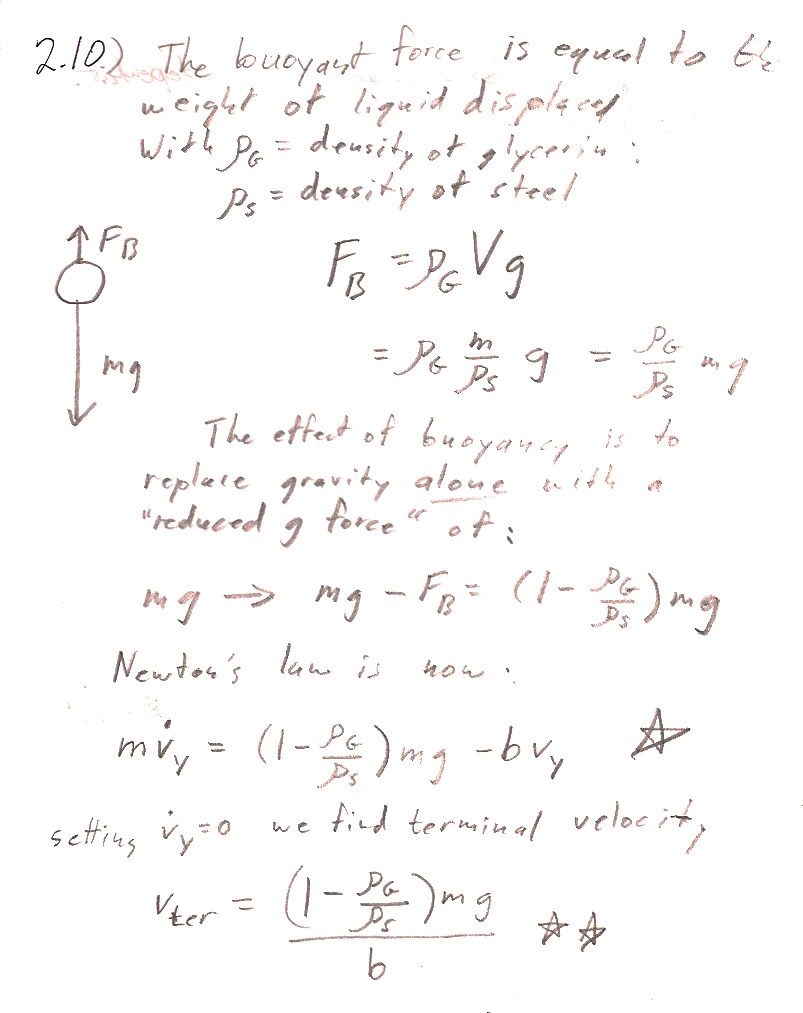
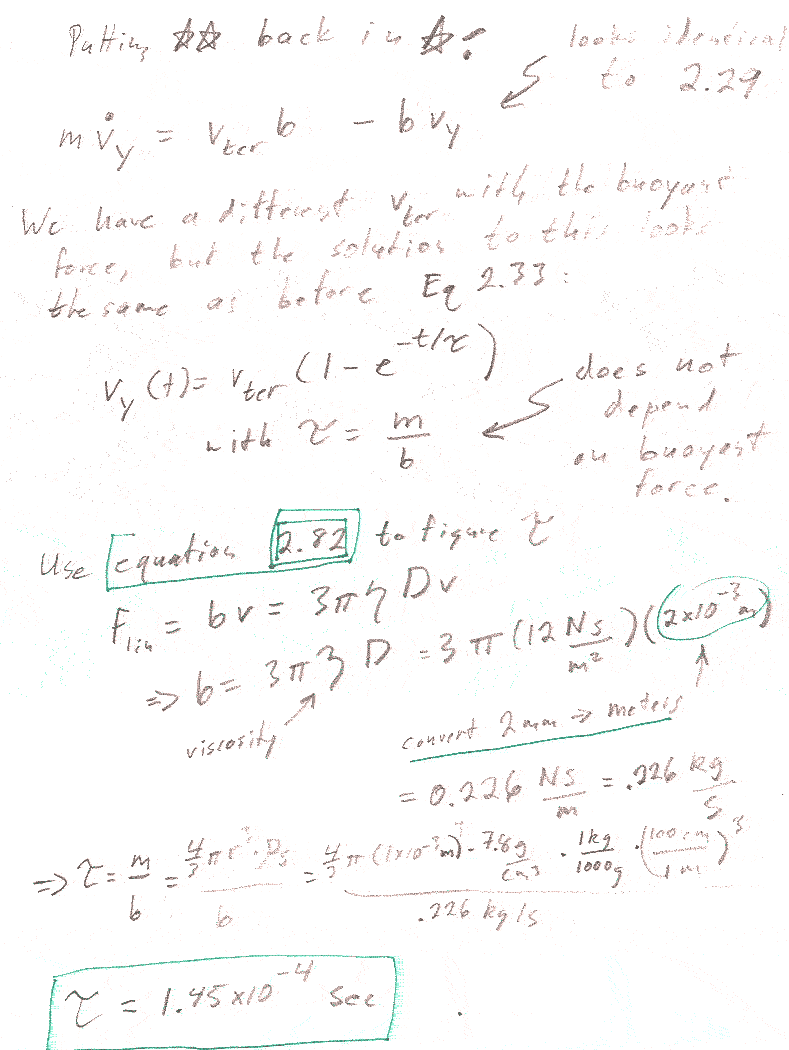
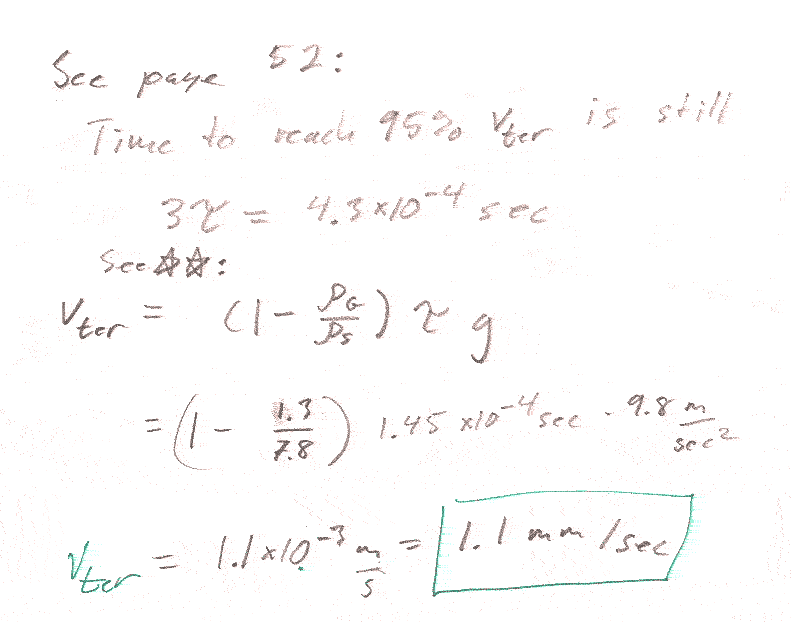
2.12


2.18 parts a and b only
Taylor expansions! - I have some notes on Taylor expansions here which may be useful if you haven't seen them before. We'll use them in several places throughout the course, so become friends with them! [I'll put a Taylor expansion on Exam 1.]
If you find our-textbook-Taylor's equation 2.87 slightly confusing, I prefer to think of it this way: The Taylor expansion of a function $f(x+\delta)$ near (or "around") $x=a$ can be thought of formally as function of $\delta$. Think of equation 2.87 as: $$\begineq \left.f(x+\delta)\right|^{x=a} =& \frac{1}{0!}\left.f(x)\right|^{x=a}\delta^0 +\frac{1}{1!}\left.\frac{df(x)}{dx}\right|^{x=a}\delta^1\\ & +\frac{1}{2!}\left.\frac{d^2f(x)}{dx^2}\right|^{x=a}\delta^2 +\frac{1}{3!}\left.\frac{d^3f(x)}{dx^3}\right|^{x=a}\delta^3+... \endeq$$ [I've stuck in $0!=1!=1$ and $\delta^0=1$ to show the progression in the pattern.] With this notation:
a.) $\ln (1+\delta)$ means you're expanding $\ln(x+\delta)$ about the value $x=a=1$ and
b.) $\cos(\delta)$ means you're expanding $\cos(x+\delta)$ about the value $x=a=0$.
a.)

Answer is
$$\ln(1+\delta)=\delta-\frac{\delta^2}{2}+\frac{\delta^3}{3}-\frac{\delta^4}{4}+...$$
Test it for $\delta =0.23$. Taking just the first 3 terms of the series expansion:
$$\begineq\ln(1+0.23)\approx (0.23)-\frac 12(0.23)^2+\frac 13{0.23}^3=&0.2076\\
\ln(1.23)=&0.2070 \ \text{[calculator]}\endeq$$
b.)