Homework & Assignments
Notes / Answers
Review the Chain rule.
3.25
This problem is easier if angular momentum is conserved. Is it?
Newton's equation for angular momentum (instead of linear momentum) is: $$\dot{\myv{\ell}} = \myv{\Gamma}$$ Where $\myv{\Gamma}=\myv F \times \myv r$ is the torque. Start by making an argument that angular momentum *is* conserved.
The only non-normal force $\myv F$ is always directed along the part of the string connected to the mass, and the vector $\myv r$ between the origin about which the angular momentum is calculated, and the point of application of the force is also directed along the same portion of the string. The cross product of two parallel vectors is 0, so $\myv{\Gamma}$ is 0, so the magnitude of the angular momentum, $\ell$, is not changing.
Conservation of angular momentum means $$\ell=I\omega=mr^2\omega=mr_0^2\omega_0$$ Therefore, if you change $r$, the new angular speed will be $$\omega=\omega_0\frac{r_0^2}{r^2}.$$
3.32 The moment of inertia is $$I=\sum m_i{\frak r}^2_i\to\int dm\cdot {\frak r}^2$$ where ${\frak r}$ is the distance of the chunk of mass $dm$ from the axis of rotation (the $z$ axis). How can you express this in terms of spherical polar coordinates?
- A little chunk of mass $dm$ occupies a volume $dV$. Using $D=$mass density, we can write $dm=D\,dV$
- In spherical polar coordinates, $dV=r^2\sin\theta\,dr\,d\theta\,d\phi$.
- In spherical polar coordinates, the distance to the $z$-axis is ${\frak r}=r\sin\theta$.
Putting this together, $$\begineq I=&\iiint (r\sin\theta)^2D\,dV\\ =&\iiint r^2\sin^2\theta\,D\,r^2\sin\theta\,dr\,d\theta\,d\phi\\ =&D\color{blue}\int_{r=0}^R r^4\,dr \color{red}\int_{\theta=0}^\pi \sin^3\theta\,d\theta \color{black}\int_{\phi=0}^{2\pi}d\phi\\ =&\frac{M}{\frac 43 \pi R^3}\color{blue}\frac{R^5}{5} \color{red}\frac 43 \color{black}2\pi\\ =&\frac 25 M R^2. \endeq $$
4.3
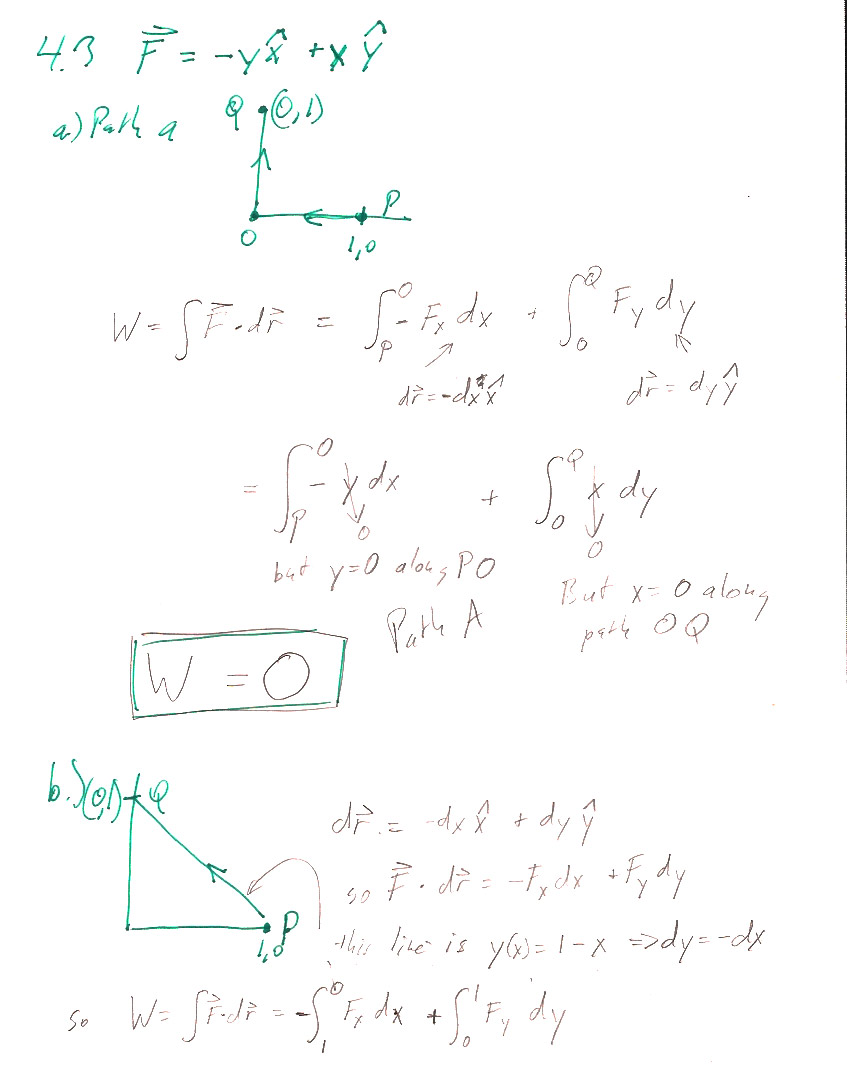
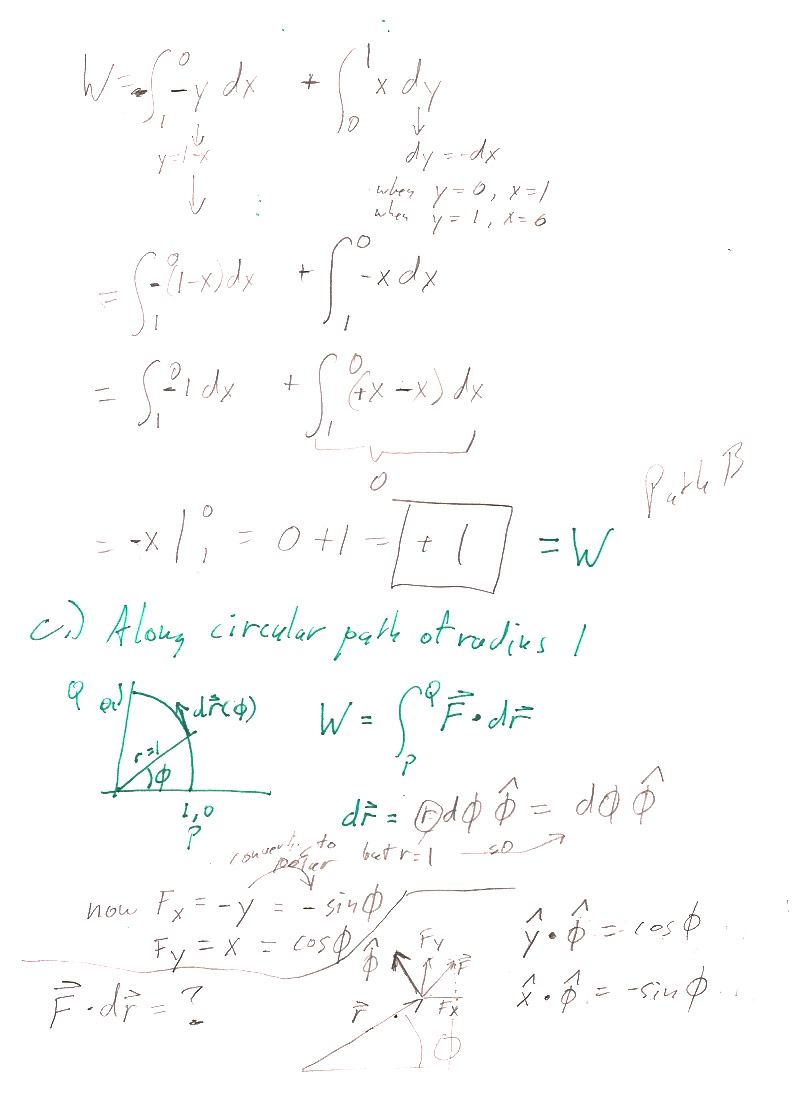
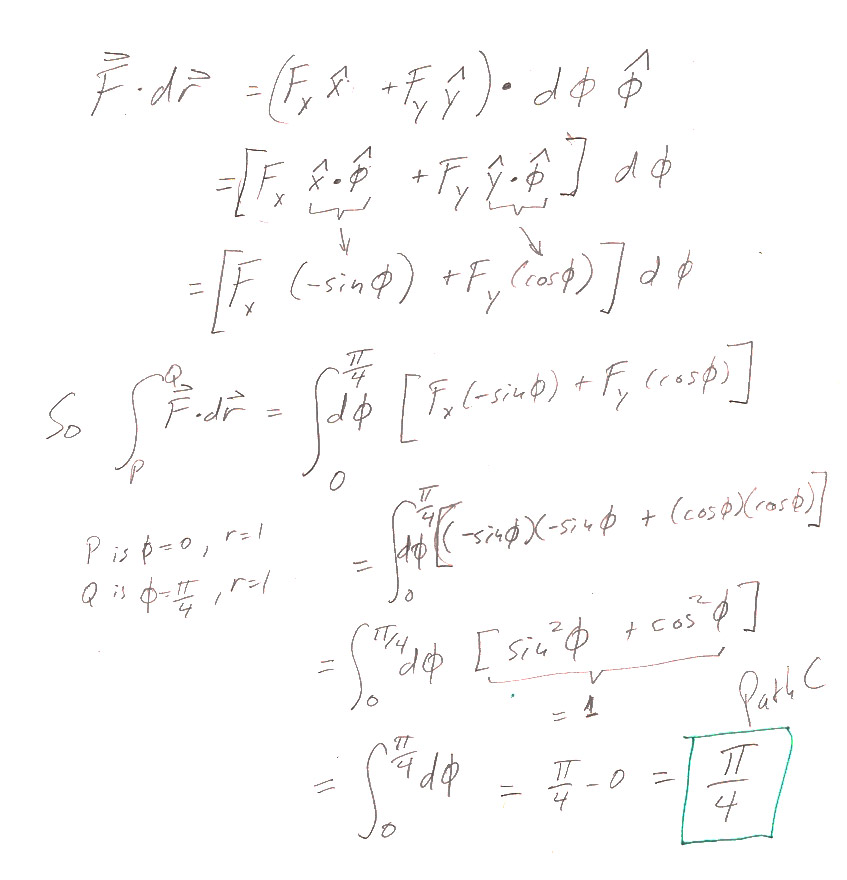
4.4
a.) Just like in 3.25, momentum is conserved.
$$\omega=\omega_0\frac{r_0^2}{r^2}.$$
b.) Figure out the force (tension in the string) needed to keep a mass $m$ moving with speed $\omega$ in a circle of radius $r$, and then integrate to find the work done
The force (tension in the string) needed to keep a mass $m$ moving with angular speed $\omega$ in a circle of radius $r$, is the mass times the centripetal acceleration : $$F_c=m\omega^2 r$$ So, the total work needed to change the radius from $r_0$ to $r$ is: (The negative sign is there to make the result come out positive, despite going from a large radius, $r_0$, to a smaller radius $r$.) $$\begineq -\int_{r_0}^r F_c\,dr&=&-\int_{r_0}^r m\omega^2r\,dr= -\int_{r_0}^r m\left(\omega_0\frac{r_0^2}{r^2}\right)^2r\,dr \\ &=& -m\omega_0^2r_0^4\int_{r_0}^r \frac1{r^3}\,dr\\ &=& m\omega_0^2r_0^4 \frac12\left(\frac1{r^2}-\frac1{r_0^2}\right) \endeq $$
c.) The change in kinetic energy is $$\Delta T=\frac12mv^2-\frac12mv_0^2 = \frac12mr^2\omega^2-\frac12mr_0^2\omega_0^2$$ which works out to the same result as b) after substituting in for $\omega^2=\left(\omega_0\frac{r_0^2}{r^2}\right)^2$.
4.5
a.) - When it's time to take $\myv F_g \cdot d\myv r$, you can resolve
$d\myv r$ into its components, as $d\myv r = dx\,\uv x+dy\,\uv y+dz\,\uv z$.
If a force is conservative then $W(1\to 2)$ is path independent. Here, the force of gravity is $\myv{F}_g=-mg \uv{y}$, so the work to go between two points is... $$\begineq W(1\to 2)&=&\int_1^2 \myv F \cdot d\myv{r}= \int_1^2 (-mg)\uv y \cdot \left[dx\,\uv x+dy\,\uv y+dz\,\uv z\right]\\ &=&\int_1^2 (-mg)dy = -mg(y_2-y_1)=-mg\Delta h \endeq$$ No matter what path is taken between points 1 and 2, the height difference is the same, so this integral is not path dependent, and therefore the force is conservative.
b.)
For the gravitational force, $U(\myv r) = -W(0\to \myv r) + C = mgy + C$. If the potential is to be 0 at $y=0$, then $C=0$, and $U(\myv r)=mgy$.
4.8
- Using energy conservation $$\begineq -\Delta U=&\Delta T\\ mg\Delta h=&\frac 12mv^2 \endeq$$
- A puck moving on the surface of a sphere requires a normal force greater than or equal to the centripetal acceleration to keep moving in a circle, where $$F_c=m\frac{v^2}R=2\frac{mg\Delta h}{R}.$$
- The source of that normal force is gravity. The component of gravity normal to the bowling ball surface is $F_N=mg\cos \theta$ where $\theta$ is the angle from the top of the bowling ball.
- The height difference $\Delta h$ can be expressed in terms of $\theta$: $$\Delta h=R-R\cos \theta=R(1-\cos\theta).$$
4.12
a.) $\myv \grad f = 2x\,\uv x+3z^2\,\uv z$
b.) $\myv \grad f = k\,\uv y$
c.) You can take the gradient in Cartesian coordinates. If you do this, look at your final result (in terms of $x$, $y$, and $z$) and try to write as many parts of it as possible in terms of things like $r=\sqrt{x^2+y^2+z^2}$ and $\myv r=x\uv x+y\uv y+z\uv z$.
An alternate approach is to use the expression for the gradient in spherical polar coordinates.
c.) Most of you found that you could write the gradient of $\myv r$ as:
$$\myv \nabla r = \frac{x}{\sqrt{x^2+y^2+z^2}}\uv x +\frac{y}{\sqrt{x^2+y^2+z^2}}\uv y +\frac{z}{\sqrt{x^2+y^2+z^2}}\uv z
$$
but this can be simplified further...
$$=\frac{1}{\sqrt{x^2+y^2+z^2}}\left[x\uv x+y\uv y+z\uv z \right] = \frac{1}{r}[\myv r] = \frac{1}{r}[r \uv r] = \uv r$$
Alternate solution: Use the expression for the gradient in spherical polar coordinates, since $r$ is the polar coordinate $r$, the distance from the origin.
The function $f(r,\theta,\phi)=(r)$, and the gradient expression has only one non-zero term, since partial derivatives of $r$ wrt $\theta$ and $\phi$ are zero.
$$\myv \nabla (r)=\uv r \frac{\del}{\del r}(r)=1\,\uv r=\uv r.$$
d.)
Use the expression for the gradient in spherical polar coordinates. The function $f(r,\theta,\phi)=(1/r)$, and the gradient expression has only one non-zero term:
$$\myv \nabla (1/r)=\uv r \frac{\del}{\del r}(1/r)=-\frac 1{r^2}\,\uv r.$$
But, typically, you did this with cartesian coordinates, and you found:
$$\myv \nabla (1/r) = -\frac{x}{(\sqrt{x^2+y^2+z^2})^3}\uv x -\frac{y}{(\sqrt{x^2+y^2+z^2})^3}\uv y -\frac{z}{(\sqrt{x^2+y^2+z^2})^3}\uv z
$$
Which simplifies to $-\myv r/r^3=-\frac{1}{r^2}\uv r$.
4.15
Using $\myv\grad f\cdot d\myv r=0.44$.
Exact result $f(\myvr+\Delta r)-f(\myv r)=0.4494$.
4.30
Come up with an expression for the height of the center-of-mass, $H(\theta)$ as a function of the angle, $\theta$, that the toy is tipped away from vertical. Your function will additionally depend on the height, $h$, of the CM when vertical, as well as $R$. Then you can express the potential energy as a function of one degree of freedom, $U(\theta)$.
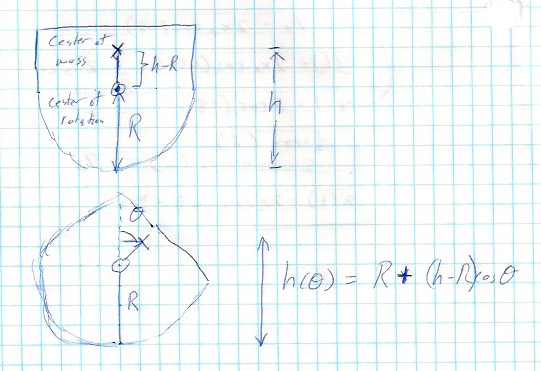
The height of the center of mass when the toy is tipped by an angle $\theta$ is
$H(\theta)=R+(h-R)\cos \theta$.
Therefore
$U(\theta)=mgH=mg\left[R+(h-R)\cos \theta
\right]$.
The "restoring force" is the gradient of the potential energy. Therefore, an equilibrium position is found where the gradient =0, that is: $$\frac{dU}{d\theta}=0=-mg(h-R)\sin\theta$$ This means there is an equilibrium at $\theta=0$.
To figure out the stability of any equilibrium point, you need to figure the curvature (second derivative) of the potential energy function, $U(\theta)$.
That is, we have stability when the curvature at the equilibrium position is positive:
$$\frac{d^2U}{d\theta^2}|^{\theta=0}=-mg(h-R)\cos\theta|^{\theta=0}=mg(R-h)$$
This is positive as long as $R\gt h \Rightarrow $ The center of mass is below the center of rotation of the toy.
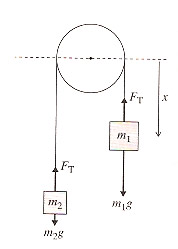4.31 - The Atwood machine.
If $x$ is the coordinate of the right weight, and $y$ is the coordinate of the left weight, Then the two are connected by a rope of a fixed length, so $x+y=k \Rightarrow y=k-x$. Take the time derivative of this: $\dot y=-\dot x$, that is, $v_y=-v_x$.
Adding up the potential and kinetic energies: $$\begineq E =& \frac{1}{2}m_2\dot y^2 -m_2gy +\frac{1}{2}m_1\dot x^2 - m_1gx\\ =& \frac{1}{2}m_2(-\dot x)^2 - m_2g(k-x) +\frac{1}{2}m_1\dot x^2 - m_1gx\\ =& \frac{1}{2}m_2\dot x^2 + m_2gx-m_2gk +\frac{1}{2}m_1\dot x^2 - m_1gx\\ =& \frac{1}{2}(m_2+m_1)\dot x^2 - m_2gk+(m_2-m_1)gx\endeq$$
When "an equation of motion" is asked for, the idea is to calculate the acceleration. ($F=ma$ is the prototypical equation of motion).
But instead of analyzing forces, you can also get the accelerations by
coming up with expressions for the potential and kinetic energy
of the system. As long as we can ignore friction, total mechanical energy is conserved:
$$0 = \frac{dE}{dt} = \frac{d(T+U)}{dt}$$
which often results in an expression that you can solve for an acceleration. If you think about it, kinetic energy almost always involves a speed (squared). So $dT/dt$ should contain some second derivate (acceleration).
$$\begineq 0 = \frac{dE}{dt} =&(m_2+m_1)\dot x \ddot x+(m_2-m_1)g\dot x\endeq$$ dividing out by the factors of $\dot x$, this can be written as: $$(m_1+m_2)\ddot x = (m_1-m_2)g,$$ or, re-arranging for the acceleration: $$\ddot x = \frac{m_1-m_2}{m_1+m_2}g.$$
Now consider instead thinking about this in terms of the tension in the rope, $F_T$. On the left, $\ddot x$ is the upwards acceleration, and writing $ma=\sum (forces)$ on the left, we get: $$m_2\ddot x = F_T-m_2g \Rightarrow F_T=m_2(\ddot x+g).$$ On the right, $\ddot x$ means a downward acceleration, so... $$m_1\ddot x = m_1 g-F_t \Rightarrow F_t= m_1(g-\ddot x)$$ Setting these two expressions for $F_T$ equal to each other... $$m_2(\ddot x+g)=m_1(g-\ddot x)$$ Solving for $\ddot x$, gives once again... $$\ddot x = \frac{m_1-m_2}{m_1+m_2}g.$$