Homework & Assignments
Homework #3
chapter 2 - 17, 20
, 23, 27, 40, 46, 47, 55 (a and b only)
chapter 3 - 4, 10, 12, 17
Notes &
2.20
Here's an example of parametric plotting in Desmos.
For the limit as $\tau\to \infty$, you *could* just put a really big number in for $\tau$ to get an approximate plot. Or, you could be more precise by writing the exponential as a Taylor series and then taking the limit as $\tau\to\infty$.
$e^{-t/\tau}=1-t/\tau+(t/\tau)^2/2-...$ So, $$\begineq\tau(1-e^{-t/\tau})=&\tau(1-(1-t/\tau+(t/\tau)^2/2-..))\\ =&\tau(t/\tau-(t/\tau)^2/2+..))\\ =&t-(t^2)/2\tau+..\\ \approx& t.\endeq$$ With the constants all set to 1, and in the limit as $\tau\to\infty$, you should find that... $x(t)\to t$ and $y(t)\to t-\frac 12t^2$.
2.23
Using Taylor's equation 2.59 for a sphere of diameter $D$, in a medium with characterized by a resistive coefficient $\gamma$, the terminal speed due to quadratic air resistance (in m/sec) is:
$$v_\text{ter}=\sqrt{\frac{mg}{\gamma D^2}}$$
where $\gamma=$0.25Ns${}^2$/m${}^4$ for air for all of these calculations.
a.) $D=$0.003 meters, $m=1.13\times 10^{-4}$ kg
$\Rightarrow$$v_\text{ter}=22.2$ m/s $\approx$ 50 mph
b.) $D=$0.12 meters, $m=7.26$ kg $\Rightarrow$$v_\text{ter}=140.6$ m/s $\approx$ 315 mph
c.) $D=$0.557 meters, $m=90.7$ kg $\Rightarrow$$v_\text{ter}=107.1$ m/s $\approx$ 240 mph. (According to www.fai.org about 120 mph laid out flat with belly down.).
2.27
For both 2.27 and 2.40 the general strategy is:
- Write down the equation of motion in the form: $$m\frac{dv}{dt}=[\text{sum of forces depending on powers of }v]$$
- use separation of variables, and integrate $$\int_{v_0}^v [\text{terms depending on }v]\,dv=\int_0^t dt.$$


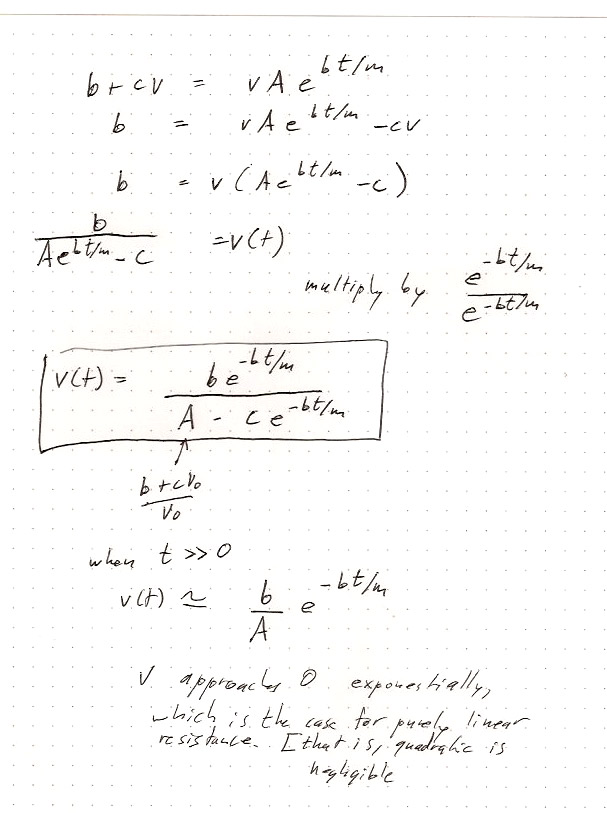
2.40
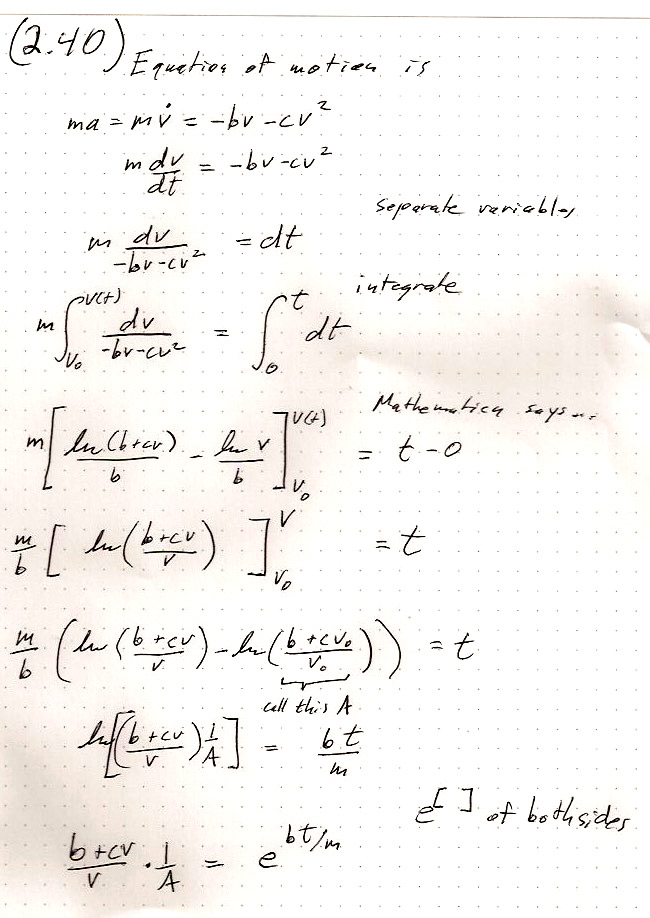
2.46


A sketch of $z=5e^{i\omega t}$ has a vector of length 5 rotating CCW. $z^*$ is the reflection of $z$ around the $x$ axis, and it rotates CW:
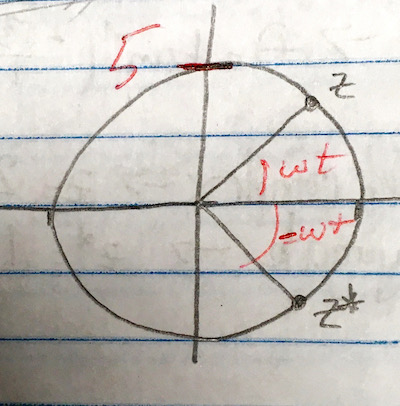
2.47
- $z+w=9+4i;\ \ \ z-w=3+12i;$
$z\times w=(6+8i)(3-4i)=18-24i+24i-32i^2=18+32=50$
$\frac zw=\frac{zw^*}{ww^*}=\frac{(6+8i)(3+4i)}{(3-4i)(3+4i)}= \frac{18+24i+24i+32i^2}{9-16i^2}=\frac{1}{25}(-14+48i)=2e^{-1.287i}$ - $z=4+i4\sqrt 3;\ \ \ w=2\sqrt 3+2i$
$z+w=7.46+8.93i;\ \ \ z-w=0.536+4.928i$
$zw=8*4e^{i(\pi/3+\pi/6)}=32e^{i\pi/2}=32i;\ \ \ z/w=(8/4)e^{i(\pi/3-\pi/6)}=2e^{i\pi/6}$
2.55ab
When you're setting up the
equation of motion using the Lorentz force, $\myv F=q(\myv v \times \myv B + \myv E)$, you will need to put in the general variable for velocity $\myv v$. Not $\myv v(t=0)=v_0 \uv x$, because, of course, that initial value is a constant and
can never change with time.
In part a.) You show that $\dot v_z=0$. Good, but that's not enough to show that the particle remains in the $xy$ plane. This just means $v_z(t)$ is constant, $v_z(0)$. I was looking for you to acknowledge that $\myv v_0=(0,v_{x0},0)$ so $v_z(0)=0$.
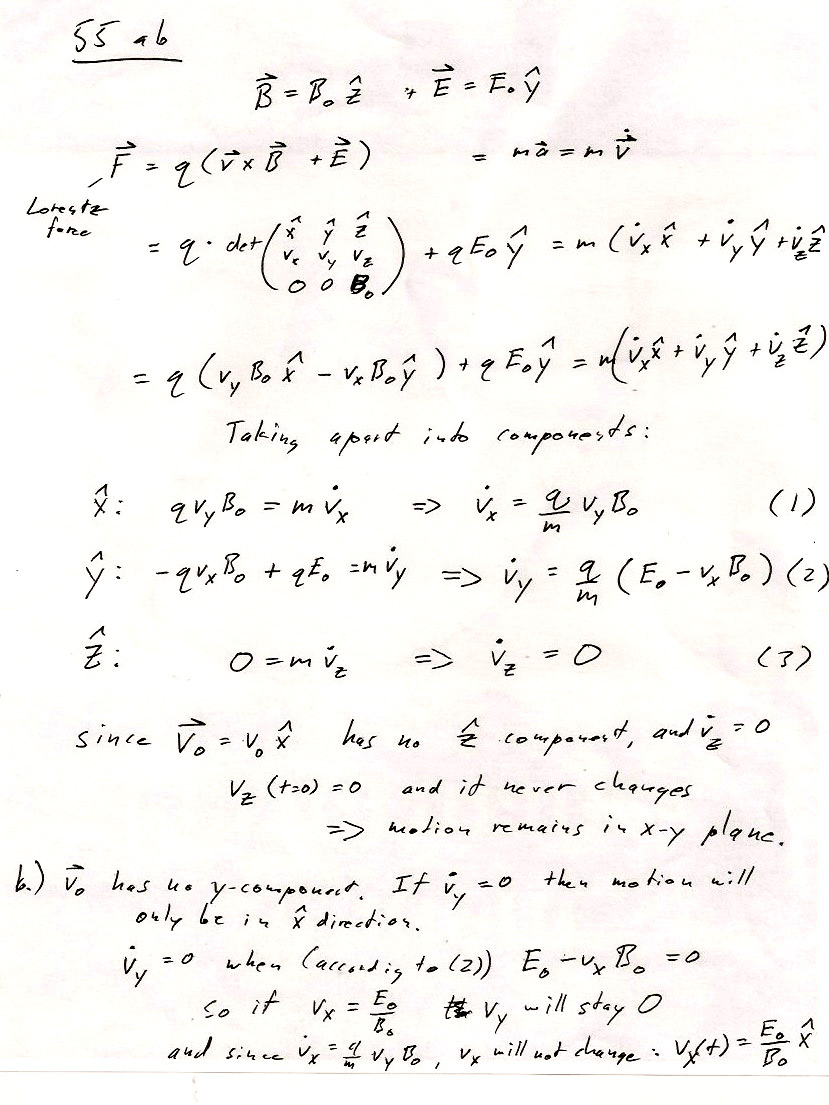
3.4
This is a 1-dimensional problem. In class, we talked about how you might label the speeds involved. Are you going to say that any speed is positive going to the right, and so left-going objects have a negative speed? Or will you use speed variables that are positive, but then think carefully about the pluses and minuses in your equations?
In any case, you know that momentum conservation will be one equation, and the condition about relative speeds gives you another equation, and two equations should be enough to determine two unknown speeds in terms of other
In part b) It may be useful to think of a coordinate system which is at rest with respect to the the moving car that results from the first part. Since the coordinate system is moving at a constant speed (no acceleration) the initial momentum of the car with 1 hobo can be zero in that reference frame.



3.10
You can use equation 3.8 (set the initial speed, $v_0=0$) for the speed $v(t)$. Multiply by $m$ to get the momentum. And don't forget when taking derivatives that the mass of the rocket, $m(t)$ is a function of time!
The momentum, $p(t)=m(t)v(t)$. So, starting from eq. 3.8: $$p=mv_{ex}\ln(m_0/m).$$ The maximum momentum of the rocket occurs when $\dot p=0$: $$\begineq \dot p &=& v_{ex}\left[\dot m \ln(m_0/m)+m\frac{d}{dt}(\ln m_0-\ln m)\right]\\ &=&v_{ex}\left[\dot m \ln(m_0/m)+m(-1/m)\dot m\right]\\ &=&\dot m v_{ex}\left[ \ln(m_0/m)-1\right]\\ \endeq$$ The maximum occurs when $[...]=0$, that is, when $$\ln(m_0/m)=1 \Rightarrow m=m_0/e$$ Several of you used some approximations and found $m=m_0/3$. This is really close, since $e=2.79 \approx 3$!
3.12
You can use equation 3.8 for the speed $v(t)$.
a.) $v_{\text{final}}=0.92 v_{ex}$. b.) $v_{\text{final}}=0.357 v_{ex}+0.693 v_{ex}=1.050 v_{ex}$.