The field of a magnetized body
As with electric polarization, we will start by considering magnetized bodies, without asking about the field that magnetized them.
- The vector potential in terms of bound volume current, and bound surface current.
- Examples
The magnetic vector potential of a single dipole $\myv m$ is: $$\myv A(\myv r) = \frac{\mu_0}{4\pi}\frac{\myv m \times \uv \rr}{\rr^2}.$$
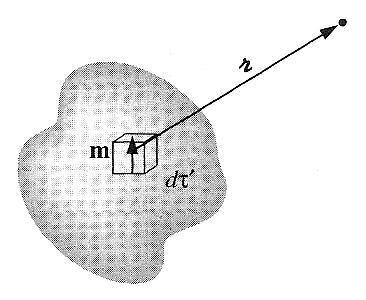 An object with a net magnetization per unit volume $\myv M(\myv r')$ then
has a dipole moment
$\myv m$ at $\myv r'$ of $\myv M d \tau'$. Summing to find the overall vector
potential:
$$\myv A(\myv r) = \frac{\mu_0}{4\pi}\int \frac {\myv M(\myv r') \times \uv{\rr}}{\rr^2}
d \tau '.$$
An object with a net magnetization per unit volume $\myv M(\myv r')$ then
has a dipole moment
$\myv m$ at $\myv r'$ of $\myv M d \tau'$. Summing to find the overall vector
potential:
$$\myv A(\myv r) = \frac{\mu_0}{4\pi}\int \frac {\myv M(\myv r') \times \uv{\rr}}{\rr^2}
d \tau '.$$
 By manipulating
$(\myv\grad)' \frac{1}{\rr}=\frac{\uv\rr}{\rr^2}$ along the lines of what we did
to arrive at expressions for bound volume
charge and bound surface charge, we can re-write the expression above in
terms of a volume integral and a surface integral...
$$\myv A(\myv r)=\frac{\mu_0}{4\pi}\int_{\cal V}\frac{\myv J_b(\myv r')}{\rr}d \tau'+\frac{\mu_0}{4\pi}\int_{\cal S}\frac{ \myv K_b(\myv r') }{\rr} da'.$$
By manipulating
$(\myv\grad)' \frac{1}{\rr}=\frac{\uv\rr}{\rr^2}$ along the lines of what we did
to arrive at expressions for bound volume
charge and bound surface charge, we can re-write the expression above in
terms of a volume integral and a surface integral...
$$\myv A(\myv r)=\frac{\mu_0}{4\pi}\int_{\cal V}\frac{\myv J_b(\myv r')}{\rr}d \tau'+\frac{\mu_0}{4\pi}\int_{\cal S}\frac{ \myv K_b(\myv r') }{\rr} da'.$$
The first term is the bound volume current: $$\myv J_b = \myv \grad \times \myv M,$$
and the second term has been written in terms of a bound surface current and the unit vector normal to the surface as $$\myv K_b = \myv M \times\uv{n}.$$
Problem 6.8
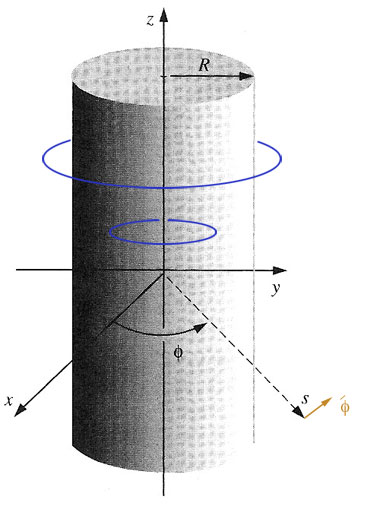 A long cylinder of radius $R$ carries a magnetization $\myv M= ks^2 \uv\phi$.
Find the magnetic field.
A long cylinder of radius $R$ carries a magnetization $\myv M= ks^2 \uv\phi$.
Find the magnetic field.
Strategy outline:
- Find the bound volume current density,
- Find the bound surface current density,
- Use these, together with Ampere's law to find $\myv B$ (Fugetabout the vector potential).
The bound volume current density is: $$\myv J_b = \myv \grad \times \myv M$$
Use the cylindrical form of the curl; $\myv M=M(s)\uv\phi$: $$\begineq \myv J_b &=\frac{1}{s}\frac{\del}{\del s}(s(ks^2))\uv{z}\\ &=\frac{1}{s}3ks^2 \uv{z}=3ks\uv{z}.\endeq$$
This is a (volume) current density flowing upwards. The total body bound current (going up in the $z$ direction) is... $$I_{b\text{ up}}=\int (\myv J_b)_z 2\pi s ds = \int_0^R 3ks 2\pi s ds = 2\pi k R^3.$$
Now to find the surface current density. First on the rounded surface: $$\myv K_b = \myv M \times\uv{n}=kR^2 \uv\phi \times\uv{s} = -kR^2\uv{z}.$$
The total surface current going down (in the $z$ direction) is... $$I_{s \text{ down}} = \oint \myv K_z R \,d \phi = \oint (-kR^2) Rd \phi= -kR^3 2\pi.$$
So the total body current going up just balances the total surface current going down.
[I haven't calculated the surface current on the flat top or bottom of the cylinder...]
We have a known current distribution and azimuthal symmetry--Auspicious for using Amperes' law:
$\myv B$ field should be circulating around the cylinder axis, (in the same direction as it does around a wire). That is $\myv B = B(s)\uv{\phi}$.
Using an Amperian loop outside the cylinder: The total current piercing this loop is zero, so $\myv B = 0$ outside the cylinder.
Inside the cylinder (smaller Amperian loop): $$\oint \myv B dl = \mu_0I_\text{enc},$$ $$\Rightarrow 2\pi s B = \mu_0\int_0^s \myv J_b \cdot d \myv a' = \mu_0\int_0^s 3ks' 2\pi s' ds'=\mu_0 2 \pi ks^3$$
$$B_{\phi\text{ inside}}=\mu_0ks^2=\mu_0 M.$$
Problem 6.10
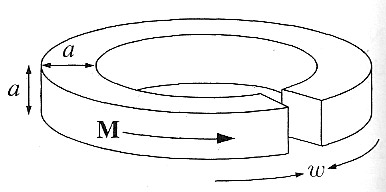 An iron rod of length $L$ and square cross section (side $a$) is given a uniform longitudinal magnetization $\myv M$, and then bent around in to a circle with a narrow gap (width $w$) as shown. Find the magnetic field at the center of the gap, assuming $w \ll a \ll L.$ [Hint: Treat it as the superposition of a complete torus plus a square loop with reversed current.]
An iron rod of length $L$ and square cross section (side $a$) is given a uniform longitudinal magnetization $\myv M$, and then bent around in to a circle with a narrow gap (width $w$) as shown. Find the magnetic field at the center of the gap, assuming $w \ll a \ll L.$ [Hint: Treat it as the superposition of a complete torus plus a square loop with reversed current.]
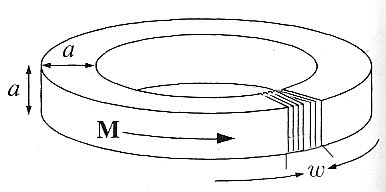 The idea is to replace the problem with a solid bar of uniform magnetization, and then an applied surface current $\myv K = -\myv K_b$. Let's first calculate the field in the solid torus, by way of finding all the (bound) current in the problem.
The idea is to replace the problem with a solid bar of uniform magnetization, and then an applied surface current $\myv K = -\myv K_b$. Let's first calculate the field in the solid torus, by way of finding all the (bound) current in the problem.
The magnetization is $\myv M=M\uv \phi$. So the bound surface current is $\myv K_b=\myv M \times \uv n$. Therefore, $K_b=M$ on all the surfaces, and is directed...
- up on the inside surface,
- outwards on the top surface,
- down on the outside,
- inwards on the bottom.
The bound current density is $\myv J_b=\myv \grad \times (M\uv \phi)$. But since $\myv M$ is ~ independent of $s$, the curl vanishes, and there is no bound current density.
To find $\myv B\approx B\uv \phi$, draw an Amperian loop (tangent at all points to $\uv \phi$ in the middle of the torus, such that: $$\begineq \oint_{\cal P}B\,dl&=\mu_0 I_\text{enc}\\ BL&=\mu_0K_bL=\mu_0ML\endeq$$ So, as in the case of the magnetized cylinder, we again have $\myv B= \mu_0\myv M=\mu_0M\uv \phi$.
If we imagine slicing out a wedge of width $w$:
- ...two new flat surfaces, but on the these surfaces, $\myv M \times \uv n=0$ (no surface current),
- We have subtracted a belt of width $w$ girdling the torus where there was a surface current $K=M$ circulating.
So, we can account for all the currents in the problem by adding a girdle of current of width $w$ with surface current density $K=M$ circulating opposite the solid-torus surface current. The resulting field will be in the opposite direction from $\myv M$.
Use the results of problem 5.8 (field at the center of a square loop) to find the field at the center of a square loop with current $I=Kw=Mw$. $$B=\frac{\sqrt 2 \mu_0 I}{\pi(a/2)}=\frac{2\sqrt 2 \mu_0 M w}{\pi a}.$$
Then the field in the middle of the gap will be: $$\myv B=\mu_0\myv M\left( 1-\frac{2\sqrt 2 w}{\pi a}\right).$$
Uniformly magnetized sphere
 Find the magnetic field of a uniformly magnetized sphere.
Find the magnetic field of a uniformly magnetized sphere.
- Let's take the magnetization of the sphere to be $\myv M = M_0\uv{z}$.
- The curl of $\myv M$ is zero, so there's no bound volume charge. We have only a bound surface current
$$\myv K_b = \myv M \times\uv{n} = M_0 \uv{z} \times \uv r = M_0 \sin \theta \uv{\phi}.$$ So, let's use just the bound surface current term of the magnetic potential... $$\begineq\myv A(\myv r) &= \frac{\mu_0}{4\pi}\int_{\cal S}\frac{ \myv K_b(\myv r') }{\rr} da'\\ &=\frac{\mu_0}{4 \pi} \int \frac{M_0 \sin \theta' \uv \phi'}{\rr} da' \\ &=\frac{\mu_0}{4\pi}\int_0^{2\pi}d \phi' \int_0^\pi d \theta' \frac{M_0 \sin \theta' \uv\phi'}{\sqrt{R^2-r^2-2Rrcos \theta'}} R^2 \sin \theta' \\ &=...\endeq$$
Example 5.11 continues this frontal assault on the problem, in which eventually it is found that the field outside the sphere is that of a magnetic dipole, and inside there is a constant magnetic field: $$\myv B = \frac{2}{3}\mu_0 \myv M.$$ But we will shortly see a different way of solving this problem, using the auxiliary field.
Physical picture
For a material with a uniform magnetization, we have $\myv \grad \times \myv M = \myv J_b = 0$. We can think of a slab of material as made up of elementary current loops, all with the same current. At the border of two neighboring loops the current of one cancels the next, so we only have a surface current on the edge of the slab and no "body current" under these conditions.
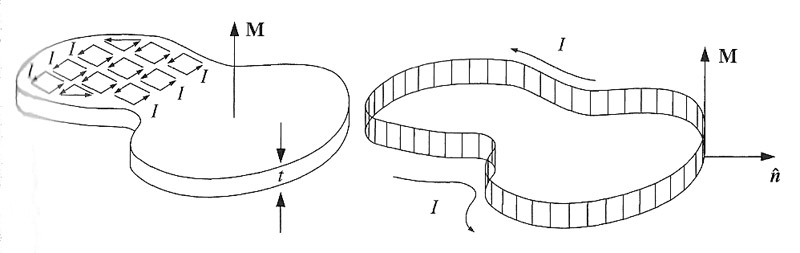
The magnetic moment of one elementary loop is $m = Mat.$
In terms of the current circulating around the loop: $m = Ia.$
$=> I=Mt$.
$=> K_b = I/t = M$.
So $\myv M \times\uv{n}=K_b$ gives the right magnitude for the bound surface current and the right direction.
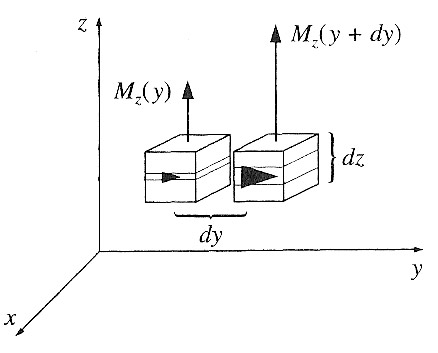 If on the other hand, we have an inhomogeneous magnetization (average magnetic
dipole moment) that is changing, the following picture models things. The current
at the boundary is
If on the other hand, we have an inhomogeneous magnetization (average magnetic
dipole moment) that is changing, the following picture models things. The current
at the boundary is
$$I_x = (M_z(y+dy) - M_z(y))dz = \frac{\del M_z}{\del y}dy dz.$$
And this body free current density is:
$$(J_b)_x = \frac{I_x}{dydz}=\frac{\del M_z}{\del y}$$
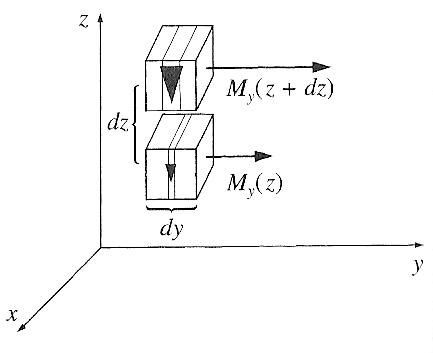 An inhomogeneity of the the magnetization in the $z$-direction will also contribute
to the current density in the $x$-direction, by...
An inhomogeneity of the the magnetization in the $z$-direction will also contribute
to the current density in the $x$-direction, by...
$$(J_b)_x = - \frac{\del M_y}{\del z}.$$
These two equations together are consistent with our expression for the bound volume current density:
$$\myv J_b = \myv \grad \times \myv M.$$