Dielectrics
We've examined electric fields in
- the vacuum with no charges (Laplace's equation holds)
- in conductors with lots of mobile charges ($\myv E=0$)
 Insulators (dielectrics) are one kind of material that we have managed to ignore...up until now.
Insulators (dielectrics) are one kind of material that we have managed to ignore...up until now.
Dielectrics
A.K.A. "Insulators"
Simplified picture of insulators (dielectrics):
- Plenty of charge inside
- But no free charges (no charges that are free to move long distances in response to $\myv E$). Charges are bound (in molecules or on a crystal lattice) much more tightly than in a conductor.
Examples: Air, teflon, calcium carbonate
Induced dipoles (atomic)
When an electric field is applied to something like an atom which is electrically
neutral, but is made up of positive and negative charges, the different charges
move in response to the electric field, resulting in a small dipole moment.
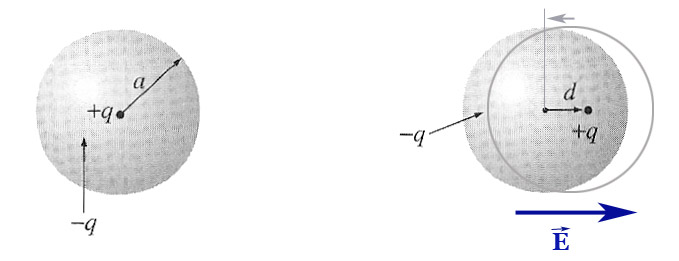
The induced dipole is generally proportional to the applied field (for an isolated atom): $$\myv p = \alpha \myv E.$$
Knowing a little about chemistry... Which bare atom do you think will have the biggest dipole in the same electric field: $H$, $He$, or $Li$?
Values of $\alpha$ for a variety of atoms (units: $\frac {10^{-30}m^3}{4\pi \epsilon_0}$):
| H 0.667 |
He 0.205 |
Li 24.3 |
Be 5.60 |
C 1.76 |
Ne 0.396 |
Na 24.1 |
Ar 1.64 |
K 43.4 |
Cs 59.6 |
Problem 4.4
A point charge $q$ is situated a distance $r$ away from a neutral atom with polarizability $\alpha$. Find the force of attraction between them.
You can:
- Use the electric field of a point charge, to find the field at the polarizable atom, a distance $r$ away.
- Calculate the polarizaton of the atom, $\myv p$. And what direction is it polarized in? (what direction does $\myv p$ point?)
- We calculated the electric field of a dipole as $$\myv E_\text{dipole} = \frac{p}{4\pi \epsilon_0 r^3}(2\cos \theta\uv{r} + \sin \theta \uv{\theta})$$
- So, what is the electric field of the dipole back at the position of the point charge?
- Use $F=qE$ to find the force on the point charge.
The electric field from the point charge is $E=\frac{1}{4\pi \epsilon_0}\frac{q}{r^2}$.
The induced dipole is $\myv p = \alpha \myv E=\frac{1}{4\pi \epsilon_0}\frac{q \alpha}{r^2}$.
We calculated the electric field from a dipole. It was: $$\myv E_\text{dipole} = \frac{p}{4\pi \epsilon_0 r^3}(2\cos \theta\uv{r} + \sin \theta \uv{\theta})$$
Dielectric Breakdown
 But a material is not always a conductor or not always an insulator:
But a material is not always a conductor or not always an insulator:
- Put a high enough $\myv E$ field on normally-insulating air, and electrons are forcibly stripped from atoms ("dielectric breakdown" happens when the electric field strength exceeds $3\times 10^6$ V/m) and you get a conducting soup of ions.
- Dielectric breakdown happens intentionally, and continuously in a fluorescent light.
- In a semiconductor FET (Field Effect Transistor), an applied electric field can switch a region of the semiconducting material from conducting to non-conducting and back.
"Permanent" dipoles (and induced polarization)
Another possibility is that a molecule has a pre-existing, or permanent dipole
moment, such as water. Then, when an electric field is applied, such molecules
will feel a torque turning them somewhat in the direction of
the field:
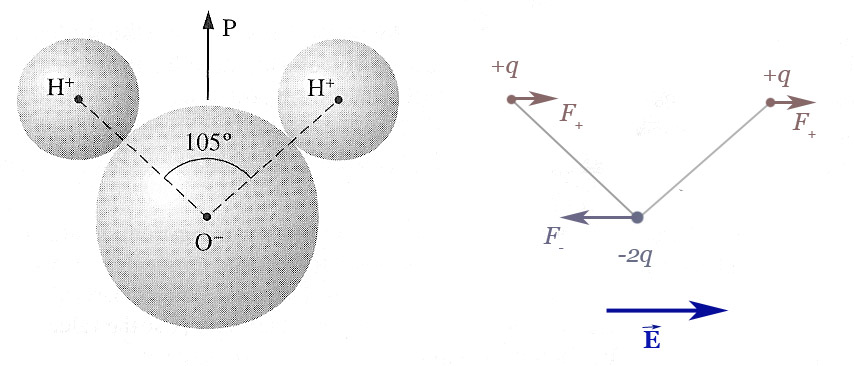
We might expect that the water molecules in a volume of water are equally likely to be pointing in any direction. And thus the average dipole moment of a sample of water is 0.
But applying an electric field could partially align molecular dipoles, giving rise to a non-zero average dipole moment.
One might also imagine what happens in ionic solids...
Whatever the mechanism, the end result is that on the microscopic level, there are dipoles aligned with the field that weren't there before.
Image credits
Ian Boggs, Werl Triptychon by Robert Campin (1438).