[11.7] - Triple integrals / Volume
- Find the volume of the figures shown below, using both a triple integral, and geometry.
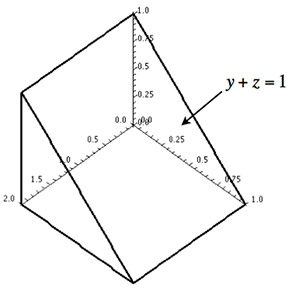
By geometry $V=\frac12*(2\times1\times1)=1$;
Setting up the integral... $$\begineq\int_{x=0}^2\int_{y=0}^1\int_{z=0}^{1-y} dz\,dy\,dx &=\int_{x=0}^2\int_{y=0}^1(1-y) \,dy\,dx\\ &=\int_{x=0}^2 \left[y-\frac{y^2}2\right]_{y=0}^1\\ &=\int_{x=0}^2 1-\frac 12=\left[\frac12x\right]_{x=0}^2 = \color{blue}1 \endeq$$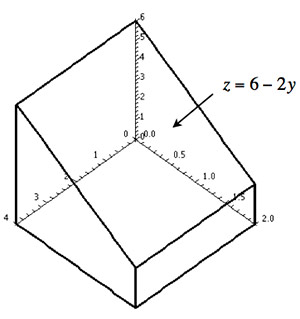
By geometry $V=4\times2\times2+4\times2\times\frac12\times4=32$
-
Sketch the solid whose volume is given by
$$\int_0^4\int_0^{\frac{4-x}{2}} \int_0^{\frac{12-3x-6y}{4}} dz\,dy\,dx$$
The upper limit for the $z$ integral is $z=\frac14(12-3x-6y)$. This is the equation of a plane. It intersects the $x$-axis at $(x,0,0)$. Plugging these coordinates into the equation of the plane, we get: $$0=\frac14(12-3x).$$ This means $\color{blue}x=4$. In a similar manner, we find that the plane intersects the $y$-axis at $\color{blue}y=2$ and the $z$-axis at ${\color{blue}z}=\frac{12}{4}\color{blue}=3$.
The solid is a tetrahedron, occupying the volume underneath the plane $z=\frac14(12-3x-6y)$ in the first quadrant:

Then rewrite the integral in the order $\int \int \int dy\,dx\,dz$ with the appropriate limits of integration.
From our sketch, the limits on the outermost integral will be $\color{blue}0\lt z\lt3$.
For each $z$ value, we'll integrate (2nd) from $x=0$ to some $x(z)$, which will be the intersection of our plane with the $x-z$ plane, which is same as the $y=0$ plane. Plugging $y=0$ into the equation of the plane we get: $z=\frac14(12-3x-6\cdot 0)$.
Solving this for $x(z)$, $\color{blue}0\lt x\lt 4-\frac43z$.
Finally, to get the upper limit on the $y$ integral, we want to integrate from some point in the $x-z$ plane "up" to the our plane, written as a function $y(x,z)$. Solve our original function for the plane, $z=\frac14(12-3x-6y)$ for $y$, we find that the upper limit is $y(x,z)=\color{blue}\frac16(12-3x-4z)$. Putting these all together: $$\color{blue}V=\int_{z=0}^3\int_{x=0}^{4-\frac43z}\int_{y=0}^{\frac16(12-3x-4z)}\,dy\,dx\,dz$$
-
Find the volume of the tetrahedron bounded by the coordinate plane
$z=4-4x-2y$.
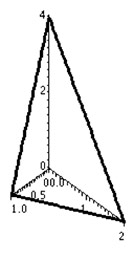
The line in the x-y plane is $y(x)=2-2x$. We could iterate $0\lt x\lt 1$, then $0\lt y \lt 2-2x$, then $0\lt z \lt 4-4x-2y$: $$\begineq V=\iiint dV&=\iiint dx\,dy\,dz\\ =& \int_{x=0}^1\int_0^{y=2-2x}\int_0^{z=4-4x-2y}dz\,dy\,dx\\ =& \int_{x=0}^1\int_0^{y=2-2x}(4-4x-2y)\,dy\,dx\\ =&...=\color{blue}\frac43 \endeq $$
Check your answers to these last 2 using the formula for the volume of a trirectangular tetrahedron:
A trirectangular tetrahedron has 3 legs which meet at right angles at one point. If the lengths of these legs are $a$, $b$, and $c$, then the volume of the tetrahedron is: $$V=\frac {abc}6.\nonumber$$
-
Find the volume of the tetrahedron shown below.
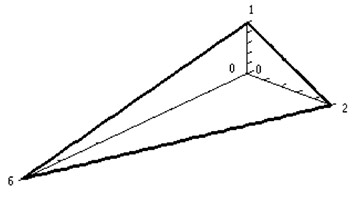
To be different, start by iterating $0\lt y \lt 2$. Then that line in the $x-y$ plane is given by $x(y)=6-3y$ (Check that this line runs through (6,0) and (0,2)).
What's the equation of the plane? The intersection of the plane with the $x-y$ plane (the $z=0$ plane) is $x=6-3y$ This implies $0=6-3y-x$. So, if we set $z=a(6-3y-x)$ we're guaranteed to intersect the $x-y$ plane along the line $6-3y-x=0$ when $z=0$.
We'd like the plane to intersect the point (0,0,1). Plugging this point in to $z=a(6-3y-x)$ gives us $1=6a$, So choose $a=\frac 16$. So the plane is $z=\frac16(6-3y-x)=1-\frac y2 -\frac x6$.
So, the integral to solve is: $$ V=\int_{y=0}^2\int_{x=0}^{x=6-3y}\int_{0}^{z=1-\frac y2 -\frac x6} \,dz\,dx\,dy $$ Using the trirectangular volume formula, the answer should be $V=\frac{6*2*1}6=\color{blue}2$.