[11.5] - Double Integrals in Polar Coordinates
- Integrate $f(x,y)=x^2+y^2$ over the domain $D=\{(x,y):1\leq (x^2+y^2)\leq 4
\}$ using polar coordinates.
-
Sketch the region of integration and evaluate by changing to polar coordinates.
$$ \int_0^3\int_{x=0}^{\sqrt{9-y^2}}\sqrt{x^2+y^2}\,dx\,dy$$
-
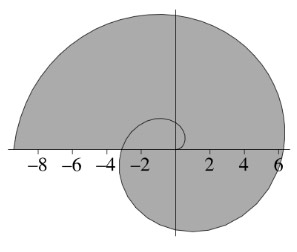 Find the shaded area of the region inside the curve $r=\theta$, $0\leq \theta \leq 3\pi$. Hint:
Make sure you're not double-counting any areas.
Find the shaded area of the region inside the curve $r=\theta$, $0\leq \theta \leq 3\pi$. Hint:
Make sure you're not double-counting any areas.
-
Rewrite $\int_{-2}^2\int_{y=0}^{\sqrt{4-x^2}}e^{-x^2-y^2}\,dy\,dx$ as a polar integral, and evaluate it.
Answers
show / hide
-
$$\iint r^2\,dA=
\int_{\theta=0}^{2\pi}\int_{r=1}^2 r^2\,r\,dr\,d\theta=\int_{\theta=0}^{2\pi}\left(
\left.\frac{r^4}{4}\right|_1^2\right)\,d\theta=
\frac{15\pi}{2}$$
-
$$\int_0^{\pi/2}\int_0^3 r(r\,dr\,d\theta)=\frac{9\pi}{2}$$
- The equation of the black line is $r(\theta)=\theta$.
$$\iint\,dA=\int_{\theta=\pi}^{3\pi}\int_{r=0}^\theta r\,dr\,d\theta
=\frac{13\pi^3}3
$$
- By hand, you should evaluate the $\int dr$ integral first to bring down the $\theta$ dependent limit before you integrate wrt $\theta$.
- To avoid double-counting areas, the lower limit on $\theta$ should be $\pi$ (not 0, even though the black line starts at $\theta=0$).
- $$\int_{\theta=0}^\pi\int_{r=0}^2 e^{-r^2}r\,dr\,d\theta = \frac\pi2
\left(1-\frac1{e^4}\right)$$
 Find the shaded area of the region inside the curve $r=\theta$, $0\leq \theta \leq 3\pi$. Hint:
Make sure you're not double-counting any areas.
Find the shaded area of the region inside the curve $r=\theta$, $0\leq \theta \leq 3\pi$. Hint:
Make sure you're not double-counting any areas.