Assignments: 1 | 2 | 3 | 4 | 5 | 6 | 7
Homework / Assignments
Work these problems to learn the material. I encourage you to work with others to develop approaches to solving these. Consult with me too.
Since Carter has many answers in the back of the book, you must show your work to receive credit for your answers.
There is a set of worked solutions to Carter's problems online. You may check your work against their worked solutions. Of course you will most likely learn more by trying to develop an approach on your own or with each other, before consulting these solutions.
You will not hand in your homework. But I'll quiz you on the problems assigned.
Assignment #5
Carter
Chapter 5: Chapter 5:
5, 6, 8, 10, 13
Meyer-Reimer: Heat pump/furnace comparison (Hand it in on Moodle separately.)
Notes/Answers
Carter, Chapter 5
Problem 5 (5-5)
The internal energy of an ideal gas depends only on temperature, and an expression is given in problem 5-2. The enthalpy of an ideal gas is also a function of temperature alone...
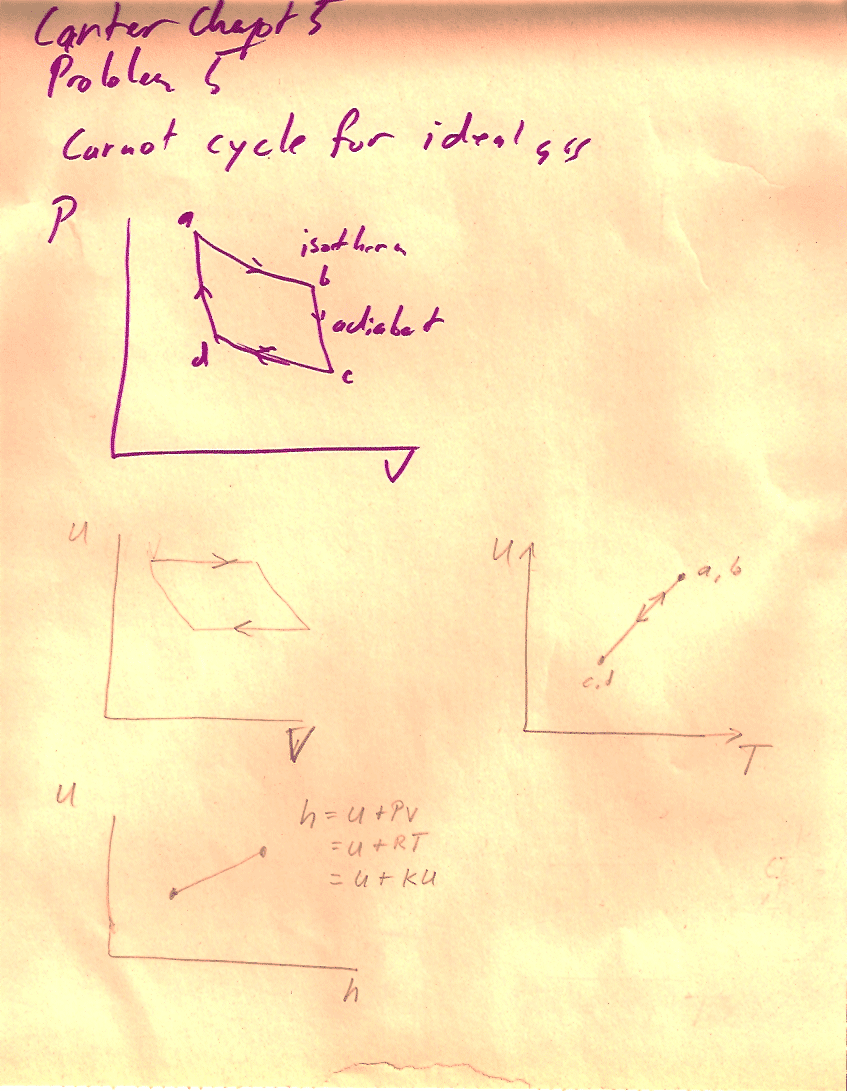

Carter, Chapter 5
Problem 6
Carter, Chapter 5
Problem 7

Carter, Chapter 5
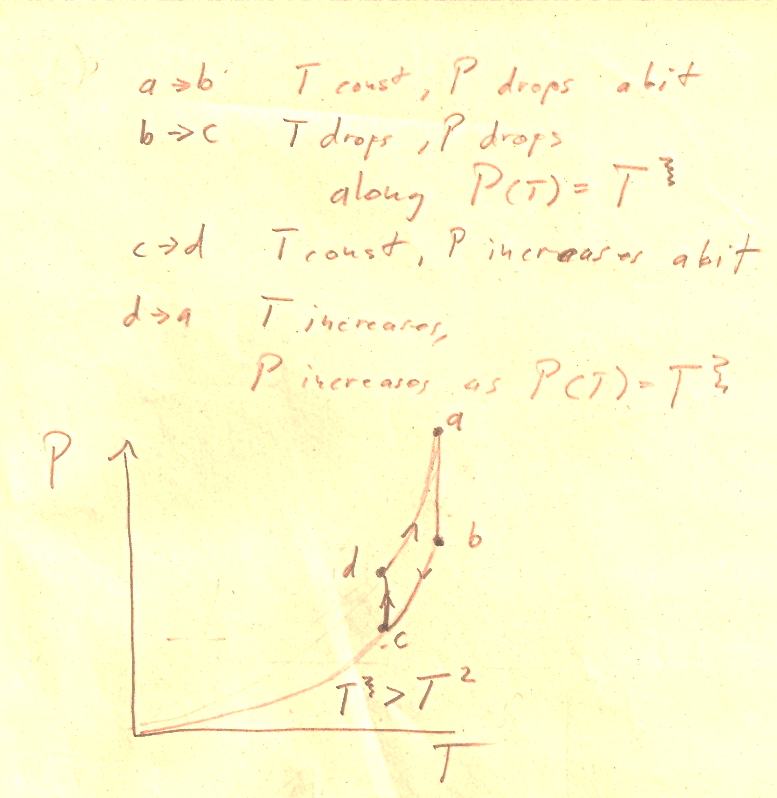
Problem 8

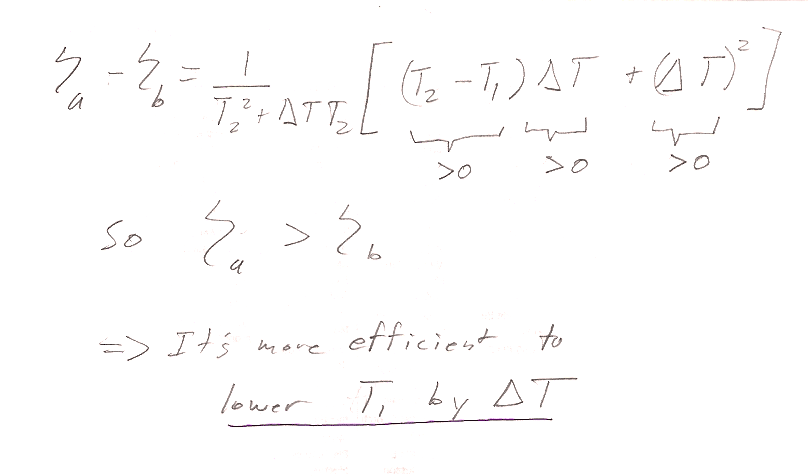
Or, just plug in some numbers, and calculate efficiencies for the two cases.
Carter Chapter 5
Problem 10
This is not a Carnot cycle, so you cannot use $\eta=1-T_1/T_2$. The more general definition is $\eta =$(work out)/(heat in):
In the Carnot engine, heat enters the system in only one of the 4 processes that makes up the cycle. The sneaky thing with this machine is that heat is entering the system on cycles 1$\to$2 and 2$\to$3. So when you calculate efficiency: $$\eta=\frac{W}{Q_{\text{in}}} = \frac{W}{Q_{1\to 2}+Q_{2\to 3}}$$

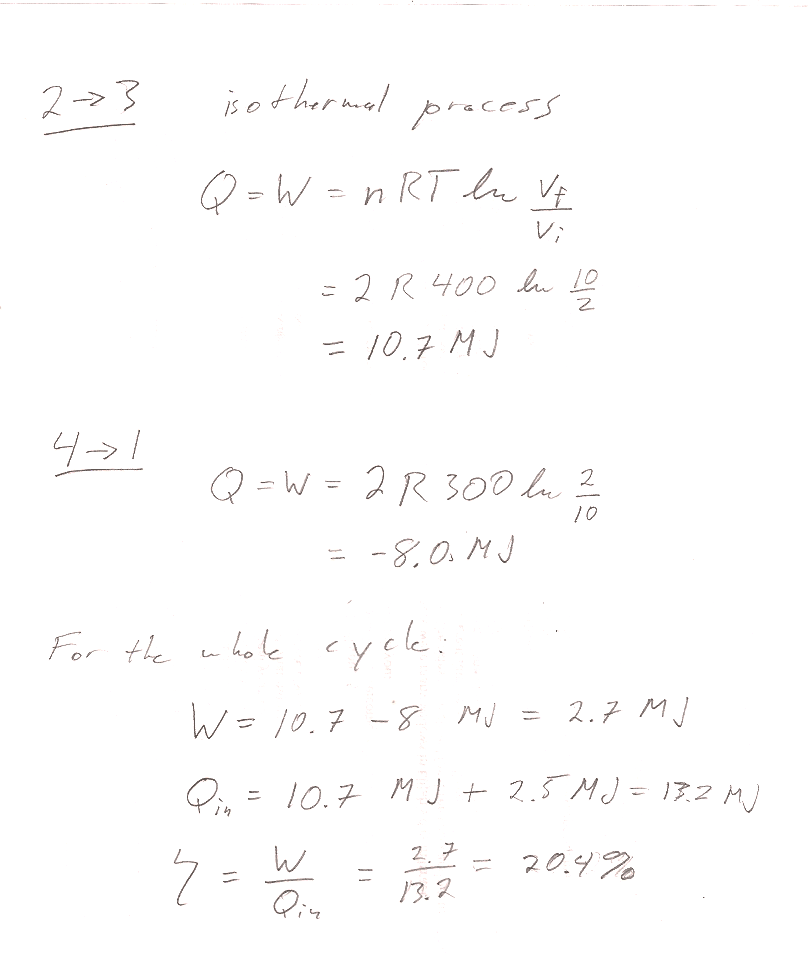
Carter Chapter 5
Problem 13
In the first part, I am looking for some explicit recognition of "What we get" and "What we pay". Are they heats or works? From which part of the cycle?
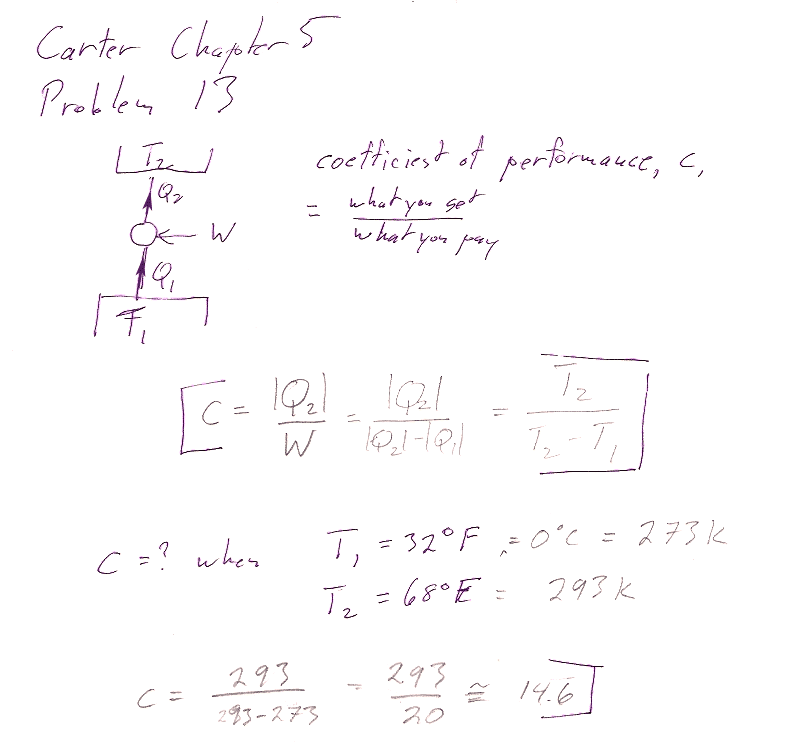
Assignment #6
Chapter 6: 1, 2, 3, 6, 12, 13Notes/Answers
Carter Chapter 6
Problem 1
6.1: From the info given, you should be able to find the ratio $T_1/T_2$ readily. Equations 5.17 and 5.18 are relationships between volumes and temperatures for an adiabatic process. You can, for example, solve 5.17 (and 5.18) to get the ratio $v_b/v_c$ (and $v_a/v_d$) in terms of the ratio of $T_1/T_2$ and $\gamma$. You also are given the overall ratio of $v_c/v_a$...
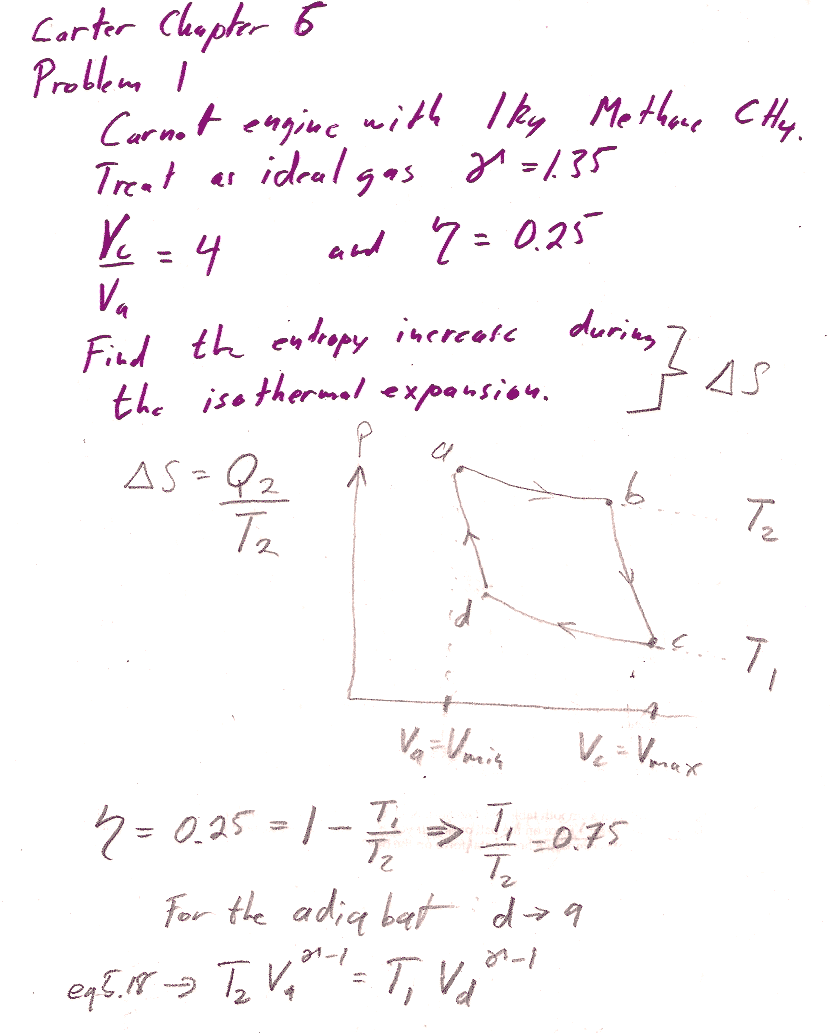
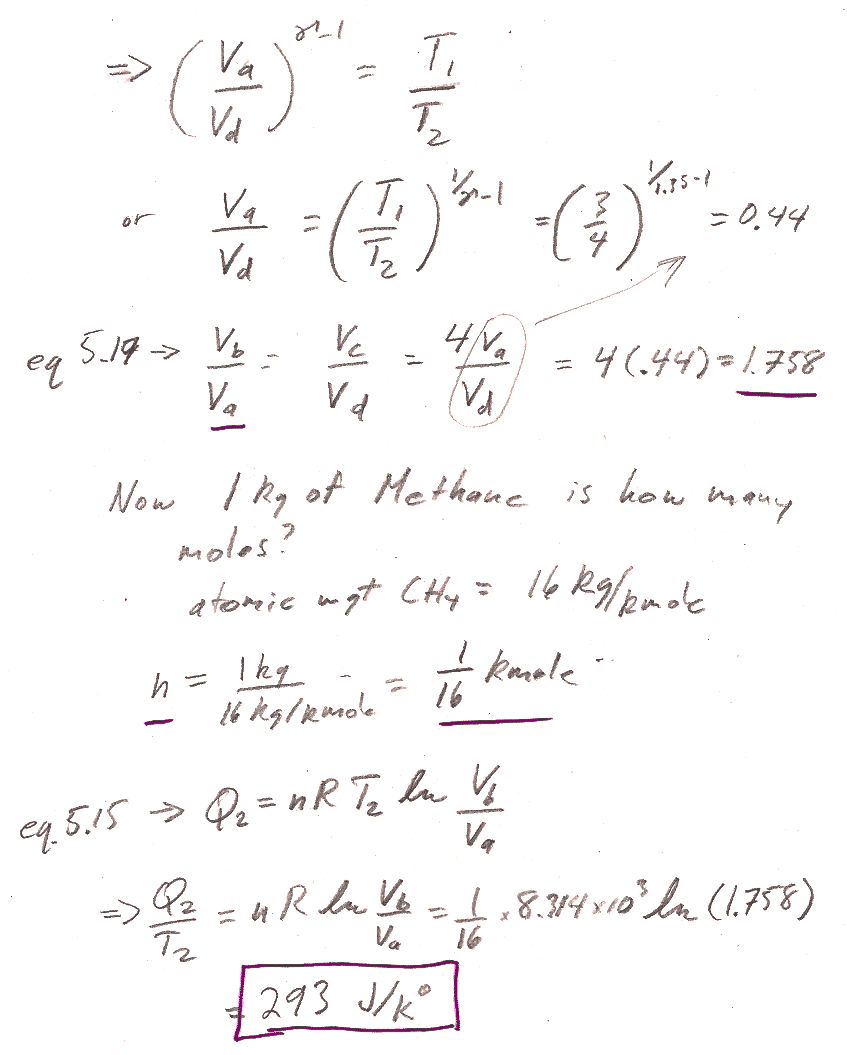
Carter Chapter 6
Problem 2
a.) I did not get the answer in the back of the book: I calculated $\Delta S=779$ J/K.
I did manage to get the answer in the back of the book if I convert 80 C to 353 K and 20 C to 273 K, (should be 293 K), so I think that's an error on their part.
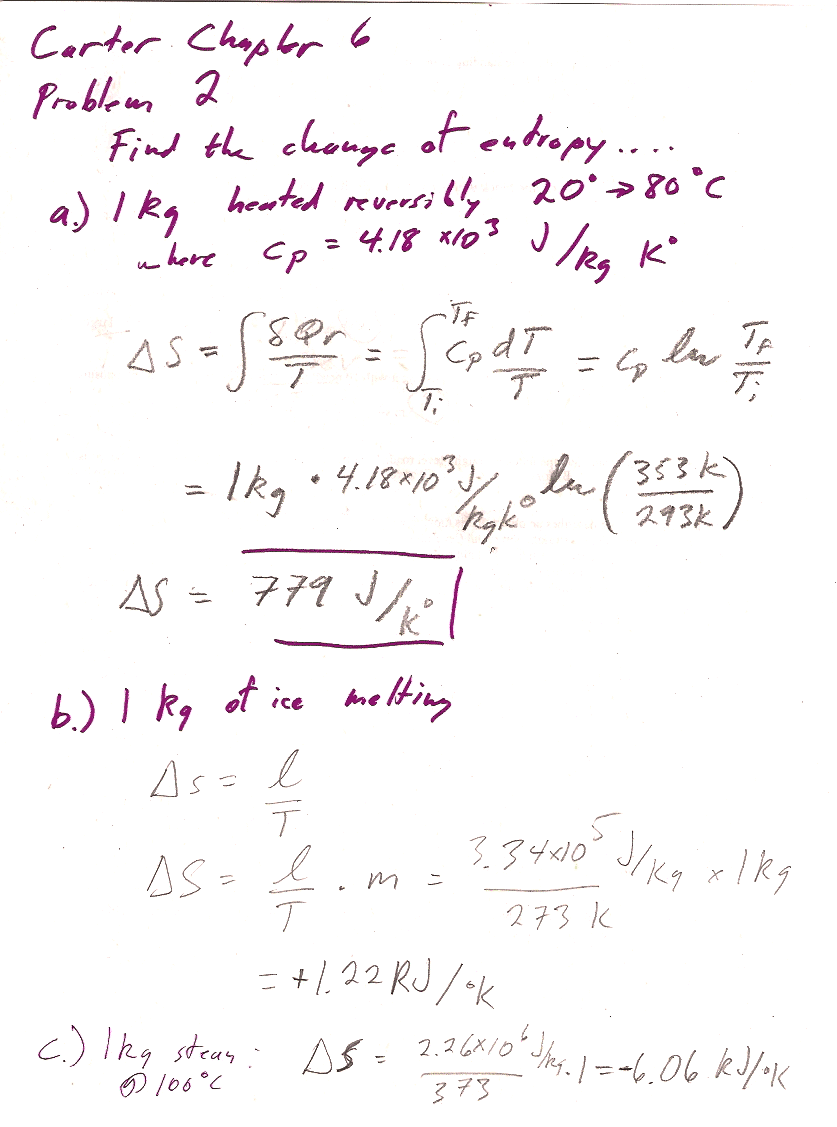
Common issue: during condensation $\Delta Q \lt 0$, heat is leaving the system, so the entropy change is *negative*.
Carter Chapter 6
Problem 3
First Law, for reversible processes: $$dU=\delta Q_r+PdV$$ So, if $dV=0$ (isochoric process) $(dU)_V=\delta Q_r$. This implies that: $$\left(\frac{dU}{dT}\right)_V = \left(\frac{\delta Q_r}{dT}\right)_V =C_v.$$ Or, $(\delta Q_r)_V=C_V\,dT$, where $C_v$ might be a function of temperature, $T$.
It looks to me like Carter has mixed up moles or kilomoles somewhere, or else Joules and kiloJoules. I calculate his answer to be off by exactly 3 orders of magnitude. When I carried out the integration, I found a total entropy change for 1 g of diamond of $\Delta S= 0.127$ J/K The heat capacity of diamond is 0.015
Entropy change of 1 g of Diamond heated at constant volume from 4 K to 300 K with $$c_v=1.88\times 10^6\left(\frac{T}{\Theta}\right)^3$$ units are Joules/kilomole/${}^o$K, and $\Theta=$2230 K.
The molecular weight of diamond is 12 g / mole, so 1 g = 1/12 mole = $8.3\times 10^{-5}$ kilomoles = $n$.
$$dS = n \delta q_r / T$$ Integrating... $$\begineq \Delta S&= \int dS = \int n \frac{\delta q_r}{T} = \int n \frac{c_v\,dT}{T}\\ &= \int_{4 K}^{300 K}n 1.88\times 10^6 \frac{T^2}{\Theta^3} dT\\ &= \frac{n 1.88\times 10^6}{\Theta^3} \left[T^3/3\right]_{4}^{300}\\ &= \frac{8.3\times 10^{-5}*1.88\times 10^6}{3*2230^3} \left(300^3-4^3\right)\\ &= 0.127 \ {\text J/K}\endeq$$
Carter Chapter 6
Problem 6
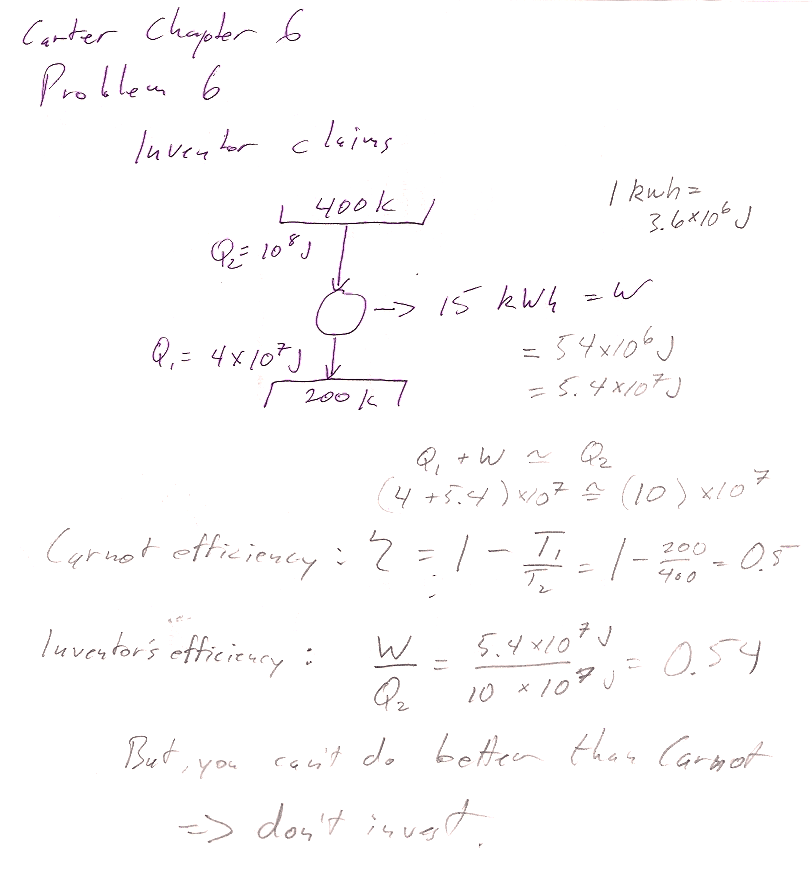
Carter Chapter 6
Problem 12
I was looking for some explicit acknowledgement that the 2nd law means that the entropy of the universe has to increase (or stay the same) with each process. So, even if $\Delta S_{system}<0$, as long as $\Delta S_{surroundings}$ is positive, and greater than $|\Delta S_{system}|$, then the net change of entropy $$\Delta S_{universe}=\Delta S_{sys}+\Delta S_{sur}$$ will still be $\geq 0$.
Carter Chapter 6
Problem 13
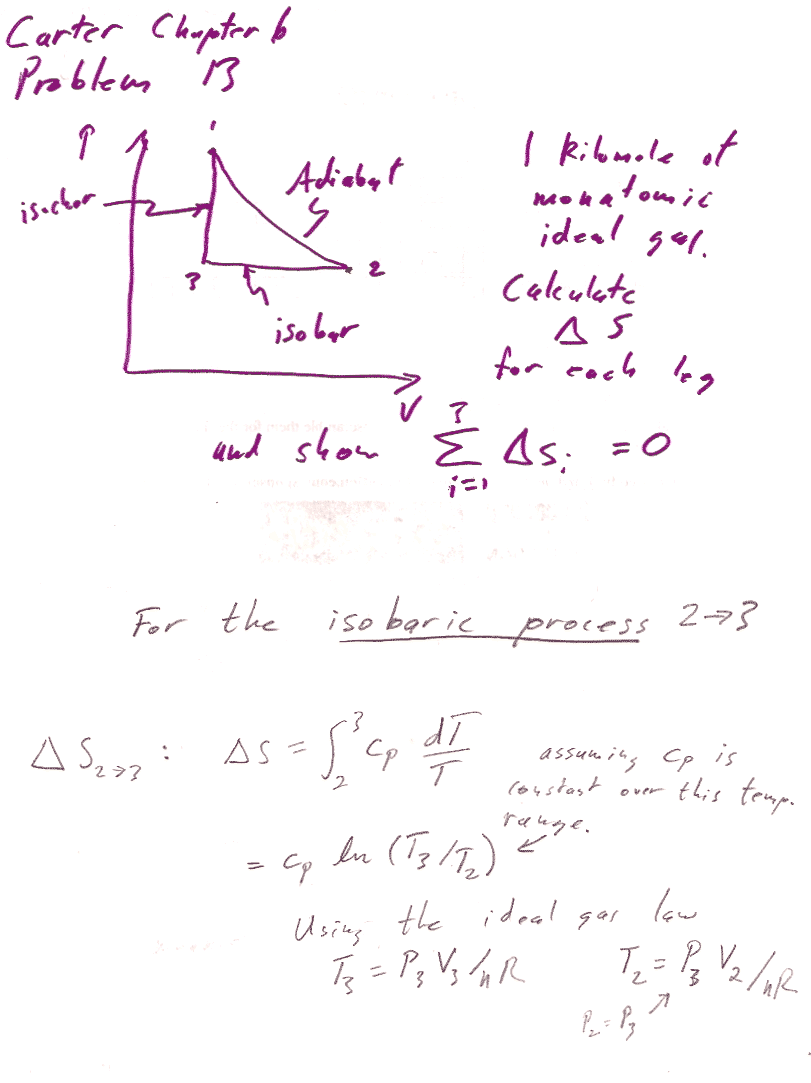
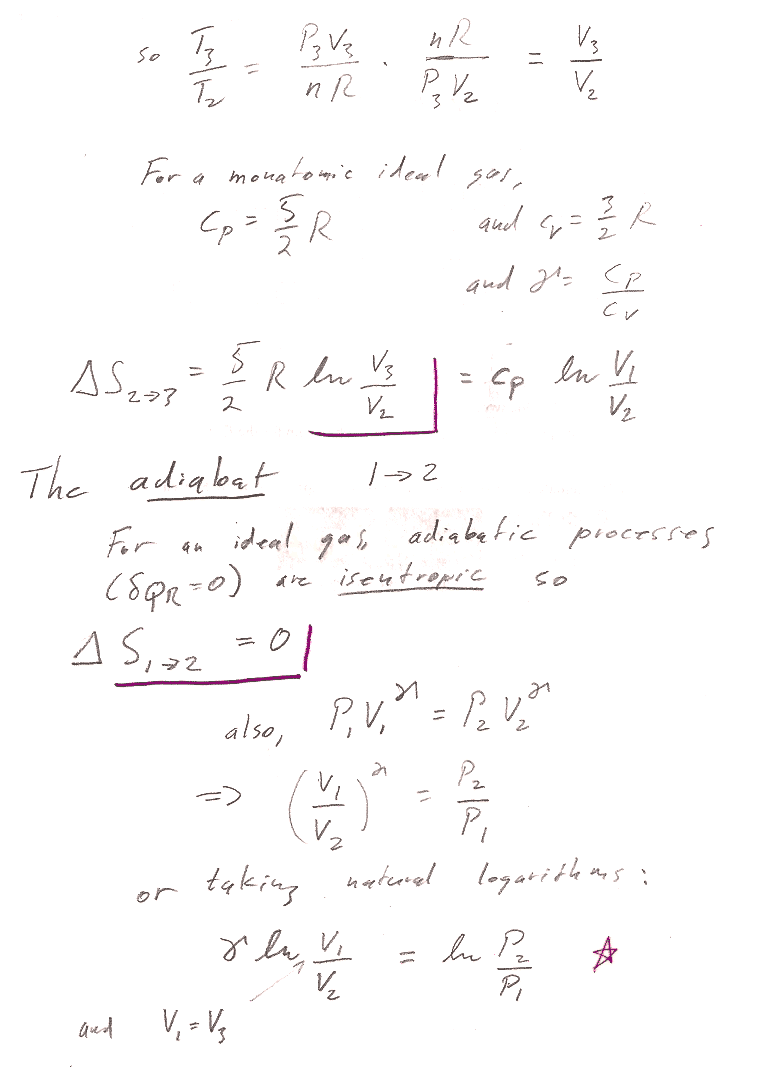

This last step is a result of Mayer's equation--one expression of this is that $\gamma=c_P/c_V$.
This calculation shows that the entropy change for the whole cycle is 0, but you could also calculate explicit numbers for each part of the cycle.... like this:
2$\to$3 is an isobaric process with initial volume 4 m^3 and final volume 2 m^3. $C_P=n*c_P=1*(5/2)*R$: $$\Delta S_{2\to 3} = \int\frac{\delta Q_r}{T}=\int\frac{C_P\,dT}{T}$$ For a constant pressure process, differentiating the ideal gas law gives $$P\,dV=nR\,dT$$ or, $dT=\frac{P}{nR}dV$. Substituting into the express for entropy... $$\begineq\Delta S_{2\to 3} &= \int\frac{C_PP\,dV}{nRT}=\int\frac{C_P\,dV}{V}\\ &=C_P\ln{V_f}{V_i}=(5/2)*R\ln{2/4}=-14,071 J/K\endeq $$ For the isochoric process $3\to 1$, $$\Delta S_{3\to 1}=\int\frac{\delta Q_r}{T}=\int\frac{C_vdT}{T}=C_v\ln{T_1/T_3}$$
We already showed that, for the adiabatic process, $\Delta S_{1\to 2}=0$. So, the total change in entropy change for the cycle is: $$\Delta S= \Delta S_{1\to 2} + \Delta S_{2\to 3} +\Delta S_{3\to 1}=0$$
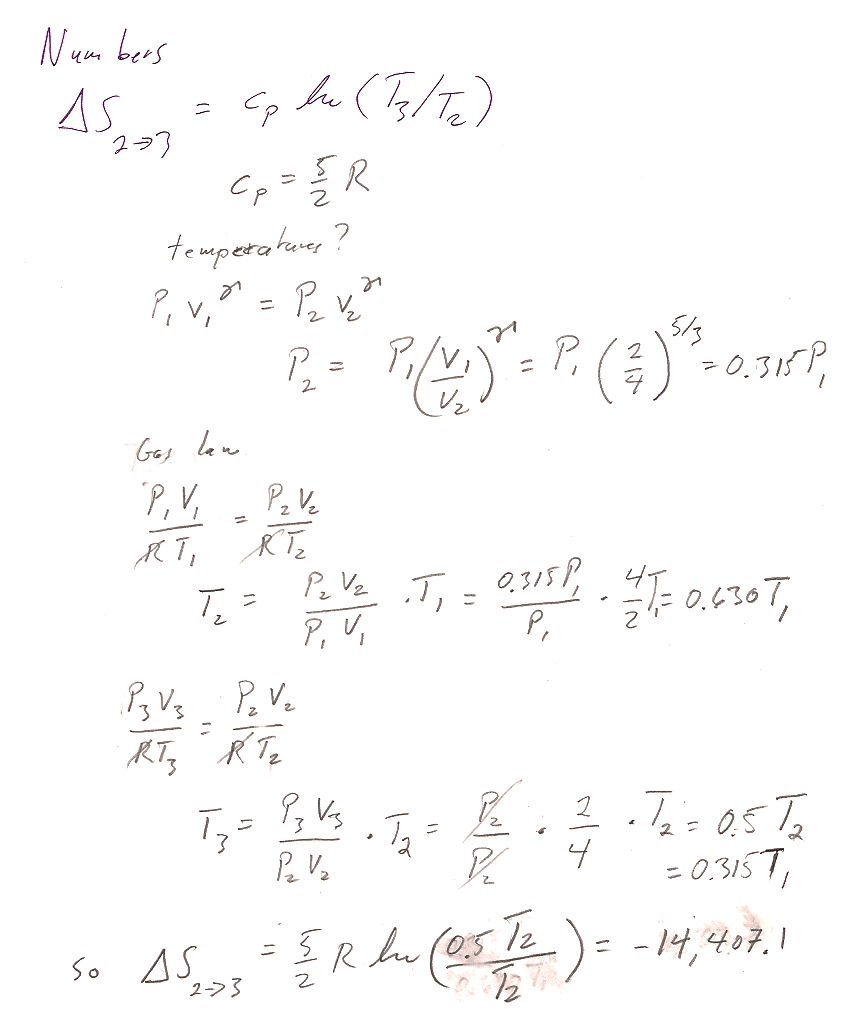
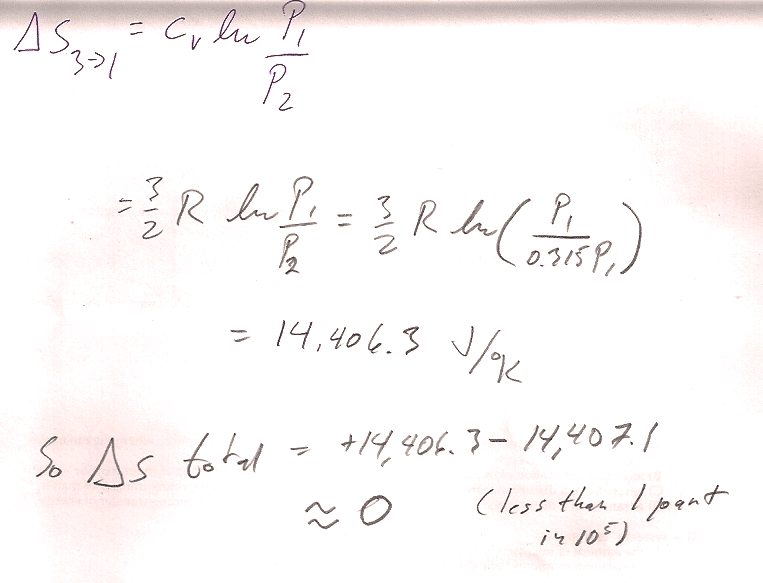
The pressures, temps, etc. were:
- Two volumes are given, and since one of the processes is isochoric: $$V_1= V_3=2\text{ m}^3;\ \ V_2=4\text{ m}^3.$$
- The two points on the adiabat are related by $P_1V_1^\gamma=P_2V_2^\gamma$, so $$P_2=P_1(V_1/V_2)^\gamma=10 \text{ atm }*(2/4)^{5/3}=3.15\text{ atm}; \ \ P_3=P_2$$
- Using the ideal gas law, $T=PV/R$ (and multiplying pressures in atm by $1.013\times10^5$ Pa/atm so as to get temperatures in degrees K): $$T_1=244.17 K;\ \ T_2=153.83 K;\ \ T_3=76.91 K.$$
Assignment #7
Carter
Chapter 7: 2, 3ab, 5, 8
Chapter 8: 1, 3, 6
Notes
Carter Chapter 7
Problem 2
Read section 7.8 in Carter.
My answer was $$\color{blue}\Delta S_\text{universe}=+704.7 \text{ J/K}$$ using the value in the problem of 334.8 kJ/kg for the heat of fusion of water. But online, I see values of this ranging from as low as 333 kJ/kg. A lower value gets closer to the book's answer.
Let's break the cooling into three parts:
- 10 kg of water cools from 20 C (=293 K) to 0 C (=273 K) at constant pressure.
Water loses an amount of heat $$\Delta Q=\int \delta q =\int mc_p\,dT = mc_p\Delta T$$ So, the change in entropy of the reservoir, which is at -10 C (263 K) is... $$\Delta S_{res}=\Delta Q/T_{res}= 10*4180*20/263= +3,178.7\ J/K.$$ For the water, the differential of entropy, under constant pressure conditions is $$ds=\frac{\delta q}{T}= \frac{mc_P\,dT}{T}$$ Integrating this gives $\Delta S=mc_P\ln(T_f/T_i)$, so $$\Delta S_{H_2O}=10*4180*\ln(273/293)=-2,955.3\ J/K.$$
- Water at 0 C loses heat (10 kg)(3.35$\times 10^5$ J/kg)=3.35 MJ. The decrease in entropy of the water is
$$\Delta S_{H_2O}=-3.35 MJ/273 K = -12,271.1\ J/K.$$
The increase of the entropy of the reservoir is
$$\Delta S_{res}=3.35 MJ/263 K=+12,737.6\ J/K.$$
- Water cools from 0 C (=273 K) to -10 C (=263 K) at constant pressure.
Water loses an amount of heat $mc_p\Delta T$, So, the change in entropy of the reservoir, which is at -10 C (263) is... $$\Delta S_{res}=\Delta Q/T_{res}= 10*2090*10/263=+794.7 J/K.$$ For the water, $$\Delta S_{H_2O}=mc_P\ln(T_f/T_i)=10*2090*\ln(263/273)=-779.9 J/K$$
Adding all six of these $\Delta S$ values together... $$\Delta S_{universe}= +704.7\ J/K.$$
This is different from the book's answer of +660 J/K.
If you use $3.34\times 10^5$ J/kg (instead of $3.35\times 10^5$...) for the heat of fusion of ice then you get 667 J/K...
Notice that at each stage, the net entropy change is positive, i.e. each process is spontaneous.
[Most common problem was not using 263 for the temperature at which heat is entering the ice reservoir.]
Carter Chapter 7
Problem 3ab [8]
See example 3 in the textbook. Note that the heat capacity given is *the total heat capacity* (not heat capacity per kg, not heat capacity per kmole).
You should be able to re-produce the answer in the back of the book (6.3 J/K) if you take the book at its word that the heat capacity--that is the total heat capacity, not the heat capacity/kg--is 150 J/K (and Carter didn't accidentally miss the "per kg" piece of things).
If you did assume that this is a heat capacity/kg, then you multiply by 0.4 and get an answer of ~2.5 J/K.
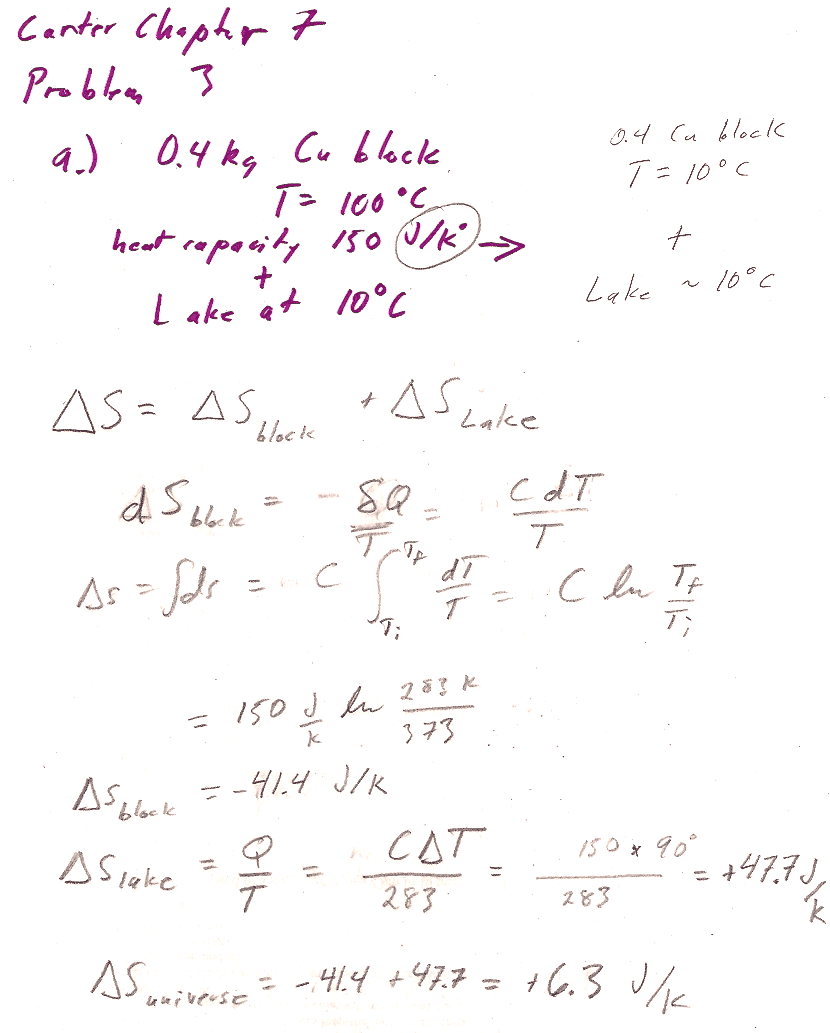

Carter Chapter 7
Problem 5 [6]
For part b, what kind of system boundary have we considered for "free expansion"?
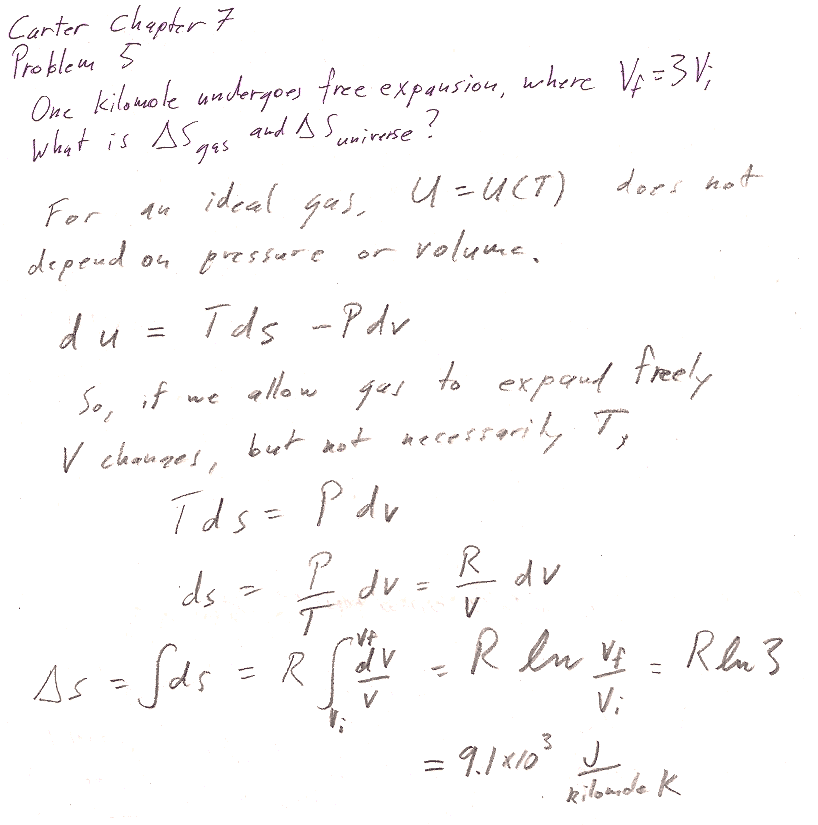
Why is $\Delta S_\text{surroundings}=0$?

Carter Chapter 7
Problem 8
a.) An outline of one possible way to do this problem is in the $T\,dS$ notes.
b.) You may do this analytically (as the textbook suggests) or graphically (by graphing (e.g. hold $T_1$ at some constant temperature, and vary $T_2$ both above and below $T_1$.)
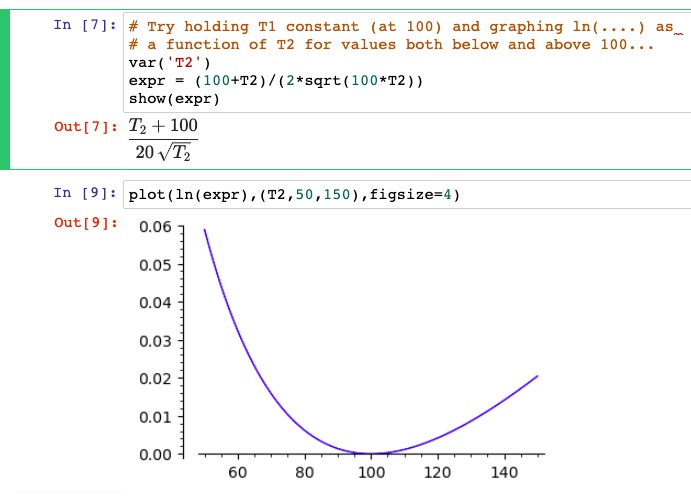
Holding $T1=100$ Kelvin, we see that the log term is greater than zero (means $\Delta S \gt 0$ for all $T2$'s, except $T1=T2$, where it's 0 (mixing two containers of water at the same initial temperature.)
Carter Chapter 8
Problem 1
Problems 1, 3, and 6 all use Maxwell relations.
Hint: You're looking for a partial derivative: The rate of change of entropy with respect to which variable? While which other variable is held constant? Write down the desired partial derivative, and then find a Maxwell relation that lets you calculate it from the equation of state (which links $P$, $V$, and $T$) of the ideal gas; and then of the van der Waals gas.
[I found that the rate of change of entropy with volume (constant T) is greater for a van der Waals gas than for an ideal gas.
You could start from the $Tds$ equation...
$$Tds = c_v\,dT+T\left(\frac{\partial P}{\partial T}\right)_v dv.$$
Setting $dT=0$, and dividing by $T$:
$$ds = \left(\frac{\partial P}{\partial T}\right)_v dv.$$
Or you can get the same relationship using Maxwell relations...
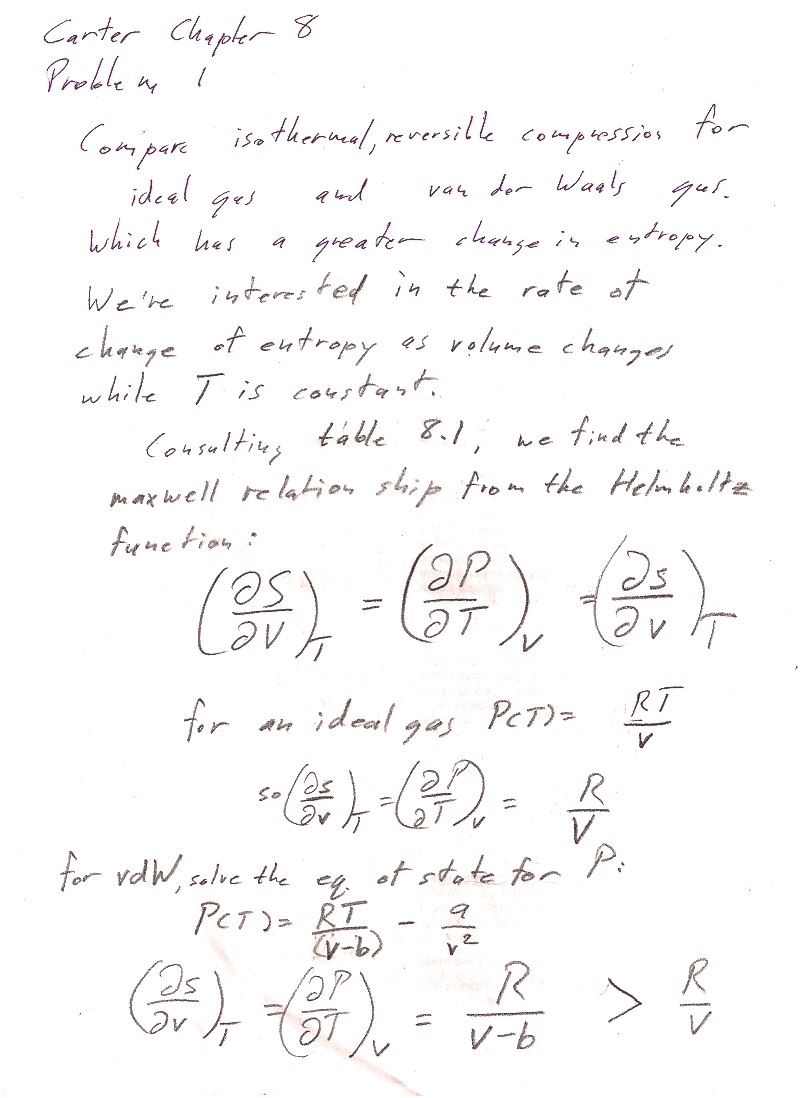
You can see that the rate of change is larger for the VdW gas, if you consider b=0.2v, then $1/(v-b)=1/v*(1/.8)$ which is larger than $1/v$.
*or* several of you integrated these expressions to get:
$$\Delta S_\text{VdW}=R\ln\frac{v_f-b}{v_i-b};\ \ \ \Delta S_\text{ideal}=R\ln\frac{v_f}{v_i}.$$
Put some numbers in, say $v_i=2$, $v_f=1$, and $b=0.3v_i$. The fractions in the logarithms are
$$\frac{1-.3}{2-.3}=\frac{.7}{1.7}=0.412;\ \ \ \frac{v_f}{v_i}=\frac12=0.500.$$
The fraction for the VdW gas is clearly a smaller number than the fraction for the ideal gas.
HOWEVER, the entropy change for each gas is proportional to the natural log of each fraction, and you will see that...
$$\ln(0.412)=-0.89;\ \ \ \ln(0.5)=-0.69.$$
So, the entropy change for the VdW gas is actually larger than that of the ideal gas.
The natural log measures the ratio of how different a number is compared to 1, and *not* how much greater a number is than zero.
This plot shows the two functions to be integrated. $\color{blue}\text{blue for VdW: }1/(v-b)$, and $\color{red}\text{red for ideal gas: }1/v$
Carter Chapter 8
Problem 3
In general (table 8-1), $dF=-SdT-PdV$. Is this perhaps an isothermal process? If you can make the case that it is, then you can use the simpler expression, $$[dF]_T=-PdV$$.
The general expression for the differential of Helmholtz energy is (Table 8.1): $$dF=-SdT-PdV.$$ In this case, the system is in diathermal contact with a reservoir at 0 C. So this process will take place at a constant temperature of 0C = 273 K. Constant temperature means $dT=0$, so $$[dF]_T=-PdV.$$ (2 points for this justification)
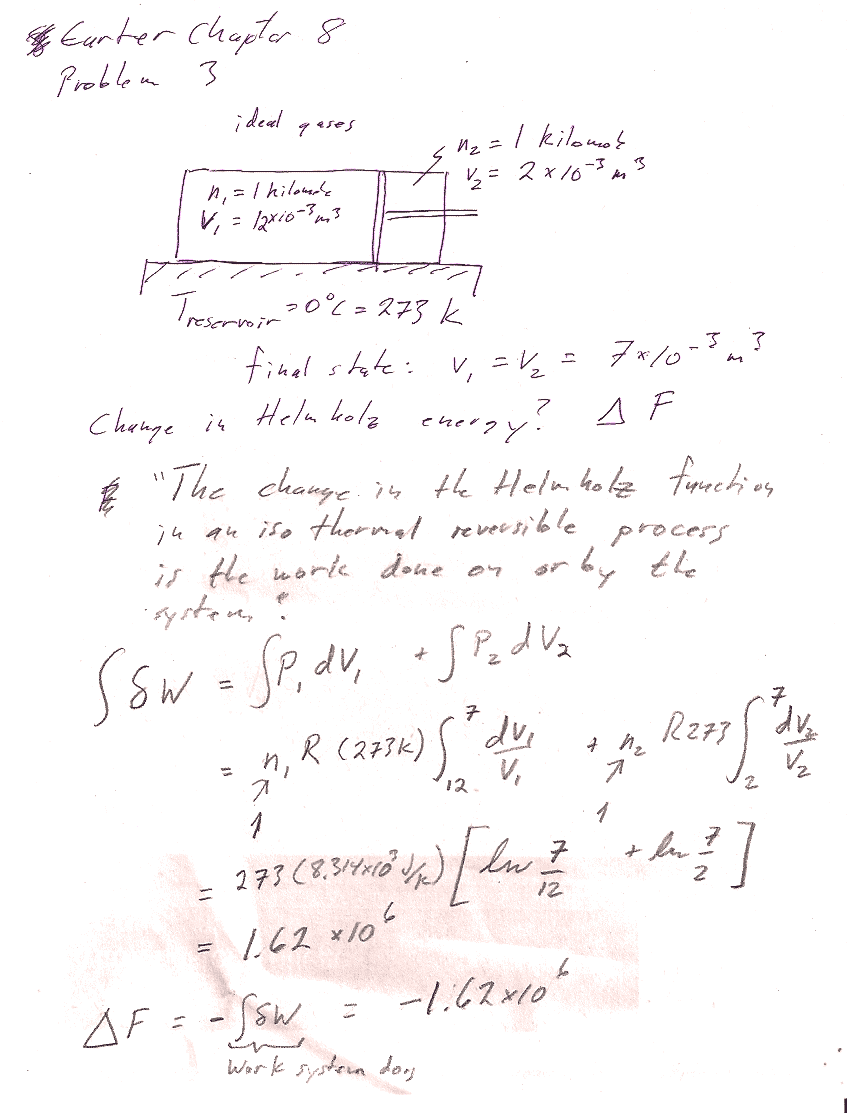
Carter Chapter 8
Problem 6
8.6 - an equation of state is any equation that relates the three thermodynamic parameters $P$, $v$, and $T$ to each other. How can you get $v$ given that you have an equation for $g$? (See our good old table 8-1.)
Carter's answer is not an equation, but it turns out that if you multiply your $V$ by $P$ it should be equal to Carter's answer. Why would he do that?? Notice that the equation you get looks like a "tweaked" ideal gas law: $$PV=nRT+\text{some other terms...}$$ This is an expansion of the ideal gas law in powers of $P$ that might mathematically capture some of the departures of a real gas from the ideal gas law.
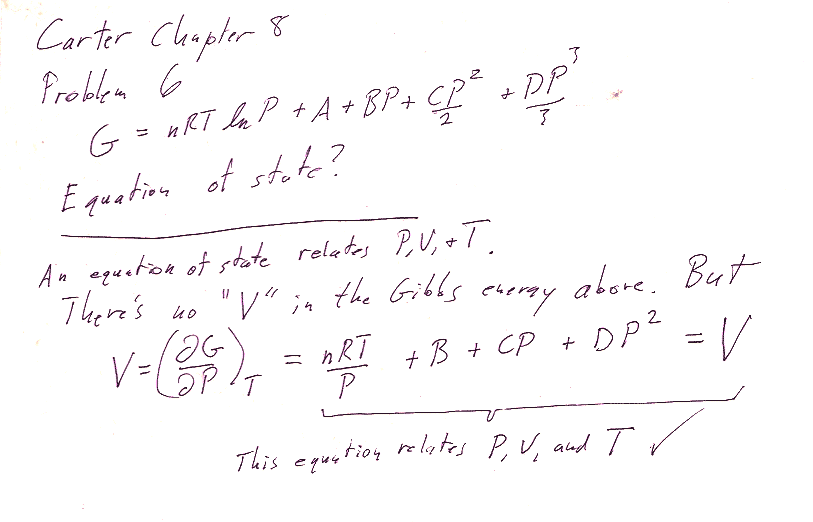
Notice that if you multiply $V$ by $P$ you get: $$PV=nRT + BP+CP^2+DP^3$$ which looks like the ideal gas law ($PV=nRT$) plus some higher order terms in powers of $P$: Sort of a polynomial expansion that might mathematically capture some departures of a real gas from the ideal gas law. This is in fact related to the *virial expansion* of the ideal gas law.