Homework / Assignments
Since Carter has many answers in the back of the book, you must show your work to receive credit for your answers.
Assignment #3
Carter
Video HW to be turned in separately--see Moodle for deadline
-
Carter, Chapter 3, problem 8
Notes / Answers
Carter Appendix A
Problem 3
In part b.) find $z(x,y)$ by integrating $dz$ along a 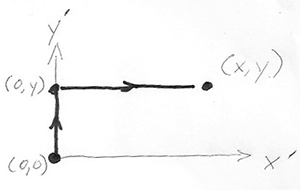 specific path from the the origin $(x',y')=(0,0)$ to a final point $(x',y')=(x,y)$ "in $x'$, $y'$ space". In particular, follow the path that runs from $(0,0)\to (0,y)$, and then $(0,y)\to (x,y)$.
specific path from the the origin $(x',y')=(0,0)$ to a final point $(x',y')=(x,y)$ "in $x'$, $y'$ space". In particular, follow the path that runs from $(0,0)\to (0,y)$, and then $(0,y)\to (x,y)$.
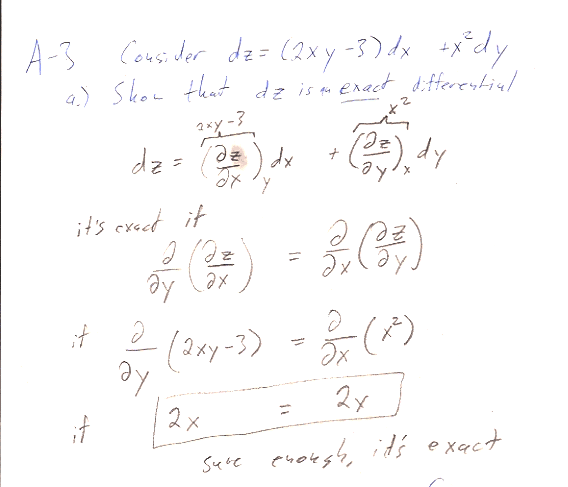
I asked you to find $z(x,y)$ by integrating along a particular path...

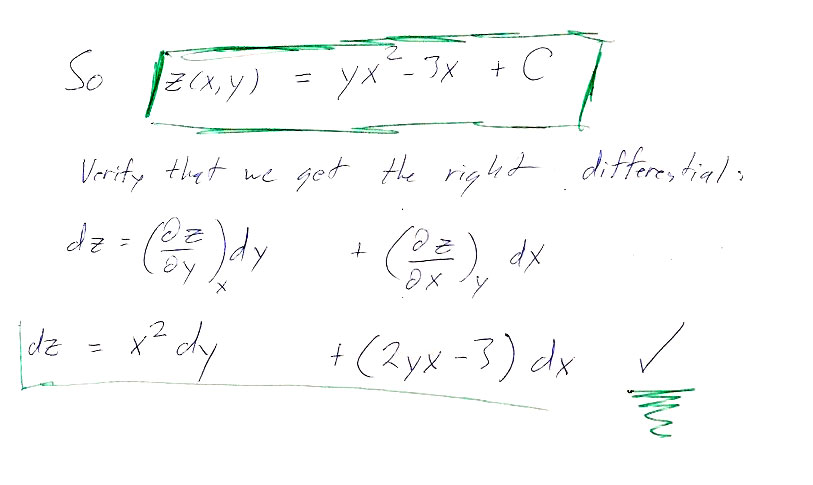
Here are the answers to the individual paths asked for in the problem:
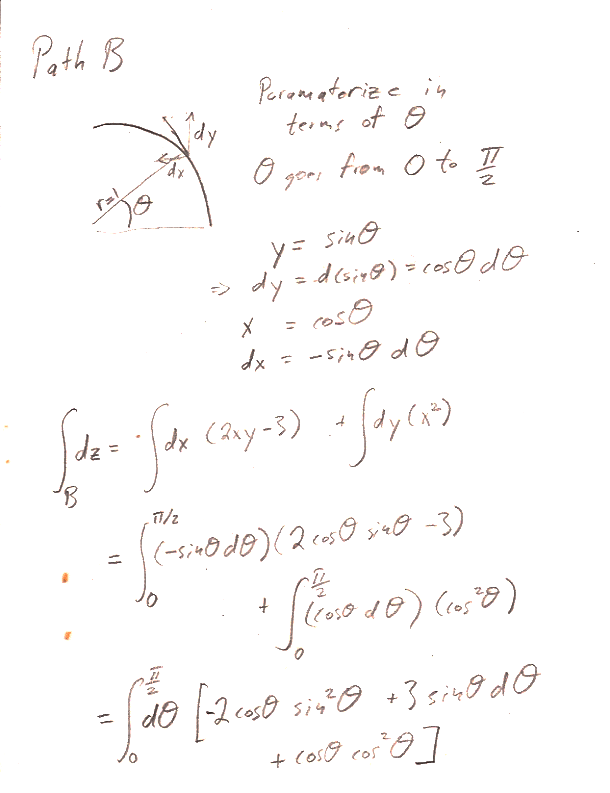

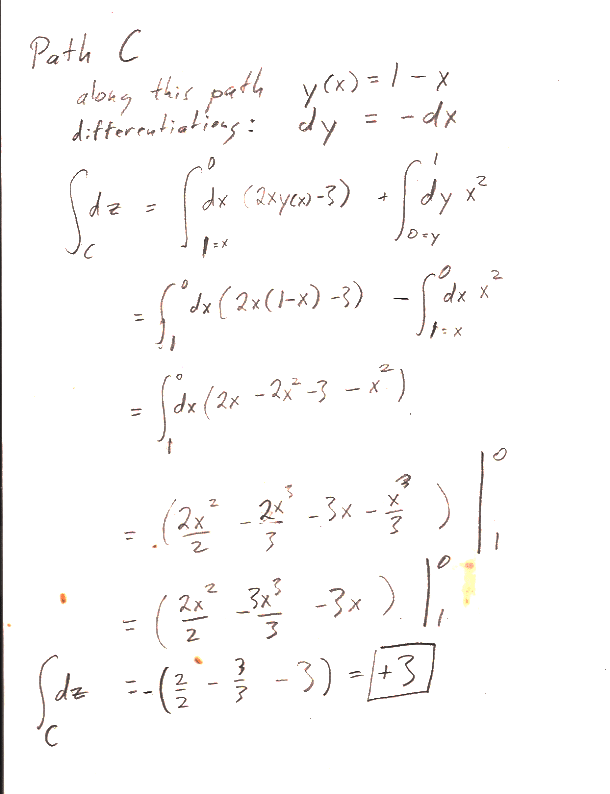
Carter Chapter 2
Problem 2-10
One approach is try out this trial equation of state and see if it gives the right $\beta$ and $\kappa$. Consider equations (2.13) and (2.14).
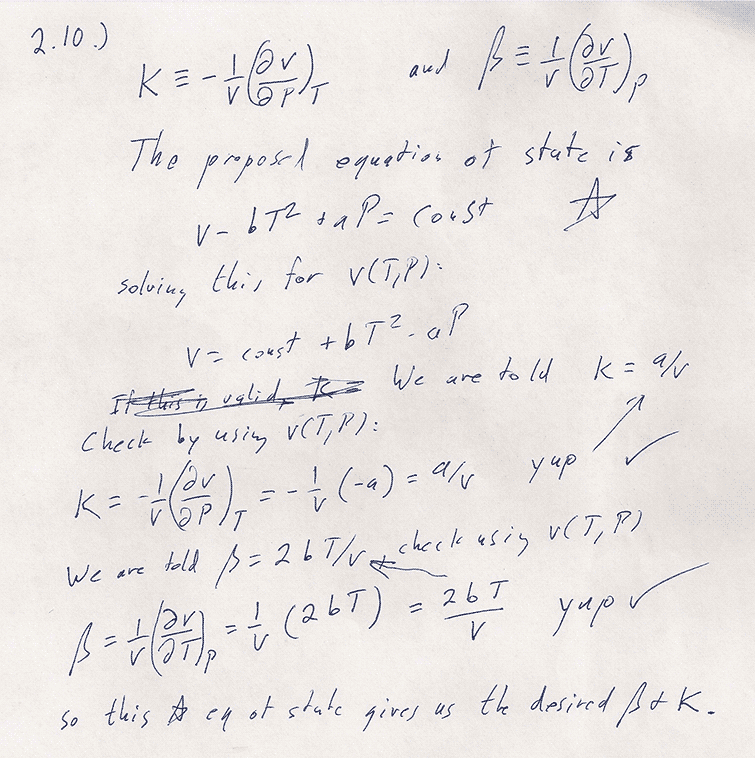
OR: integrate 2.17
Equation 2.17 is
$$dv=\beta v\,dT-\kappa v\,dP$$
Substituting $\beta=2bT/v$ and $\kappa=av$ into this...
$$\begineq dv=&(2bT/v)v\,dT-(a/v)v\,dP=2bT\,dT-a\,dP\\
\int dv=&2b\int T\,dT-a\int dP\\
\endeq
$$
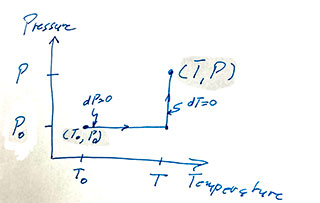 Since $v$ is a thermodynamic parameter, its differential is exact, and we can integrate along any path from some initial point to a final point, $v(T,P)$. Say along a path like this one...
Since $v$ is a thermodynamic parameter, its differential is exact, and we can integrate along any path from some initial point to a final point, $v(T,P)$. Say along a path like this one...
The upshot is $$\begineq v(T,P)-v(T_0,P_0)=&2b\left.\frac{T^2}2\right|^T_{T_0}-a\left.P\right|^P_{P_0}\\ v(T,P)=& bT^2-aP + (v(T_0,P_0)-T_0^2+aP_0)\\ v =& \color{blue}bT^2-aP + C \endeq $$
Carter Chapter 3
Problem 3-1
For an isothermal process, $T$ is constant. For an ideal gas, $P=\frac 1V nRT$ so, $$\begineq \Delta W &= \int_{V_i}^{V_f}P(V)\,dV\\ &=\int\frac{nRT}{V}\,dV\\ &=nRT\ln \left.V\right|_{V_i}^{V_f}\\ &=nRT\ln\left( \frac{V_f}{V_i}\right). \endeq $$ We are given the initial and final pressures (not the initial and final volumes). Solving the ideal gas equation for $V$: $V=\frac{nrT}{P}$. So, $\frac{V_f}{V_i}=\frac{P_i}{P_f}=\frac{1}{10}$, and the work done is: $$\begineq\Delta W &= nRT\ln(0.1)\\ &=10\text{ kMole }*8.314\times 10^3\text{ J/kmole}*300\text{ K }*(-2.30) &=-5.74\times 10^7\text{ J}\endeq$$
Problem 3-2
Work done is $\int P\,dV$. Since pressure is constant, $$\Delta W = P \Delta V=(30\text{ atm}\cdot 1.01\times 10^5\text{ Pa/atm}) (0.5(0.4/2)^2\pi)\text{[m^3]}=191\text{ kJ}.$$
Problem 3-3

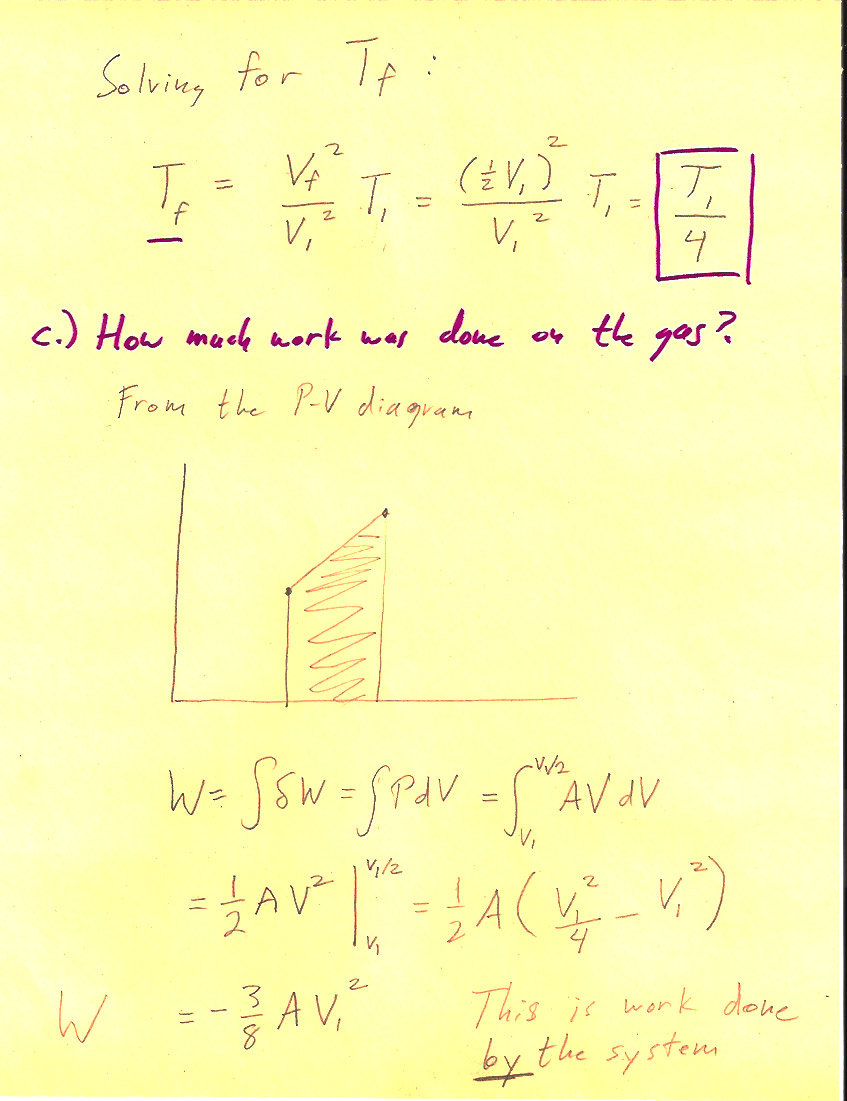

(1 pt) The work done *by* the system is $$\Delta W = \int P\,dV=-\frac{3}{8}nRT_i.$$ So, the work done *on* the system (by the surroundings) is $+\frac{3}{8}nRT_i$.
Problem 3-5
You might use CoCalc to do the integral and substitutions in problem 5. Here's a page showing How to substitute values into an expression in Sagemath. And here's one about assumptions: You may want to tell Sagemath to assume certain parameters are, for example, positive, before integrating. Here's a tip about using Assumptions to simplify definite integrals.

Since this is an isothermal process, $T$ is constant when integrating to find the work...

Carter Chapter 3
Problem 3-8
A gas in a frictionless piston. For the path $acb$ (below) 80 J of heat flow into the system, and the system does 30 J of work.
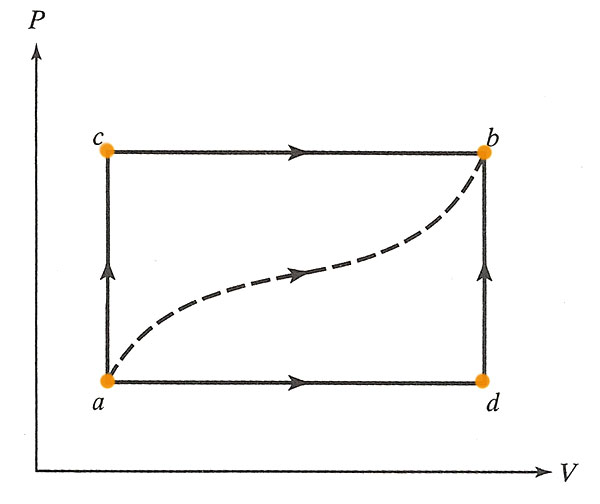
It's useful to write down the internal energy, $U$, at each vertex of the diagram for this problem. You may as well write down $U=0$ at point $a$: This is possible because adding a constant to the internal energy, $U+U_0$, will not change the first law, which only involves changes to the internal energy.
The internal energy, $U$ is a state variable, that depends only on (any) two thermodynamic variables--in this case we can use $P$ and $V$--and not on the path taken.
According to the First Law, a change in the internal energy...
$$\Delta U=\Delta Q - \Delta W$$
depends on the heat, $\Delta Q$, that flows in to the system, and the work, $\Delta W$, that the system does on its surroundings.
The initial information that we're given tells us that the difference in internal energy between $a$ and $b$ is:
$$\Delta U_{ab}=\Delta Q - \Delta U=80 J - 30 J = 50 J.$$
- How much heat flows into the system along $adb$ if the work done by the gas is 10J?
We still have $\Delta U_{ab}=50 J$, but for this process the work done is $\Delta W= 10 J$. The First Law says.. $$\begineq \Delta U_{ab} &= \Delta Q - \Delta W\\ 50 J &= \Delta Q - 10 J \endeq$$ So $\Delta Q = 60 J$$\equiv \Delta Q_{adb}$. - When the system is returned from $b$ to $a$ along the curved path the work done *on* the system is 20 J. How much heat is absorbed?
If $\Delta U_{ab}$ was 50 J, then for the reverse path, $\Delta U_{ba}=-50 J$. In this process, the work done *on* the system is +20 J, so the system does $\Delta W=-20 J$. The first law says... $$\begineq \Delta U_{ba} &= \Delta Q - \Delta W\\ -50 J &= \Delta Q - (-20 J)=\Delta Q + 20 J \endeq$$ So, $\Delta Q=-70 J$, which means that 70 J of heat flows *out* of the system.
- If $U_a=0 J$ and $U_d=40 J$, find the heat absorbed in the processes $ad$ and $db$.
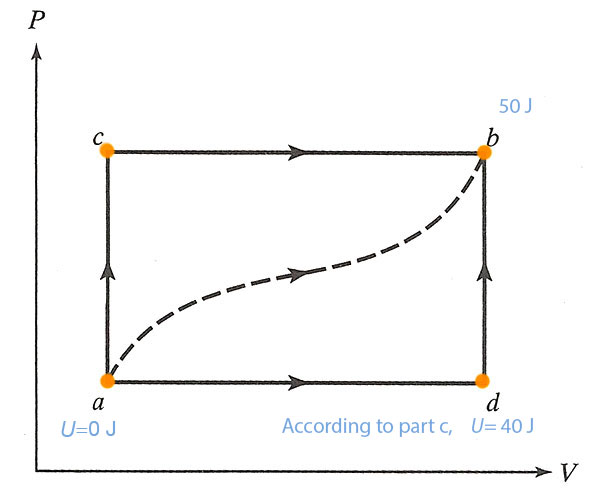
From (a) we know the total change in internal energy from $a$ to $b$: $\Delta U_{ab}=50 J=\Delta U_{ad}+\Delta U_{db}$. Here the new piece of information is that $\Delta U_{ad}=40J$. So, we can deduce that $\Delta U_{db}=10 J$.
For the process $db$, the First Law says: $$10 J=\Delta U_{db}=\Delta Q_{db} - \Delta W_{db}.$$ Since $V$ is constant along the path $db$, the work done on this path is zero, so $\Delta Q_{db}=10 J$.
For the process $ad$: From (a) we know the total heat for $adb$ was $\Delta Q_{adb}=60 J=\Delta Q_{ad}+\Delta Q_{db}$. We just calculated $\Delta Q_{db}=10 J$. So apparently, $\Delta Q_{ad}=50 J$.
Carter Chapter 4
Problem 4-1
For part c, calculate the mean heat capacity over that temperature range as (total heat)/(total temperature change). (You'll get a different answer from Carter--who apparently just averaged $c_V$ at the high and low temperatures.)

Correct units for answer are J/kmole/${}^o$K.
Assignment #4
Carter
Chapter 4: 2, 7, 8, 9a, 10, 12, 13
Notes / Answers
Carter Chapter 4
Problem 4-2
b.) One way involves using $c_P=\left(\frac{\del h}{\del T}\right)_P$ and calculating $h$ using (4.21).
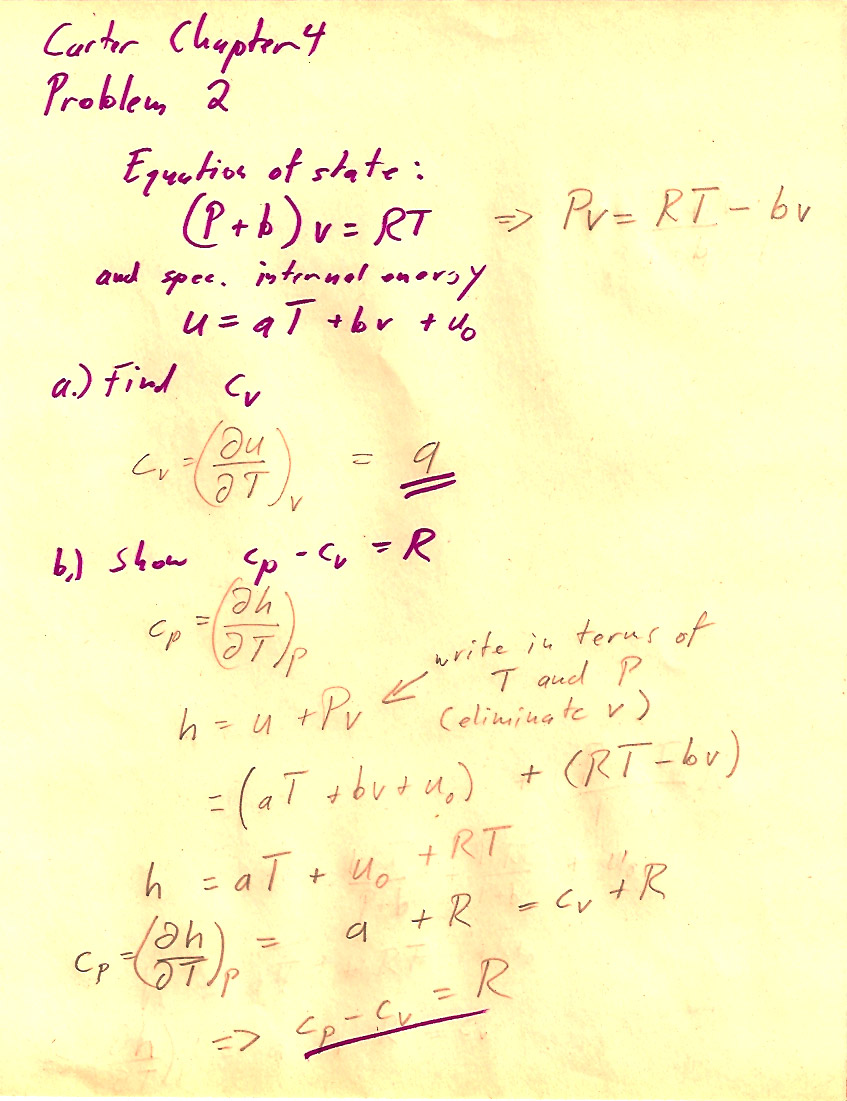
Carter Chapter 4
Problem 4-7

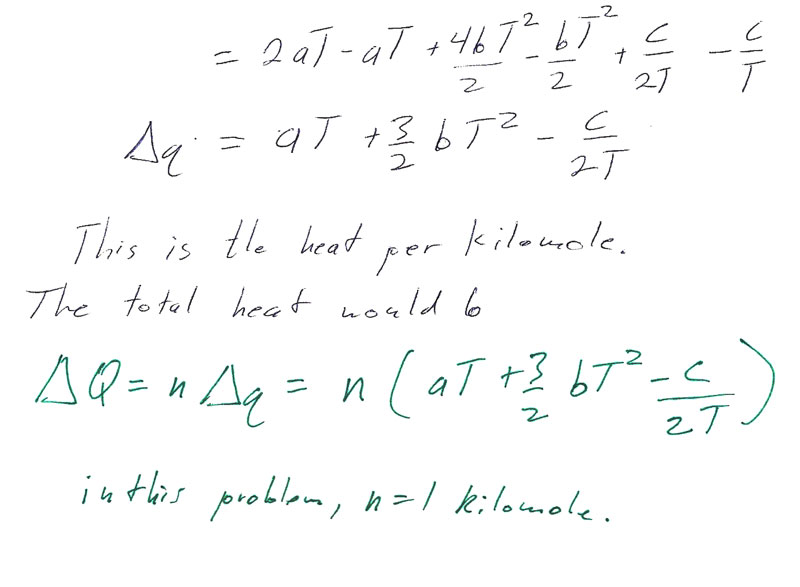
Carter, Chapter 4 - problems 8,9 are interrelated. 9a should be straightforward once you have 8a.
Problem 8b
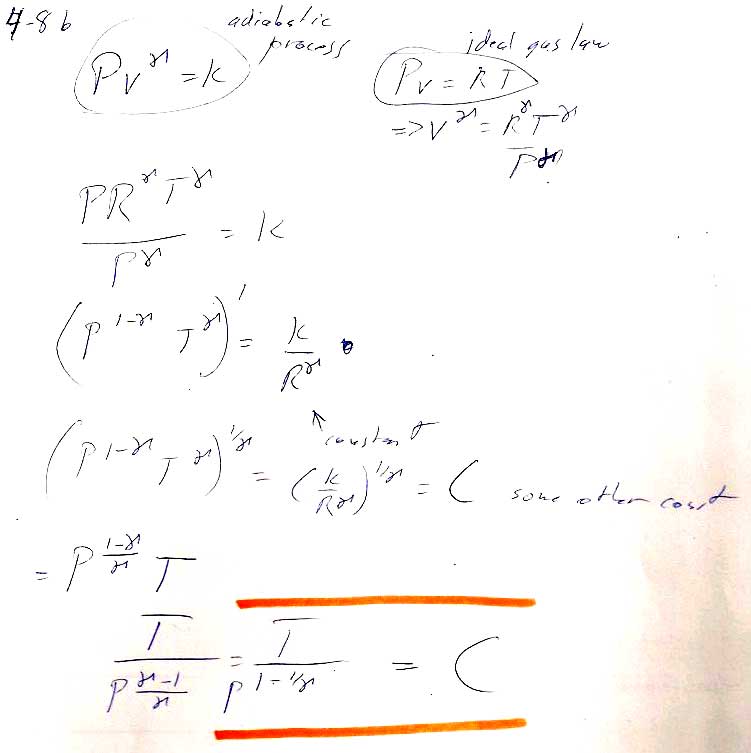
Carter, Chapter 4
Problem 4-10
a.) Show that for this system, an isothermal process is also isobaric. Show that for an isobaric process, $\Delta H=\Delta Q$. Now calculate the enthalpy, $H$.
b.) We're trying to get the relationship between $T$ and $V$. Gee, if we had some expression relating $dV$ to $dT$, which possibly involves functions of $V$, and $T$ as well, we could perhaps use the separation of variables technique to group similar terms and integrate.
Inspired by this thought, consider that we can think of a state function, like $U$, as a function of any two thermodynamic parameters we like. So, think of $U(T,V)$ as a function of $T$ and $V$. Then, the differential of $U$ (the Pfaffian) is: $$dU=\left(\frac{\del U}{\del T}\right)_V dT +\left(\frac{\del U}{\del V}\right)_T dV$$ [Do you have any way of calculating those partial derivatives?]
And, we are supposed to consider an adiabatic process, such that $\delta Q=0$. That might remind you of the first law: $$dU=\delta Q -\delta W=\delta Q- PdV$$ [How can you get $P(T,V)$? Put in your assumption that $\delta Q$=0...]
Now you have two different expressions for $dU$, so you can set them equal to each other...

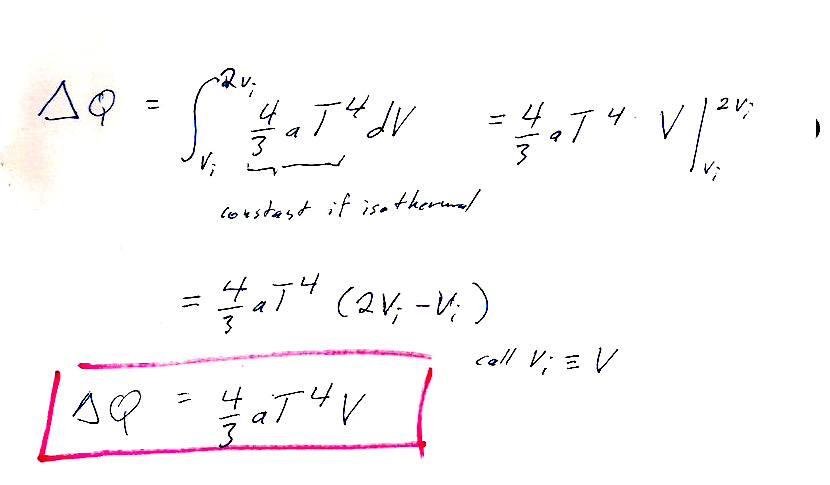
Luke had a more straightforward approach: Using the expressions given for $U$ and $P$, you can directly calculate the enthalpy:
$$H=U+PV=aT^4V+\left(\frac{aT^4}{3}\right)V=\frac 43 aT^4V.$$
Now we consider an initial state with $V_i=V$ and $V_f=2V$, and $T$ is constant. So, we can easily calculate $$\Delta H=H_f-H_i=2*\frac 43 aT^4V-1*\frac 43 aT^4V=\frac 43 aT^4V.$$
That looks like our answer! But wait... It's $\Delta H$, not $\Delta Q$ :-<. What's the connection with heat flow?
From Table 4.2, we have:
$$dh=\delta q+v\,dP$$. So $dh=\delta q$ only if the process is isobaric, and we have an isothermal process.
But look at the pressure given to us: $P=aT^4/3$. This means if the temperature is constant, there will be no change in the pressure. So for this system, an isothermal process is also isobaric! And for an isobaric process $\Delta H=\Delta Q$.
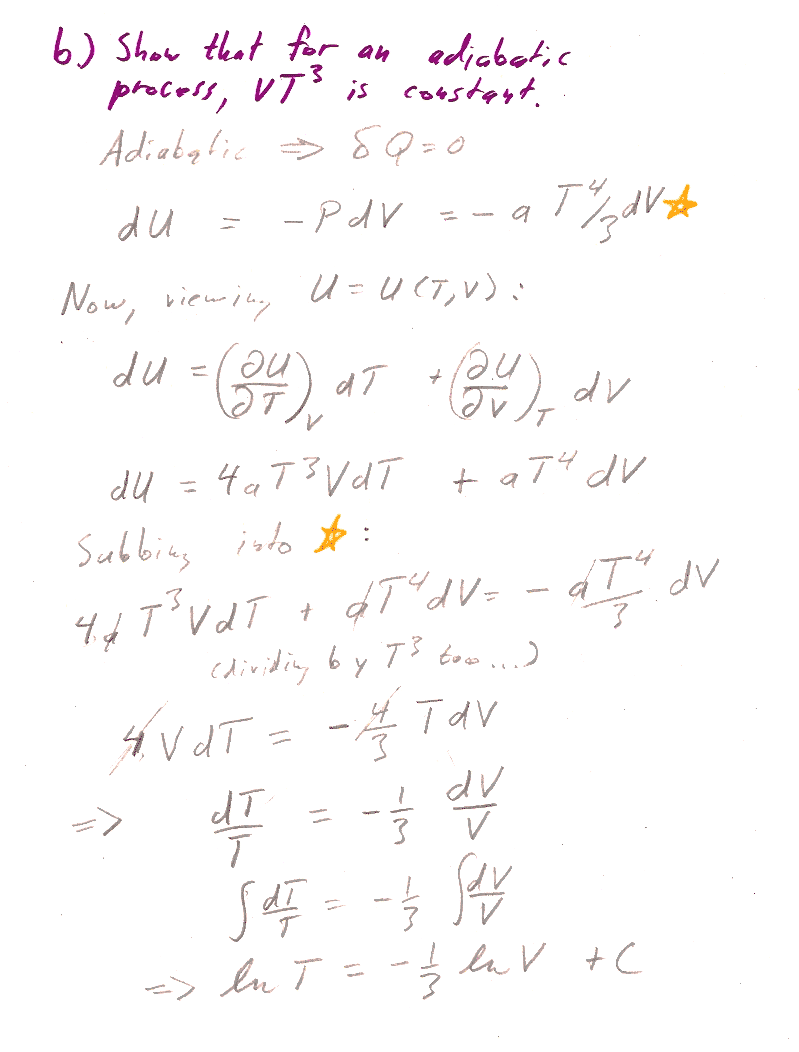

Carter, Chapter 4
Problem 4-12 --
b)There are two *different* approaches you can take. In outline form:
1.) [Deeksha's approach] Start from the definition of $H=U+PV$.
- The differential of enthalpy is $dH=dU+PdV+VdP$.
- Using the fact that the process is adiabatic, together with the first law, make the argument that for an adiabatic process this simplifies to $dH=VdP$
- Using our expression $PV^{\gamma}=K$, you can solve for $V(P)$, and integrate $dH$ from initial to final pressure (See 4.12a) to find the change in enthalpy.
- Some simplification will be required to get the book's answer.
2.) A second approach involves integrating $C_P$:
- We said that, for an ideal gas, both internal energy, $U$, and enthalpy, $H$, are functions of $T$ alone (no dependence on $P$) and therefore $c_P=\frac{dh}{dT}$ or $C_P=\frac{dH}{dT}$ (not a partial derivative, but just a derivative with respective to one variable).
- So, you can find the change in enthalpy by integrating $C_P$ (It's a constant--found from Mayer's law...) from initial to final temperature.
- You can use the ideal gas law and the results of part 4.12a to find the initial and final temperature.

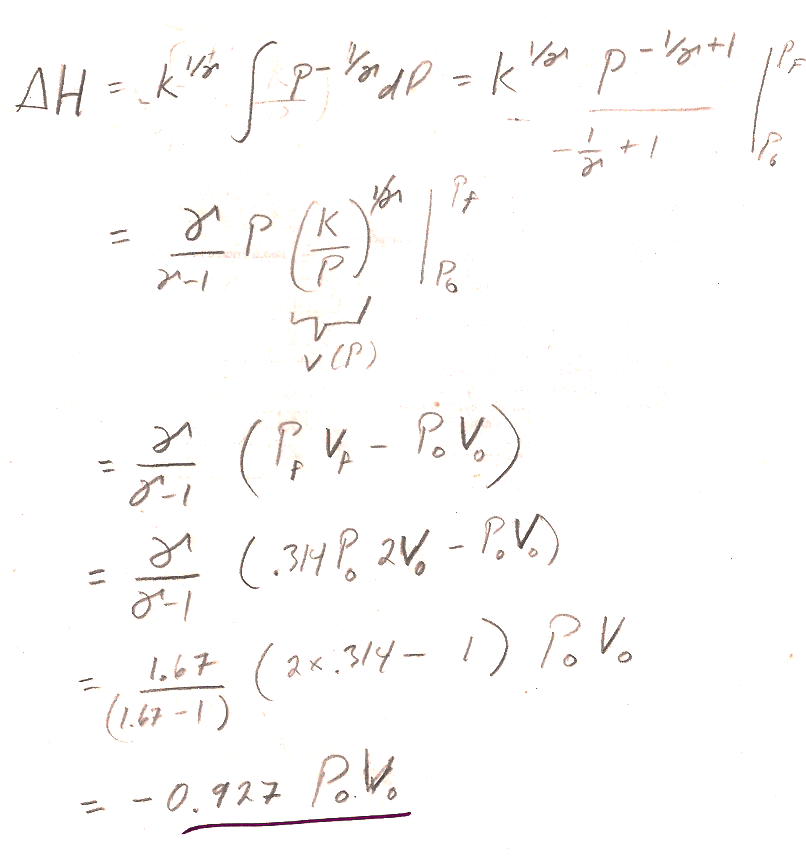
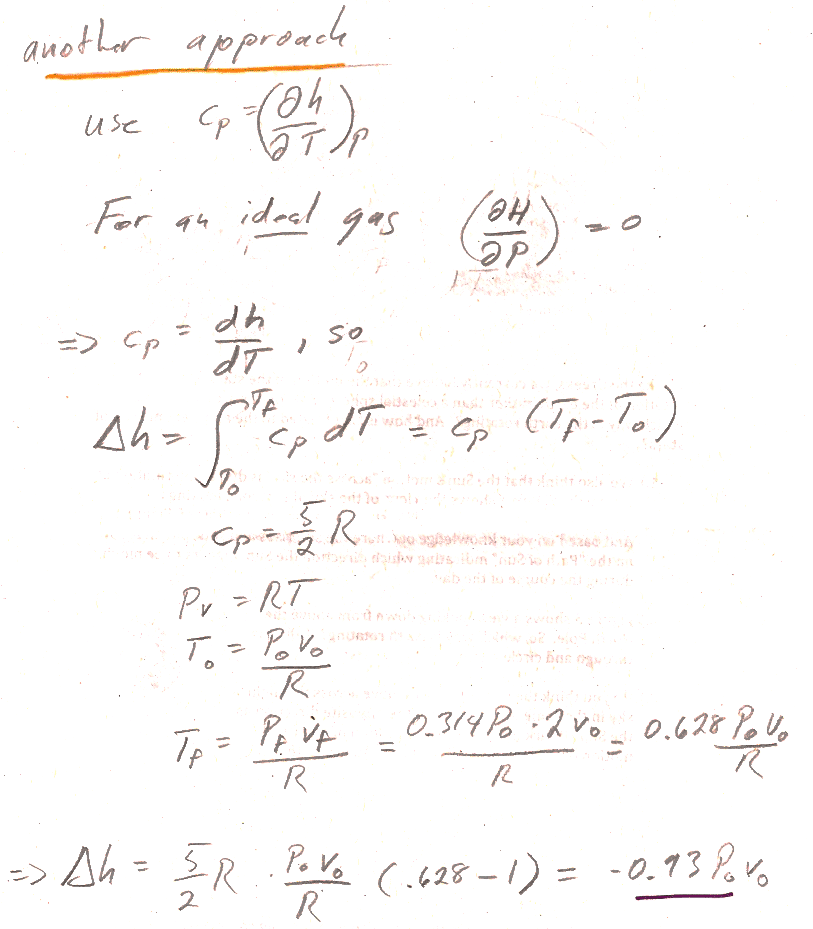
Carter, Chapter 4
Problem 4-13
A striking result is that the latent energy of vaporization (538 kCal/kg) is more than half of the total enthalpy change.

You'll need to look up the latent heats for each phase transition.
-1 pt if the latent heats mysteriously appear in your problem writeup without being labelled or explained.

Carter, Chapter 4
Problem 4-14
Use these writing conventions to keep your thinking clear...
- specific (per kilomole) quantitites in lower case,
- total (not per kilomole) quantities in upper case.
I suggest that you do something similar to keep your thinking clear on the difference. For example:
- $\Delta U=U_f-U_i$ is the total change in internal energy,
- We're given the specific heat capacity, $c_v=5R/2$, so $C_v=nc_v$
$P_i= 270$ kPa; $P_f=300$ kPa; $V=V_i=V_f=0.057$ m${}^3$.
Since it's an ideal gas, $U=U(T)$ and $$\Delta U=\int dU=\int_{T_i}^{T_f}C_v\,dT=nc_v(T_f-T_i)=\frac 52nR(T_f-T_i).$$ Using the ideal gas law, $nRT=PV$, so... $$\begineq\Delta U&=\frac 52V(P_f-P_i)=\frac 52(0.057\text{m}^3)(300-270\text{kPa})\\ &= 4.28 kJ \endeq $$