Homework / Assignments

Assignments: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Assignment #8

PMR 1: The derivation of the Claus.-Clap. equation assumes that volume/kilomole $v_g \gg v_l$. Calculate for water, at 100 C and 1 atm, the ratio $v_g/v_l$. Use the ideal gas law for the vapor phase, and use the density of water in the liquid state ~ 1 g/cc.
PMR 2: Estimate the temperature at which water boils when the atmospheric pressure is 3 atm. The latent heat of water is $l$=40 kJ/mole (at 100 C).

Carter
 Chapter 8: 13, 14
Chapter 9: 1, 2

Answers: [Show]   [Hide]

Notes / Answers

PMR 1

$$\frac{v_g}{v_l}=1.7\times 10^3$$

PMR 2

Using the integrated form (Carter, eq 8.33) of the Clausius-Clapeyron equation, the boiling point at 3 atm is 407 K=135 C.

Carter Chapter 8
Problem 4cd

(c) Derive: $H=G-T(\del G/\del T)_P$.

$$G=U+PV-TS = H-TS$$ Rearranging to get $H=G+TS$ and using the Maxwell relation that $S=-(\del G/\del T)_P$ gives us the desired relationship.

(d) Derive: $C_P=-T(\del^2 G/\del T^2)_P$. (reversible process)

You could take advantage of your answer in (c), or you could start with one of the $T\,dS$ equations...

The 'reversible process' comes in this way: In general, if we heat an object, the ratio of small quantity of heat needed to change an object by small temperature (at constant pressure) is $(\delta Q/\del T)_P$.

If the process is reversible, then this ratio is $(\delta Q_r/\del T)_P =(\del H/\del T)_P = C_P$.

Two ways to do this problem...

  1. $C_P=(\del H/\del T)_P$ Take the expression from (c) and take the partial derivative wrt $P$: $$\begineq\left[\frac{\del H}{\del T}\right]_P &= \left[\frac{\del}{\del T}\{ G-T\left(\frac{\del G}{\del T}\right)_P\}\right]_P\\ C_P &=\left(\frac{\del G}{\del T}\right)_P - 1*\left(\frac{\del G}{\del T}\right)_P -T\left(\frac{\del^2 G}{\del T^2}\right)_P\endeq$$
  2. The other way was to start with the $T\,ds$ equation (7.11): $$Tds=c_PdT-T\left(\frac{\del v}{\del T}\right)_PdP.$$ for a constant pressure process, $dP=0$, and we can write (in terms of extensive variables) $[TdS]_P=C_PdT$, which you can re-arrange as $C_P=T\left(\del S/\del T\right)_P$.

    Then, you write $S=-\left( \del G/\del T \right)_P$, and you're within a step of the desired result.

Carter Chapter 8
Problem 13

a.) The sublimation curve and the vaporization curve (and the fusion curve too) all meet at the triple point. So, if we set $\ln P_\text{sub}=\ln P_\text{vap}$ we can solve for the temperature: $$0.04-6/T = 0.03-4/T$$ $\Rightarrow T=200$ K.

b.) For both liq$\to$vap and solid$\to$vap, the volume/kmol of the vapor is much greater than the the other phase. This is one of the approximations used in my notes that allows you to use separation of variables on the Clausius-Clapeyron equation, and then integrate...

so we can write both equation (8.30) and (8.31) (the equations for the liq/vap and the solid/vap coexistence curves) as: $$\frac{dP}{dT}\approx\frac{\ell}{Tv_\text{vap}}=\frac{\ell}{T(RT/P)}$$ where I've used the ideal gas law to write $v_\text{vap}=RT/P$. Separating the variables leads to: $$\begineq \frac{dP}{P}&=\frac \ell R \frac{dT}{T^2}\\ \int\frac{dP}{P}&=\frac \ell R \int\frac{dT}{T^2}\\ \ln P&=-\frac{\ell}{RT}+C \endeq $$ Comparing this to the equations given...we find $\ell_\text{sub}=6R$ and $\ell_\text{vap}=4R$

c.) See Fig 4.2 and Eq. (4.18). We have: $$\ell_\text{sub}=\ell_\text{fus}+\ell_\text{vap}$$ Solving for $\ell_\text{fus}=6R-4R=2R$.

Carter Chapter 8
Problem 14

The motivation for this problem: The low friction of an ice skater is due to a layer of water on top of the ice. In some intro physics courses, it is claimed that, at temperatures below freezing, the weight of an ice skater is what melts the ice.

The author of this Journal of Physics article uses the results of what you'll calculate, together with an estimate of the surface area of an ice-skating blade in contact with the ice of about $10^{-4}$ m^2 to cast doubt on this explanation.

a.) See the development leading up to the second equation below (8.33) (p. 141 in Carter): $$\Delta T = \frac{T(v_\text{liq}-v_\text{sol})}{\ell_\text{fus}}\Delta P.$$ The slope of the fusion curve (in Pa/K) is: $$\frac{\Delta P}{\Delta T}=\frac{\ell_\text{fus}}{T\Delta v}=\frac{3.34\times 10^5\text{J/kg}}{273.15\text{ K }\cdot-9.05\times 10^{-5}\text{ m^3/kg}}=1.35\times10^{7}\text{ Pa/K}.$$ [Units are (J/m^3)/K=(Nm/m^3)/K=(N/m^2)/K=Pa/K.]

Assuming the slope is not changing very much, and it runs through the point $(P,T)=(1.01\times 10^5\text{ Pa}, 273.15\text{ K})$... $$\frac{\Delta P}{\Delta T}=\frac{\Delta P}{-2 K}=-1.34\times10^7.$$ Solving, we find $\Delta P= 2*(1.34\times10^7)$ Pa. So the pressure at which it starts to melt is: $$(1.01 \times 10^5+2.68\times 10^7) \text{ Pa}\frac{1\text{ atm}}{1.01\times 10^5 \text{ Pa}}\approx 269\text{ atm}.$$

Back to the ice-skating problem...A quick calculation for a 100 kg person (=1000 N) putting their weight on two ice-scating blades at, let's say momentarily 2*5mm*10mm=$100\times 10^{-6}$ m^2. The pressure is 1000 / 0.0001=10^7 Pa~100 atm on the ice. Seemingly not enough to melt the ice! And ice-skating is possible down to much lower temperatures (~20 C).

The solution is a surface effect, sometimes called premelting: The water molecules close to the surface of the ice are not bound to as many nearest neighbors as the molecules in the bulk. And so, even below the (bulk) melting temperature, 0 C, of water, there a few molecular layers of water on the surface already without any additional pressure. (Dosch H, Lied A, Bilgram J. Glancing-angle X-ray scattering studies of the premelting of ice surfaces. Surf Sci. 1995;327(1-2):145–164.)

Carter Chapter 9
Problem 1



Carter Chapter 9
Problem 2

In both parts a) and b), we're working with a fixed amount ($dn=0$) of ideal gas. But you can *still* get an expression for the chemical potential, by using $\mu=g=G/n$.

Part a) You could start with the $Tds$ equation in terms of $T$ and $V$ to get an expression for $ds$ that you could integrate to get the expression for $S$. Assume for the time being that $c_V$ and $c_P$ are constants. Remember that the the enthalpy of an ideal gas is a function only of the temperature.

Part b) You could start from the $Tds$ equation in terms of $T$ and $P$. But there is an even shorter route to the answer by starting with the expression for $dG$ in table 8-1. (We're interested in a constant $T$ process...)

Two typical issues with this problem:

  • Account for $n$ properly. Distinguish carefully with upper and lower case: $c_V=C_v/n$ and $c_P=C_P/n$ $V,S,G$ and $v,s,g$. Then, $G/n = g = \mu$.

  • Justify how you get $H=C_PT+H_0$ (This is not a universal thermodynamic identity): Typically, any exact thermodynamic variable is a function of two parameters, e.g. $H=H(T,P)$, or $H=H(T,V)$. It is only because we know that we're dealing with an ideal gas that we know $H=H(T)$ is only a function of $T$, and thus the Pfaffian of $H$ is $dH= \frac{dH}{dT}dT=C_PdT$ instead of something harder to integrate like $dH=\frac{\del H}{\del T}dT + \frac{\del H}{\del V}dV$.



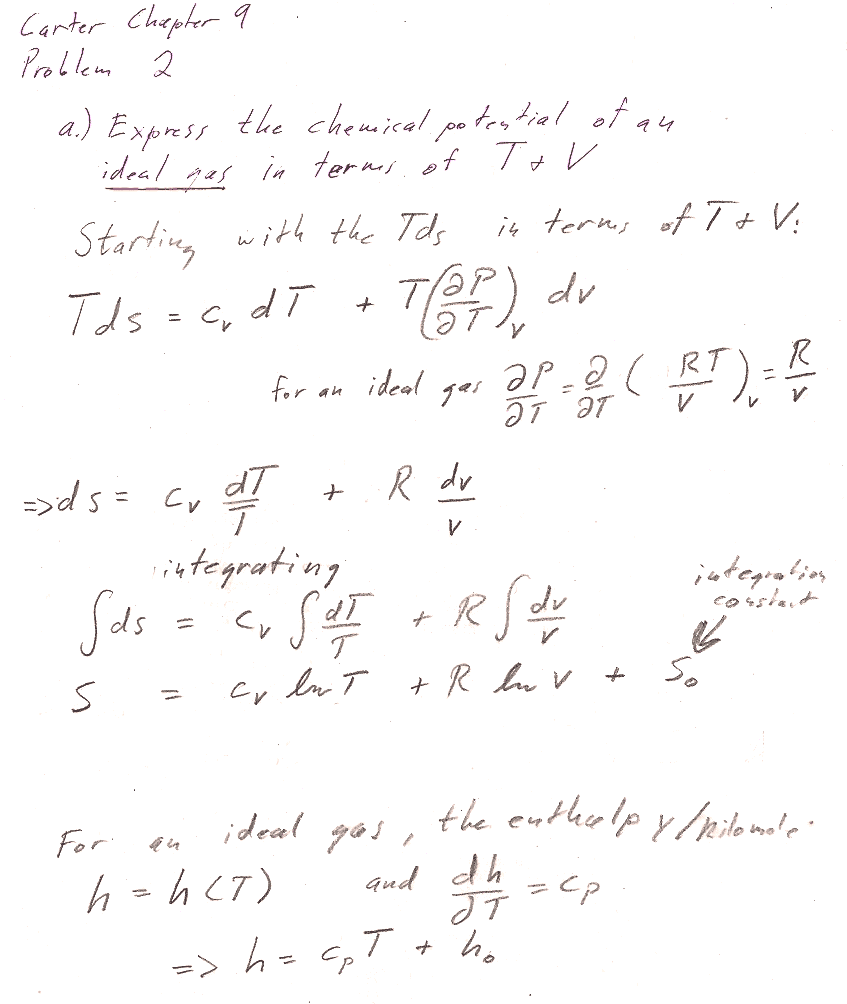
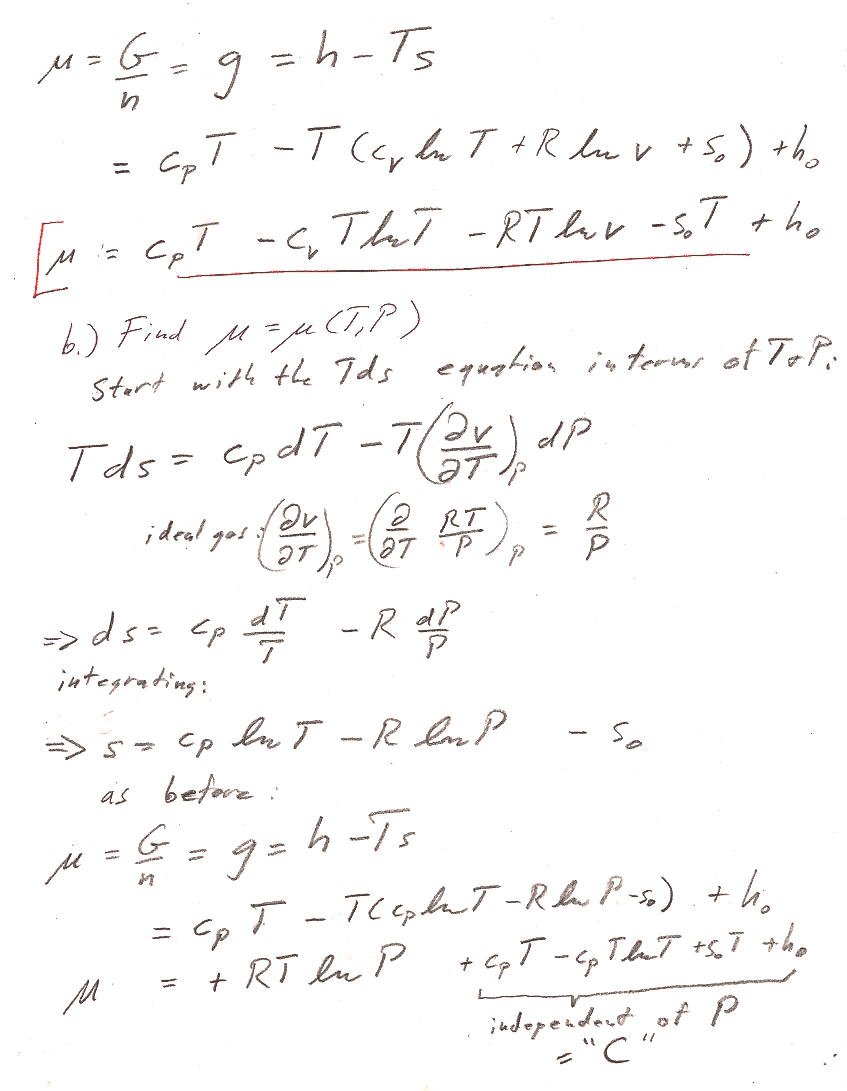
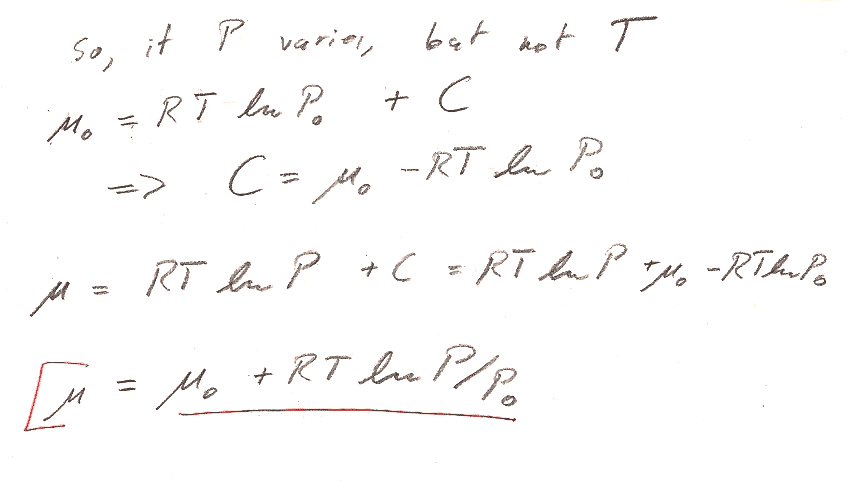
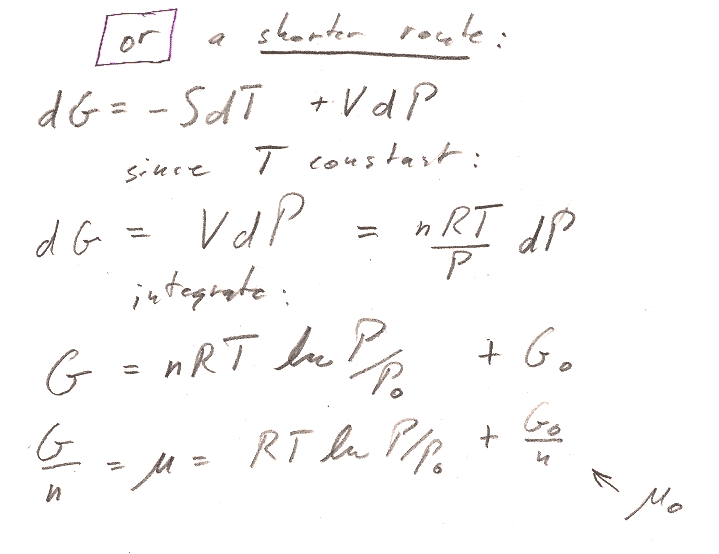
Assignment #9

Carter
 Chapter 9: 3, 5 (with PMR variations), 6, 8, 9
Chapter 11: 1 , PMR: 11.7 graphs of $N_{MB}(v)$ with $N=1000$.

Answers: [Show]   [Hide]

Notes / hints / answers

Carter Chapter 9
Problem 3
In section 9.5 we looked at entropy of mixing...




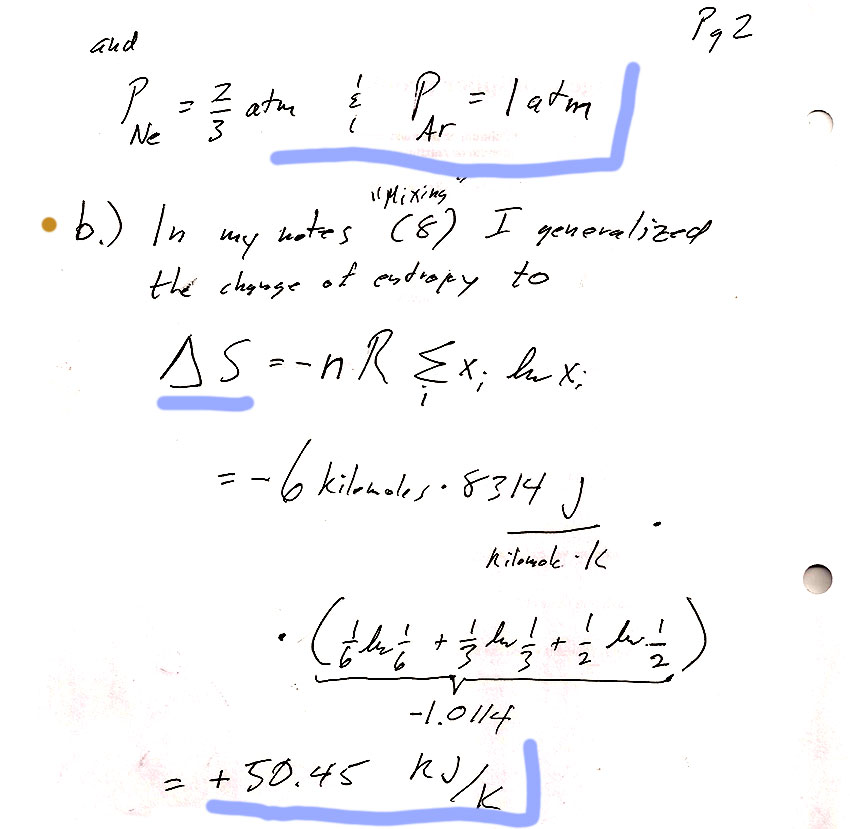
Carter Chapter 9
Problem 5- PMR version

  1. A mixture of gold and thallium can exist in equilibrium with four phases present. The four phases are liquid solution (or "melt"--a liquid containing both Au and Tl.), vapor, solid gold, and solid thallium.

    [Re-read Carter's definition of phases on page 157: There are two different solid "phases", because solid gold will not interdiffuse with the solid thallium. However, only one liquid "phase" exists because gold and thallium do interdiffuse in the liquid phase. If we were talking about liquid oil and liquid water, we could designate those as two different liquid phases, because oil and water do not interdiffuse.]

    How many different components, $k$? How many different phases, $\pi$? And therefore, what is the variance when all of these components/phases are in equilibrium with each other? (This is called the "eutectic point".)

    The number of degrees of freedom, or variance, $f$, is $$f=2+k-\pi$$ There are two components (Gold and Thallium). How many "phases"?
    1. Solid Tl
    2. Solid Au (see note above, these count as two separate "phases".)
    3. Tl-Au melt

    If it were only these three phases, the variance would be 2+2-3=1. But the Eutectic point is uniquely determined, and should have 0 variance. So we need one more phase. The fourth phase is the Tl-Au vapor. With this, the variance will be 0.

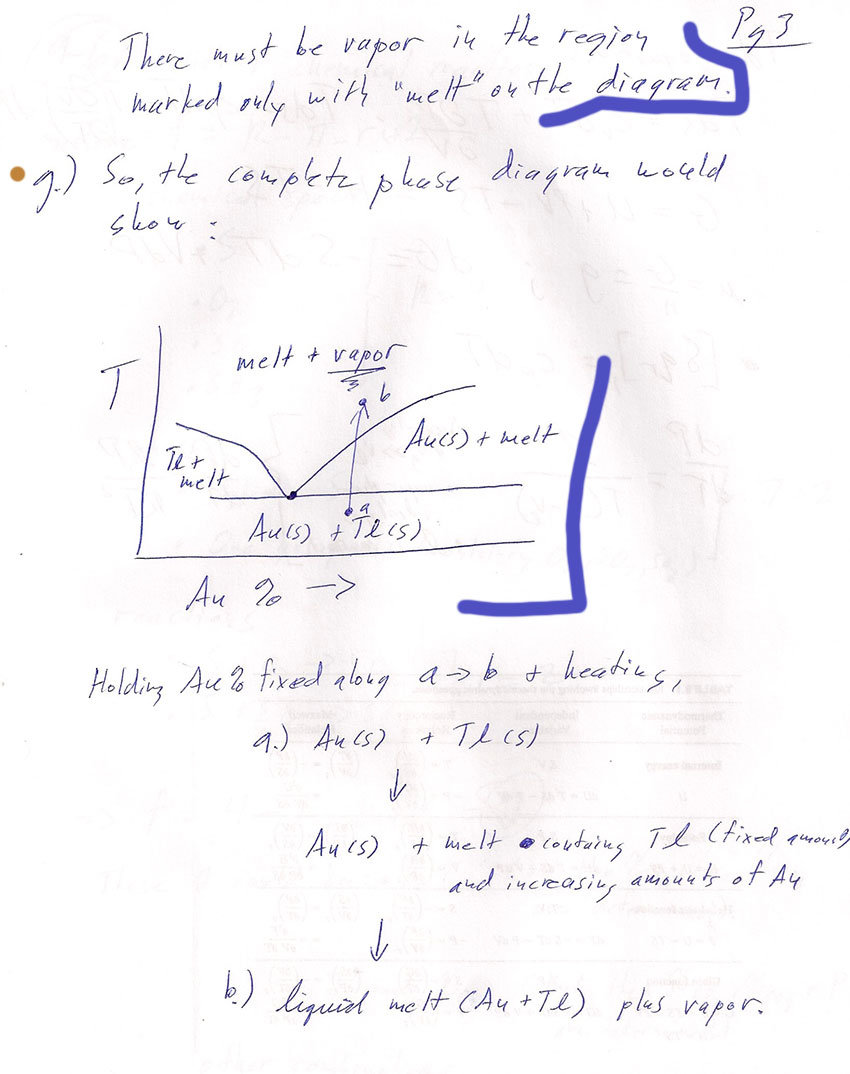
  2. The phase diagram of gold and thallium is shown below. (from Bala Ramachandran, Louisiana Tech University). Mark on there, or give the coordinates of the eutectic point.

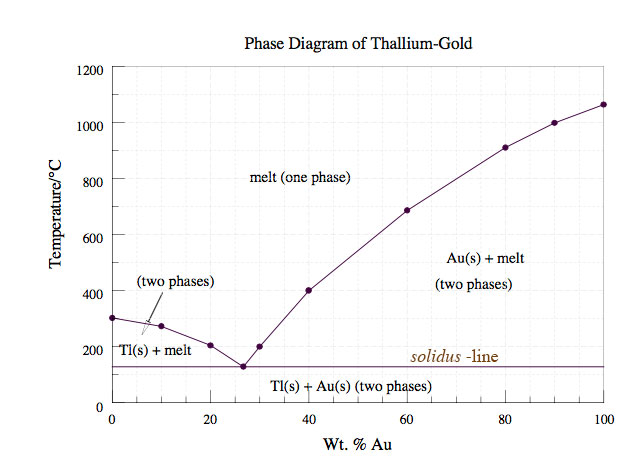
    It's the point on the solidus where the other co-existence curves meet.

  3. The phase diagram above shows no indication of vapor. It only shows the non-vapor phases. So, let's work out in which regions there is vapor (and where there is none):

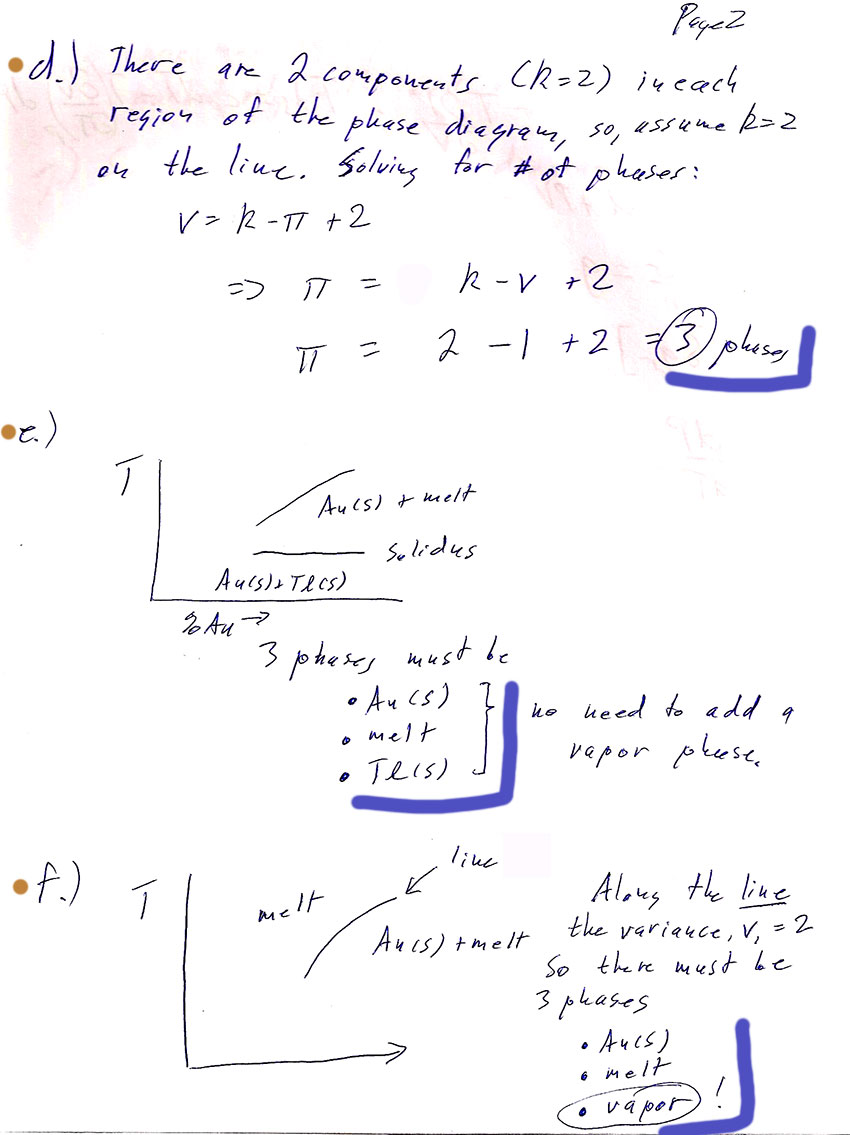
    What is the variance of a line on a phase diagram? (Such as the solidus, or the boundary of the single-phase melt region.)

    The variance of a line is $f=1$.

  4. How many phases must be in equilibrium along any of the lines on the phase diagram above?

    Certainly we have two components, $Tl$ and $Au$, everywhere in the diagram. So $k=2$. Therefore: $$f=1=2+k-\pi=4-\pi.$$ So we must have $\pi=3$ phases in coexistence along any of the coexistence lines.

  5. How many, and which phases are in equilibrium along the right-hand section of the solidus line--that is, when the Gold percentage is greater than about 30%? (Add in a vapor phase if you need it to make the number of phases come out right for the variance of a line.)

    Along that line we have $Au(s)$, $Tl(s)$, and melt in coexistence. This is already 3, so we don't need vapor on either side of the line.

  6. How many, and which phases are in equilibrium along the right-hand, rising line that forms the boundary of the "melt (one phase)" region? (Add in a vapor phase if you need it to make the number of phases come out right for the variance of a line.)

    We only see $Au(s)$ and melt on either side of the line. That's only two phases. We need the vapor phase. It should be on the "melt" (only) side of the line, because if there were vapor on the $Au(s)$+melt side, the solidus-line would be overdetermined.

  7. What do you conclude about the regions of the phase diagram in which the vapor phase exists? Consistency check: Do you have vapor in at least one of the regions in contact at the eutectic point?

    The top region marked "melt (one phase)" must also have vapor phase present. That's the only area of the phase diagram with vapor. And now, at the eutectic point we'll have the required 4 phases in coexistence.




Carter Chapter 9
Problem 6


Carter Chapter 9
Problem 8

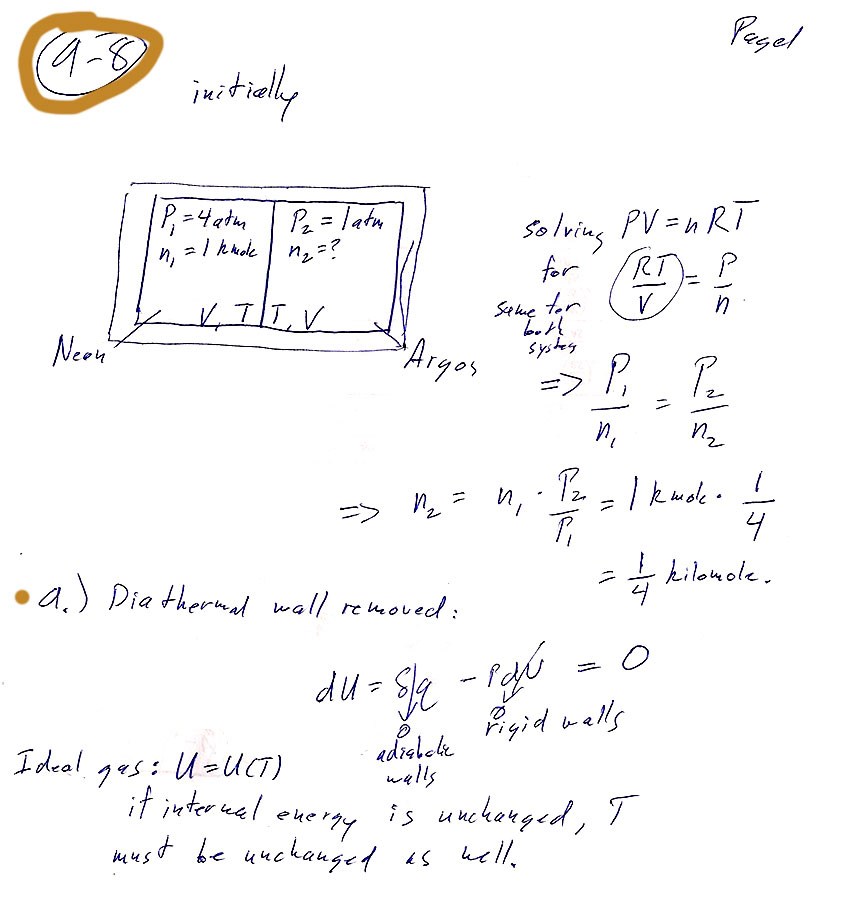
a) Explain how you came up with the final temperature of the system.




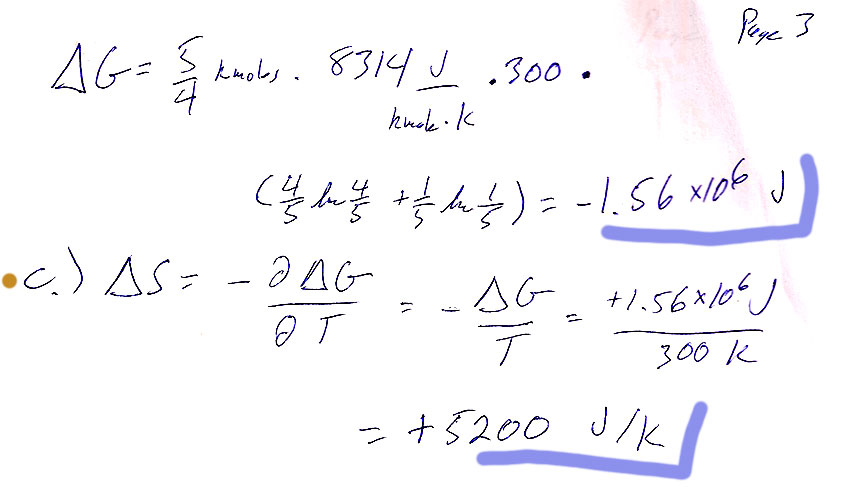
Carter Chapter 9
Problem 9

b.) The approach is to solve the van der Waals equation of state for $P$, find $[dP/dV]_{T,n}$, use separation of variables to get $dP=(\text{lotsa stuff})dV$ , and finally multiply by $V$, because you can integrate: $\int V\,dP=\int dG$ to get $G$.

When I integrated $\int P\,dV$ I got an answer that differed from Carter's by one factor of $T$: $$G=-nRT\ln(V-nb)+\frac{n^2bR\color{red}{T}}{V-nb} -\frac{2n^2a}{V}+C(T)$$



Carter Chapter 11
Problem 1

You can carry out any integrals you need to do in CoCalc or WolframAlpha or Mathematica.

In section (d) the notation, may be a bit obscure: You should show that $$\sigma=\left[\bar{\,v^2\,}-(\bar v)^2\right]^{1/2}$$ "The square root of [ the average value of ($v^2$) minus (the average value of $v$)${}^2$]."

Hint: You'll need to write out the mean quantities in terms of integrals. See Carter's equations 11.2-11.4. Then you can group and re-group quantities in the integral to prove relationships, without ever needing to evaluate any integrals. For example, this is how you could prove that $\overline{a(v)+b(v)}=\overline{a(v)}+\overline{b(v)}$: $$\begineq \overline{a(v)+b(v)}&=\int_0^\infty (a(v)+b(v))\,f(v)\,dv\\ &=\int_0^\infty a(v)\,f(v)\,dv +\int_0^\infty b(v)\,f(v)\,dv\\ &=\overline{a(v)} +\overline{b(v)}\\ \endeq$$





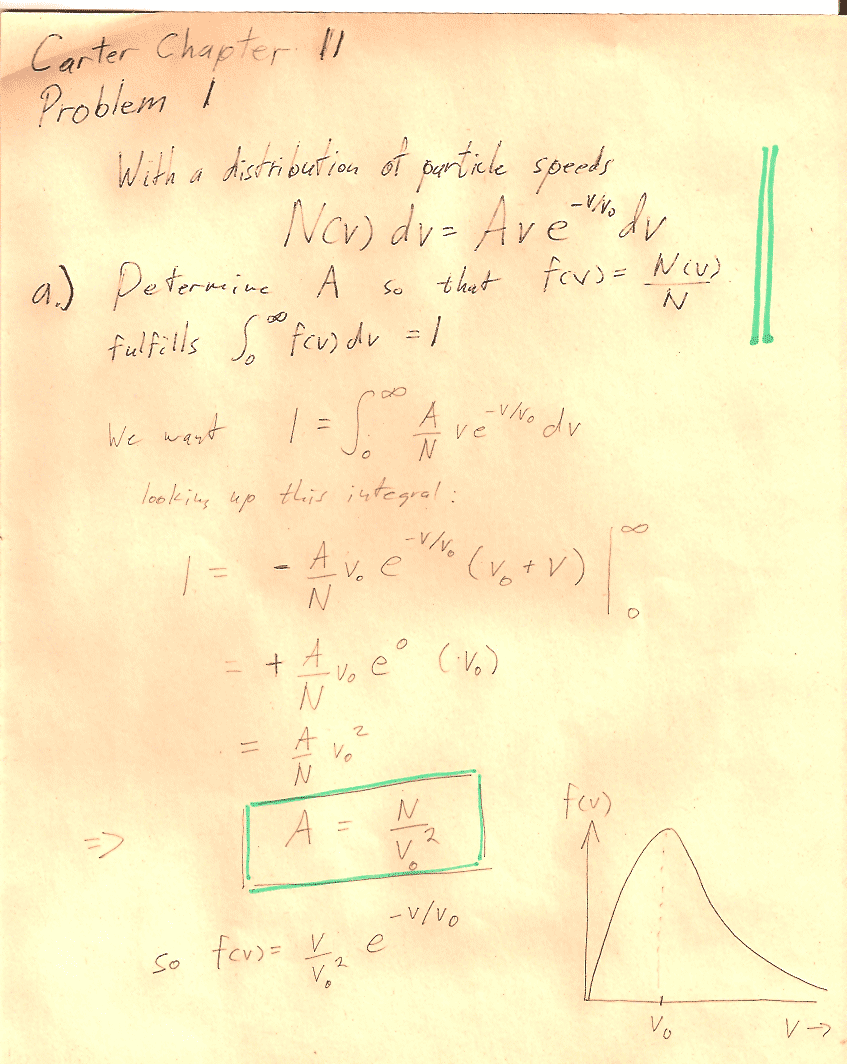
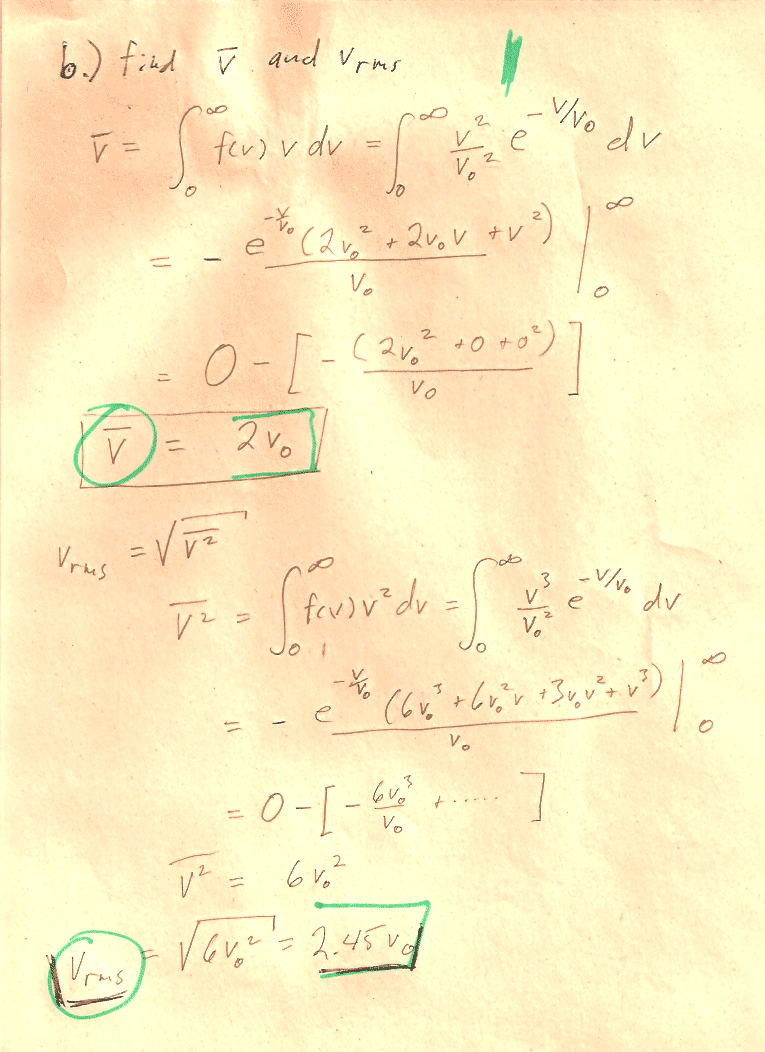
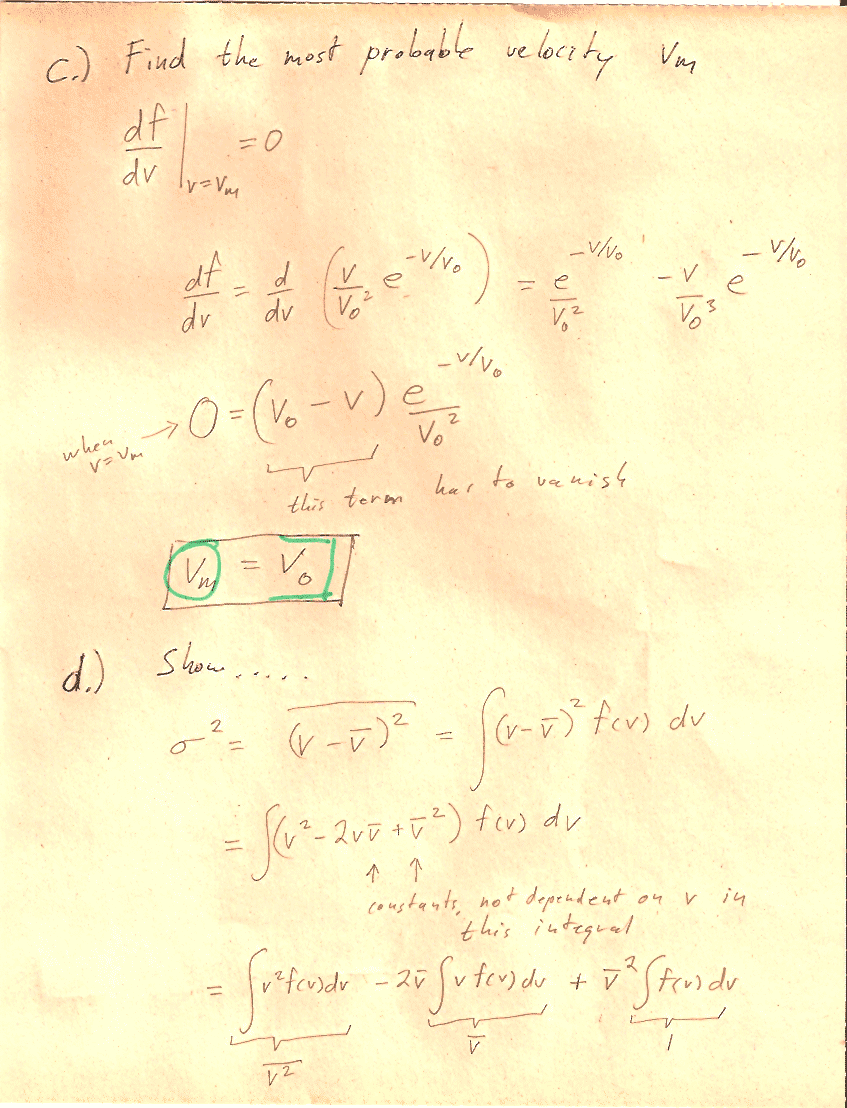
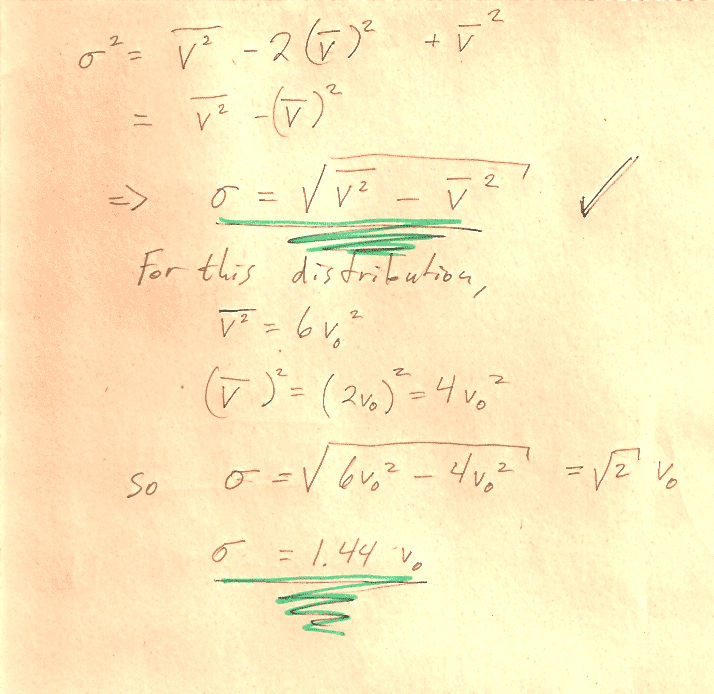
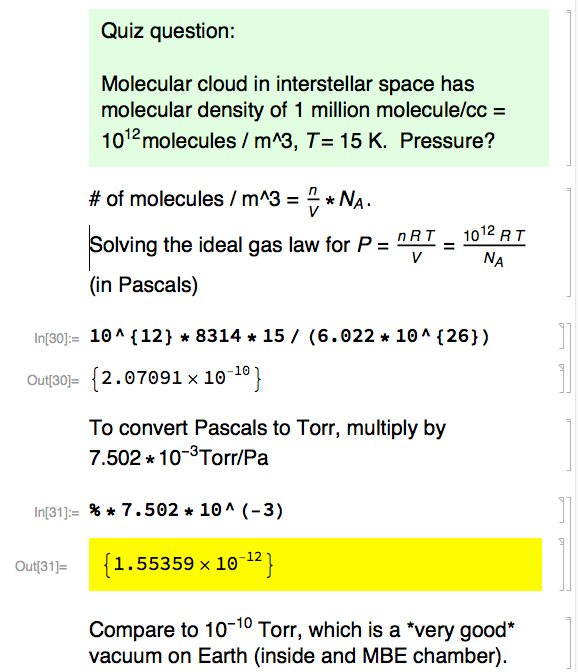
A quiz question from past years on pressure and number of molecules