Open systems
We've been living inside containers with a fixed quantity of material: $n=$constant. Now it's time to literally throw open the windows to the vibrant world outside of open systems...

... and read Chapter [9]!
By lifting the restriction to fixed $n$, we can start to deal with...
- Open systems exchanging materials with their surroundings,
- Phase transitions where one phase of a particular material changes into another phase of the same material, (OK, we have dealt with phase transitions a bit...),$$n_{\text{liq}},\ n_{\text{vap}}$$
- Chemical reactions, where one kind of material disappears and another appears.$$n_{H_2O},\ n_{H_2}, \ n_{O_2}$$
Single component
Even with only one kind of material (one "component") contained in a system, if the number of moles $n$ of material are allowed to change, then the internal energy $U(S,V)\to U(S,V,n)$ and the first law (the Pfaffian of $U(S,V,n)$) has to change: $$dU=T\,dS+P\,dV \to dU=T\,dS+P\,dV +\left(\frac{\del U}{\del n}\right)_{\color{red}S,V}\,dn$$
For each of the other three potentials, the extra term will be
$$...+\left( \frac{\partial H}{\partial n} \right)_{\color{red}S\color{black},P}dn, \ ...+\left( \frac{\partial F}{\partial n} \right)_{T,\color{red}V}dn, \ ...+\left( \frac{\partial G}{\partial n} \right)_{T,P}dn.$$
Each of $dU$, $dH$, and $dF$ involves calculating a partial derivative, while holding either $\color{red}S$ or $\color{red}V$ constant.
But $\color{red}S$ and $\color{red}V$ are extensive variables: They are proportional to the number of moles at hand. So it would be impossible to keep them constant while varying $n$! where
Only the Gibbs energy $G=G(T,P)$ is a function of only intensive variables, so we'll start with $G$, and hope to use the differential $dG$ to eventually tweak the other potentials to work with variable amounts of material.
Gibbs energy and chemical potential
We already know the functional dependence of $G$ on $n$. The Gibbs energy is: $$G(T,P,n)=n\,g(T,P),$$
where $g(T,P)$ is the specific Gibbs energy, per kilomole. We'll define the chemical potential $\mu$ as:
$$\mu \equiv \left( \frac{\partial G}{\partial n} \right)_{T,P} = g(T,P).$$
The last step uses the fact that $T$ and $P$ are intensive, and so are independent of $n$.
From the definition of $g$ in terms of a Legendre transformation of the internal energy, we had: $$dg = -s\,dT+v\,dP.$$
Using $G(T,P,n)=ng(T,P)$, we can figure the Pfaffian $dG$ as...
$$\begin{align}dG & = n\,dg + g\,dn\\
&=n(-s\,dT+v\,dP) +\mu\,dn\\
&=-S\,dT+V\,dP +\mu\,dn\end{align}.$$
The partial derivatives in our summary table for the 4 potentials could now be revised lightly to include the proviso that the number is also held constant, for example: $$-S = \left( \frac{\partial G}{\partial T} \right)_{P,n}.$$
Revising the internal energy
$G$ is related to $U$ through the Legendre transformation: $$G=U-TS+PV$$
which implies: $$dG=dU-T\,dS-S\,dT+P\,dV+V\,dP.$$
We just showed that $dG=-S\,dT+V\,dP+\mu\,dn$. Setting these two $dG$ expressions equal and solving for $dU$ gives... $$dU = T\,dS-P\,dV+\mu\,dn.$$
Where now, $\mu = \mu(S,V)$ is still the molar Gibbs energy, just written as a function of the extensive variables $V$ and $S$. Comparing with the Pfaffian of $U(S,V,n)$: $$\mu(S,V) = \left( \frac{\partial U}{\partial n} \right)_{S,V},$$
$\mu$ is apparently the change in internal energy per kilomole of material added at constant volume and constant entropy.
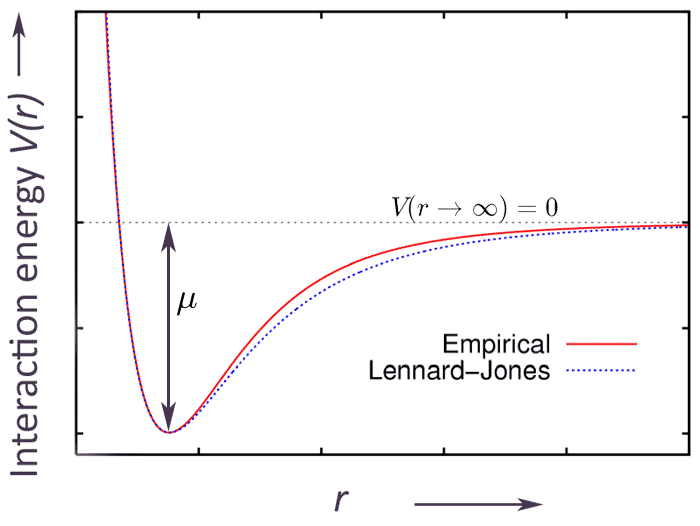
Carter argues that $\mu$ can be thought of as
- the depth of a Lennard-Jones-ish potential well
- for the average interaction energy, $V(r)$,
- between a new particle and the pre-existing "host" particles in the system.
Multiple components
With this picture in mind of adding small amounts of, say, Na${}^+$ or Cl${}^-$ ions to a water solution we note that as long as the concentrations of the ions remain small, then we don't have to change our assumptions about what the "host material" is: It's a good approximation to say it's still pure water.
For a single component, we had... $$dU = T\,dS-P\,dV+\mu\,dn.$$
If we add more than one thing to our solution, it seems like it shouldn't matter
- in which order we add ions,
- or whether we add a lot of sodium first, and then a little more, or vice versa.
So, this suggests that at constant $S$ and constant $T$, the change in internal energy on adding new things to a dilute solution is... $$[dU]_{S,V}=\mu_1 dn_1+\mu_2 dn_2+...$$
And so the general expression for $dU$ if we add $m$ different components to a system is
$$dU= T\,dS-P\,dV+\sum_{j=1}^m\mu_j\,dn_j.\label{dU}$$
Where
$$T=\left(\frac{\partial U}{\partial S}\right)_{V,\left\{n_j\right\}}
\ ,\ -P=\left(\frac{\partial U}{\partial V}\right)_{S,\left\{n_j\right\}}
\ ,\ \mu_j= \left(\frac{\partial U}{\partial n_j}\right)_{S,V,\left\{n_{j\neq k}\right\}}.
$$
All the differentials in this equation are extensive, and the coefficients of those differentials are intensive, which means that if we double the size of the system, while keeping the same composition, (that is, the same ratios of the $dn_j$'s), then the internal energy has got to double as well.
More generally, if we change the number of moles of each constituent
of the system by the same (small) fractional amount $\lambda$, that is $dn_j
= \lambda n_j$, then the total number of moles $n=\sum n_j$, and the volume,
entropy, and internal energy will also change by the same fractional amount:
$$dn = \lambda n
\ ,\ dV = \lambda V
\ ,\ dS = \lambda S
\ ,\ dU = \lambda U.$$
Substituting these expressions into the expression for $dU$ above, we have... $$\lambda U= T\,\lambda S-P\,\lambda V+\sum_{j=1}^m\mu_j\, \lambda n_j.$$
Dividing through by $\lambda$, $$ U= T\, S-P\, V+\sum_{j=1}^m\mu_j\, n_j.$$
A sneaky way (thanks Euler!) to get an integrated form of the internal energy.
Gibbs Energy for multiple components
Gibbs-Duhem equation
The integrated internal energy was: $$ U= T\, S-P\, V+\sum_{j=1}^m\mu_j\, n_j.$$
The differential is: $$dU = T\, dS +S\, dT-P\, dV-V\, dP+\sum_{j=1}^m\mu_j\, dn_j+\sum_{j=1}^m n_j\, d\mu_j.$$
Equating to our earlier result, ($\ref{dU}$), $dU= T\,dS-P\,dV+\sum \mu_j\,dn_j$, we get the
Gibbs-Duhem equation: $$S\, dT-V\, dP+\sum_{j=1}^m n_j\, d\mu_j=0.$$
This shows that the variations in intensive variables ($T$, $P$, $\mu_j$'s) are not independent. That is, like an equation of state, it is a constraint that reduces the overall number of independent variables needed to uniquely specify a system state.
Shortly we shall consider solids, liquids, gases, and different alloys coexisting in equilibrium with each other. We shall shamelessly exploit the Gibbs-Duhem equation.
Gibbs Energy expressions
The Gibbs Energy is defined as $G=U-TS+PV$, so, $$G=\sum_{j=1}^m\mu_j\, n_j.$$
The differential is: $$dG = \sum_{j=1}^m\mu_j\, dn_j+\sum_{j=1}^m n_j\, d\mu_j.$$
For constant pressure, constant temperature processes, Gibbs-Duhem says that the last sum vanishes, so $$[dG]_{T,P} = \sum_{j=1}^m\mu_j\, dn_j.$$
Image credits
Wikimedia user Poszwa, Finkelstein, Dorena WM