Clausius-Clapeyron equation
Consider a liquid-vapor system in a piston, in contact with a constant temperature reservoir, at a temperature below the critical temperature.
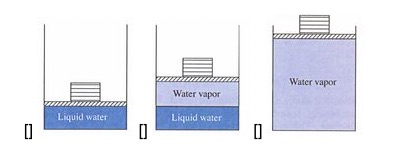
after Spakovsky
- Consider a Carnot cycle -- reversible adiabatic and isothermal processes,
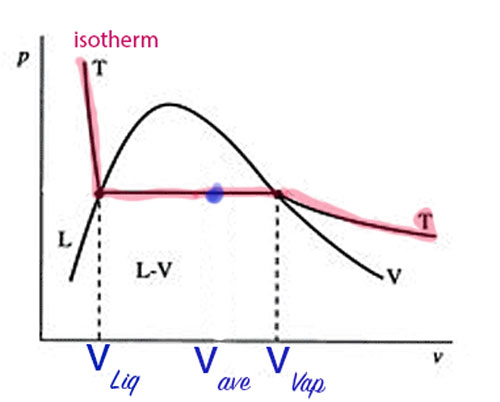
- But in a two phase system below the critical point: The isothermal process will be a horizontal line on a $P-V$ diagram.
- Will we still get the same efficiency as a Carnot cycle using and ideal gas?
- We'll find an equation for the slope the $P(T)$ coexistence curve: the Clausius-Clapeyron equation
- Solving problems with the Clausius-Clapeyron equation.
This material follows Spakovsky's treatment.
Carnot cycle with two phases
The efficiency of a Carnot cycle was $$\eta=\frac{T_2-T_1}{T_1}.$$ But we calculated it using an ideal gas. How universal is this? Would we get the same maximum efficiency for a different working substance? In particular, for a "binary phase": a pure substance in the two-phase coexistence region.
Here's the strategy map for what follows:
- We'll assume that the efficiency for a Carnot cycle with the binary phase *is* the same as what we calculated with the ideal gas.
- This assumption gives rise to the Clausius-Clapeyron equation: a differential equation that gives the slope (on a $P-T$ graph) of the coexistence curve.
- We'll look at experimental measurements of the slope.
- If the experimental results match our calculations, we'll take that as validation of the assumption of Carnot efficiency for a two-phase system.
The figure below shows a vanishingly small Carnot cycle $abcd$ in the liquid-vapor coexistence region. The heat absorbed at $T$ along the isotherm $ab$ depends on the number of kilomoles, $n$ of liquid which is vaporized, and the latent heat of vaporization $l$ (heat per kilomole): $$Q=nl.$$
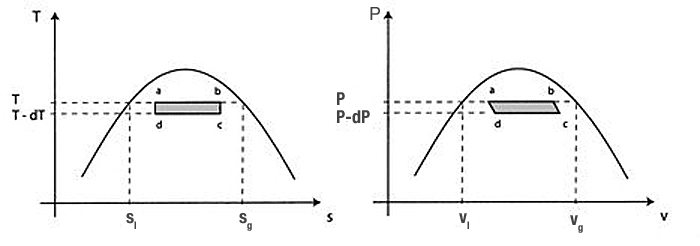
If the cycle shown has the Carnot efficiency, it is given by $$\eta = \frac{W}{Q_2} = \frac{Q_1 + Q_2}{Q_2} = \frac{T_2-T_1}{T_2},$$
and for this small Carnot cycle in particular... $$\frac{\delta W}{Q} = \frac{T-(T-dT)}{T} = \frac{dT}{T}.$$
Starting at $a$ we will heat the sytem to $b$. In this process, some of the liquid in the system, $n$ kilomoles, are converted from liquid to gas. (Along $cd$, $n$ kilomoles go from gas to liquid.) The volume change is $$\Delta V = n (v_g-v_l).$$ where $v_g$ ($v_l$) is the volume per kilomole of the gas (liquid).
Assuming that the work along $bc$ approximately cancels that along $da$, the remaining work is... $$\delta W = P n (v_g-v_l) -(P-dP)n (v_g-v_l) =n (v_g-v_l) dP.$$
Now, filling the pieces we've assembled into $\frac{\delta W}{Q}=\frac{dT}{T}$: $$\frac{n (v_g-v_l) dP}{n\,l}=\frac{(v_g-v_l) dP}{l} = \frac{dT}{T}.$$
Rearranging lightly, we get the Clausius-Clapeyron relationship
$$\frac{dP}{dT}=\frac{l}{T(v_g-v_l)}.$$
This is the slope of the vapor - liquid coexistence curve.
To integrate this, we need to know things like the temperature dependence of the heat of vaporization, and the molecular volume difference. Integration is doable if we make the following approximations:
- $l$ is approximately temperature independent (check out this assumption);
- The specific volume of the liquid is small compared to the gas, so that $v_g-v_l \approx v_g$;
- The vapor phase is an ideal gas, so $v_g = RT/P$;
With these approximations: $$\frac{dP}{dT}=\frac{l}{T(RT/P)}=\frac{lP}{RT^2}.$$
Rearranging and integrating... $$\begin{align}\int \frac{dP}{P} &= \frac{l}{R}\int \frac{dT}{T^2} \\ \ln P & = -\frac{l}{RT} + C.\end{align}$$
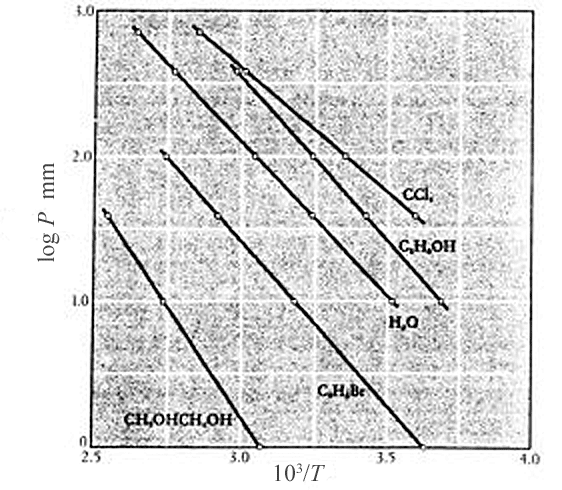 A plot of $\ln(P)$ vs $1/T$ for any number of substances in the two phase region (Mahan, 1963) appears to bear this out.
A plot of $\ln(P)$ vs $1/T$ for any number of substances in the two phase region (Mahan, 1963) appears to bear this out.
Or, $$P(T)=e^{-\frac l{RT}} + P_0$$ Here, in non-log coordinates, is $P(T)=e^{-1/T}$ (That is, $T$ is in units of $l/R$)...
Solving problems with the C-C equation
The integrated Clausius-Clapeyron equation $$\ln P = -\frac{l}{RT} + C$$ relates vapor pressure, the latent heat (enthalpy), $l$, of a phase transition and temperature.
Example
We know that the boiling point of water at 1 atm (= the vaporization pressure) occurs at 100 C. The latent heat at 100 C is $l$=40 kJ/mole. The gas constant is 8.314 J/(mole$\cdot$K) Calculate the vapor pressure of water at 90 C.
$$\begineq \ln P_2 -\ln P_1&=\frac{l}{R}\left( \frac{1}{T_1}-\frac{1}{T_2} \right)\\ \ln\left(\frac{P_2}{P_1}\right)&=\frac{l}{R}\left( \frac{1}{T_1}-\frac{1}{T_2} \right)\\ \frac{P_2}{P_1}&=e^{\frac{l}{R}\left( \frac{1}{T_1}-\frac{1}{T_2} \right)}\\ \Rightarrow P_2&=1\text{ atm}\exp\left[\frac{40\times 10^6}{8.314\times 10^3}\left( \frac{1}{373}-\frac{1}{363} \right)\right]\\ &=0.70 \text{ atm}.\\ \endeq $$
Using the same technique, we find that $P_{110 C}=$1.40 atm. So, you can see that $P(T)$ is not linear.
Match with data? [Graph of saturation curve]
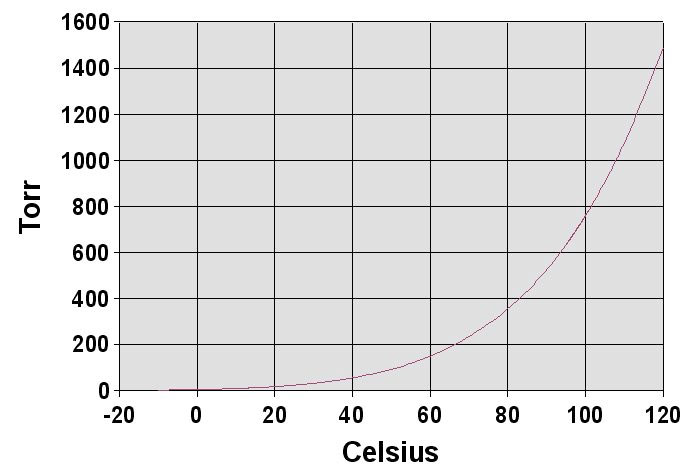
Image credits