Two-phase systems
The van der Waals equation of state resulted in
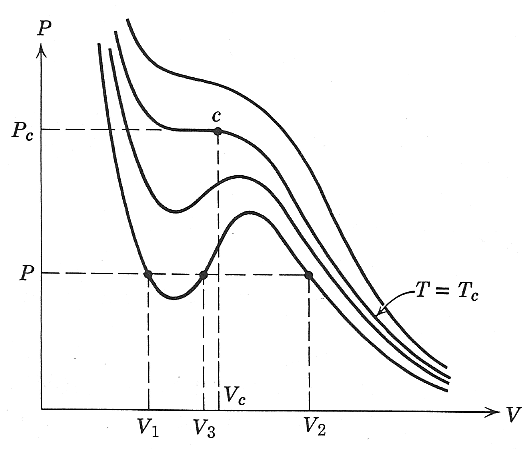
isotherms with a "kink" below a critical temperature $T_c$ and that, qualitatively, allowed for phase separation.
We will now get quantitative. In this topic and the next we will
- Qualitatively sketch the Helmholz energy, $[F]_T(v)$ of a van der Waals gas
- Use the sketch, together with the constraint of mechanical equilibrium to precisely locate the two molar volumes into which a van der Waals gas will separate.
- Show how coexisting phases are a key engineering solution to make heat engines with a high efficiency--that is, more nearly reversible.
- Calculate the slope of the coexistence curve for two phases.
Van der Waals phase transition re-visited
Paul talks through the Maxwell (equal area) construction for phase separation (24 minutes)
If two phases are in equilibrium with each other, (in equilibrium both thermally and mechanically) then they ought to have the same pressure and temperature. All the points on the same isotherm have the same temperature. A horizontal line at constant pressure in the diagram below can intersect an isotherm at as many as three points (as long as $T\lt T_c$). We have already argued that mechanical stability requires that $\del P/\del V \lt 0$ and so the phase with $V_3$ in the accompanying diagram is unstable.

So...if we start with volume $V_3$ at a temperature above $T_c$, and then cool, while keeping the volume constant, to a temperature below $T_c$, will the system separate into the two phases with $V_1$ and $V_2$ as indicated on the diagram, or will the pressure be somewhat higher or lower? How do we bring in the condition that the total free energy should be a minimum at equilibrium?
Let's start by sketching the free energy, $F(V)$, of the single phases represented by the van der Waals isotherms, as a function of volume. Since $[dF]_T = - PdV$, it appears that $$P=-\left(\frac{dF}{dV}\right)_T,$$ So, we can integrate $P$ along an isotherm to get the Helmholtz energy of a single phase by integrating the reversible work, $PdV$, along an isotherm: $$F=F_0+\Delta F = F_0 - \int (P\,dV).$$
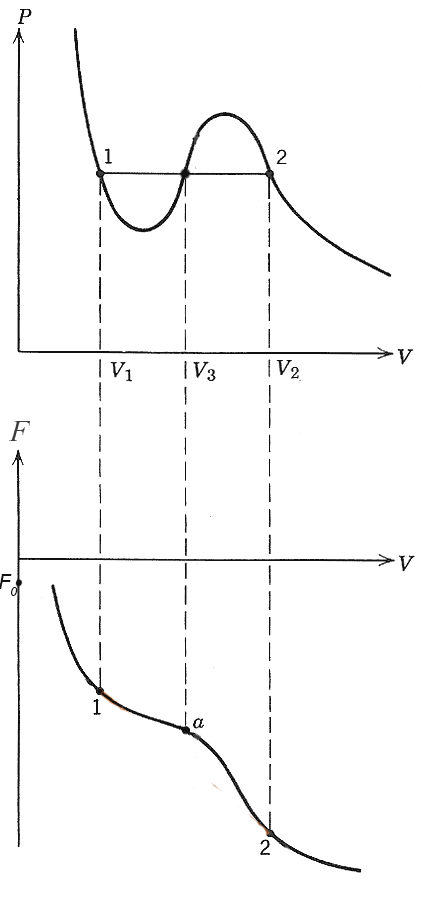 $F$ is a continuously decreasing function of $V$, since $P$ is always positive.
$F$ is a continuously decreasing function of $V$, since $P$ is always positive.
If you prefer, you can start with the bottom figure for $F$ and visually verify that the negative slope of that function is what is graphed as "$P$" in the top figure.
Lowest free energy
The criteria for an isochoric, isothermal system to be in equilibrium was that the free energy should be a minimum: as low as possible.
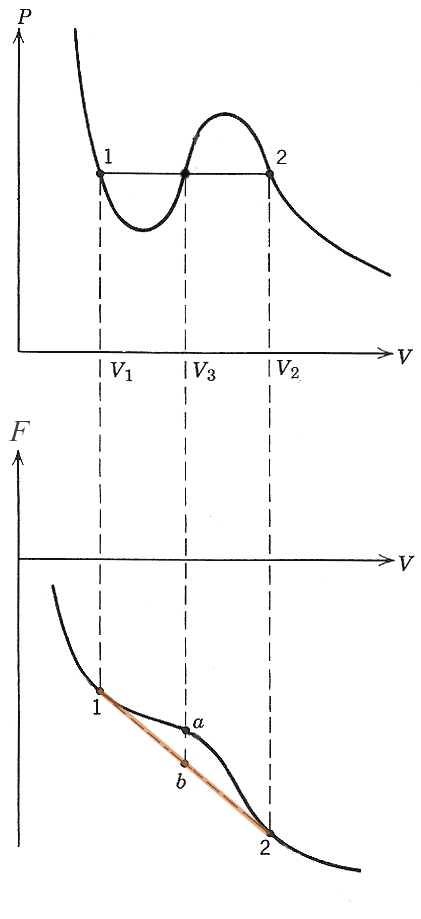
The orange dashed line segment on the Helmholz energy part of the graph is the free energy of a linear combination of the two phases at $V_1$ and $V_2$.
Since the Helmholz energy of any linear combination of 1 and 2 is always lower than any single-phase free energy between 1 and 2, the system can move to a lower total free energy by breaking up into a combination of the two phases at $V_1$ and $V_2$ (b) instead of staying at intermediate volume $V_3$ (a).
The pressure is also constant for all the linear combinations between 1 and 2, because the single phases 1 and 2 are at the same pressure.
Equal area construction
But what pressure are the two phases at? We will see that pressure line should be drawn such that the areas $A$ and $B$ shown are equal. This is the "Maxwell construction".
The conditions that determine 1 and 2 are:
- In order for the pressures to be the same, the slopes $\partial F/\partial V$ must be the same, because: $$\left.\frac{\partial F}{\partial V}\right|^{V=V_1} = -P_1 = -P_2=\left. \frac{\partial F}{\partial V}\right|^{V=V_2}.$$
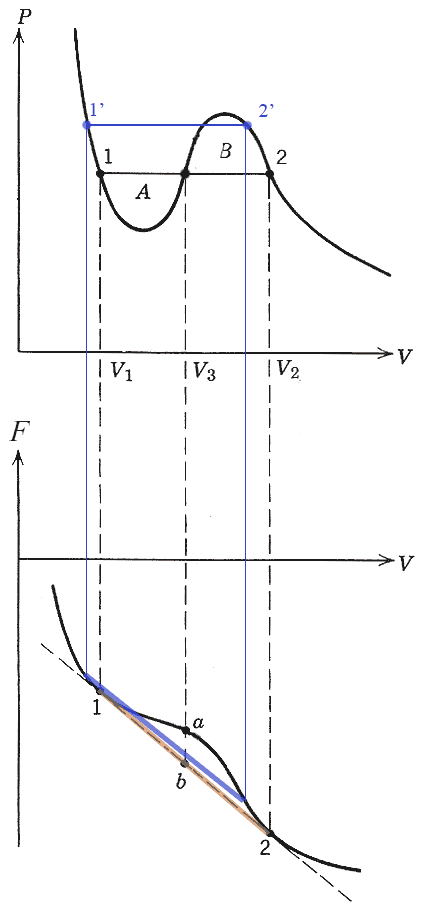 But points 1' and 2' also have the same pressure: Why not them?
But points 1' and 2' also have the same pressure: Why not them?
On the $F$ vs $V$ diagram...
The blue line segment shows the free energy of a linear combination of 1' and 2'. Tangent lines at 1' and 2' are parallel (same slope) but do not intersect.
The orange line segment shows the free energy of a linear combination of 1 and 2. Tangent lines at 1 and 2 are parallel (same slope) and *do* intersect. That is, they are on the *same* tangent line.
Points on the orange line segment are lower than any of the blue segments that connect other pairs of points with the same pressure.
$\Rightarrow$ The points for the two phases must lie on the unique line which is tangent to $F$ at two different points in order to get the lowest possible Helmholz energy for linear combinations.
Using the condition that the points lie on the *same* tangent line to $F$: $$\frac{F_2-F_1}{V_2-V_1}= \left(\frac{\partial F}{\partial V}\right)_{\text{at }V_1\text{ or }V_2}.$$
Rearranging a bit... $$-(F_2-F_1) = -\frac{\partial F}{\partial V}(V_2-V_1).$$
This is: $$\int_{V_1}^{V_2}P\,dV = P_1(V_2-V_1).$$
The terms on either side of this equation correspond to these areas on the graph:
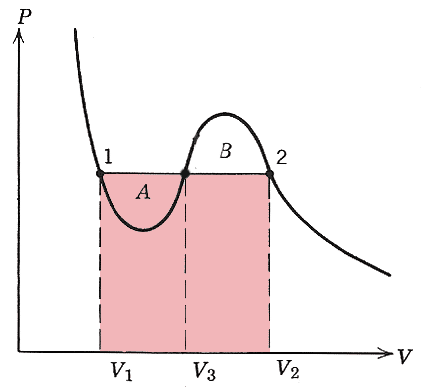 $$P_1(V_2-V_1)$$
$$P_1(V_2-V_1)$$
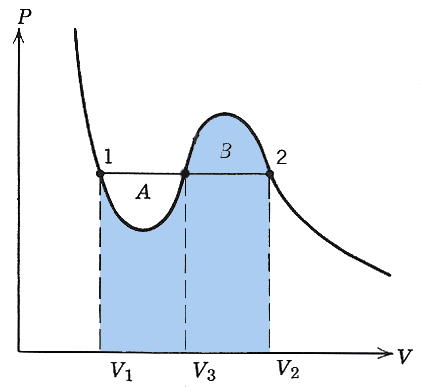 $$\int_{V_1}^{V_2}P\,dV$$
$$\int_{V_1}^{V_2}P\,dV$$
And Pink area= Blue area implies that the areas $A$ and $B$ are equal!
A further implication is that no matter what the initial molar volume of the system, *if* it phase separates, it will always phase-separate into the same two phases with $v_1$ and $v_2$ given by the equal area construction.
Image credits
Matthieu Marechal, Spakovszky, figure 8.6, Andrew Ainsworth, Mahan, Elementary Chemical Thermodynamics, 1963, cited in Spakovszky