Entropy changes and heat reservoirs
2014: I did the first two sections of this before the rest of the Gibbs Law topic because the examples are more accessible.
Consider connecting the two systems by a copper bar such that essentially *all* the heat is transferred. Compare at $\delta q/T_1$ and $\delta q/T_2$ (same \delta q).
But Spakovsky points out that you could connect them by a reversible Carnot engine instead and extract some of the energy as work reversibly.
An idealized heat reservoir...
- is at a constant, uniform temperature, and
- is in some sense 'large enough' that adding / subtracting heat (at least, "small" amounts) from it will not change its temperature appreciably.
Any large container of liquid is an approximation to such an ideal heat reservoir
Imagine transferring an amount of heat $\Delta Q$ into such a reservoir, and then out again. What is the net change in the entropy of this heat reservoir?
$$\Delta S = \oint \frac{\delta Q}{T} = \frac{\Delta Q}{T}-\frac{\Delta Q}{T}=0$$
There is no net change in the entropy of such a heat reservoir, so we say that an amount of heat $\Delta Q$ can be transferred in and out again reversibly.
The change in entropy of a heat reservoir when an amount of heat $\Delta Q$ is added to it ($\Delta Q > 0$) is: $$\Delta S = \frac{\Delta Q}{T}.$$
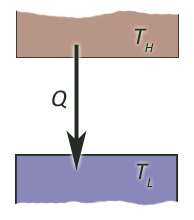
Heat transfer between two reservoirs
Now,
consider the process where an amount of heat $\Delta Q$ is transferred from a high
temp reservoir at $T_H$ to a lower temperature reservoir at $T_L$.
Imagine, for example, that they are connected by a copper bar which is an excellent conductor of heat...
The overall change in entropy is the sum of the entropy changes of the two reservoirs, and we have $$\Delta S = \frac{\Delta Q}{T_L} - \frac{\Delta Q}{T_H} = \Delta Q \frac{T_H-T_L}{T_H T_L}.$$
The change in entropy is positive when heat flows from the high- to the low-temp reservoir, but negative the other way.
So, the second law--that net entropy must increase for a spontaneous process--predicts correctly that heat will spontaneously (without any external work) flow from hot places to cold ones.
Obtaining work from a single heat reservoir
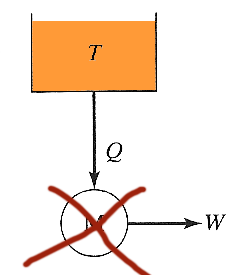Analyzing
the prohibited process where we try to extract heat from a single reservoir
and convert it to work... The net change in entropy is the sum of the changes
for heat reservoir, machine, and surroundings.
- Assuming the machine is run through a full cycle, it returns to its initial state and has no net change in entropy. (Entropy is a state function).
- The machine delivers no heat to the surroundings (only work), so the change in entropy of the surroundings is zero, so
$$\Delta S_t = \Delta S_{\rm res}+\Delta S_M+\Delta S_{\rm surr} = -\Delta Q/T + 0 + 0 = -\Delta Q/T.$$
Such a process is prohibited by the second law since the net change in entropy is negative.
Free expansion of an ideal gas
[Walls are not adiabatic]
The sudden free expansion of an ideal gas into a vacuum inside a closed
vessel is irreversible.
We used a reversible, isothermal expansion with the same initial and final conditions to calculate the change in entropy which was
$$\Delta S= nRT\ln\left( \frac{V_f}{V_i}\right).$$
For an expansion, $V_f > V_i$ so $\Delta S$ for the system is positive and $\Delta S_\text{surroundings}=0$. So the free expansion proceeds spontaneously. But a "free compression" would have a negative entropy change, and should not proceed spontaneously.
About entropy, Wikipedia sez ...
Entropy is a thermodynamic property that is the measure of a system's thermal energy per unit temperature that is unavailable for doing useful work.
Thermodynamic temperature
For a Carnot cycle running with an ideal gas as the operating medium, it was shown that
$$\frac{Q_1}{Q_2} = -\frac{T_1}{T_2}.$$
Taking into account the signs of the heats, this is the same as
$$ \frac{|Q_1|}{|Q_2|} = \frac{T_1}{T_2}.$$
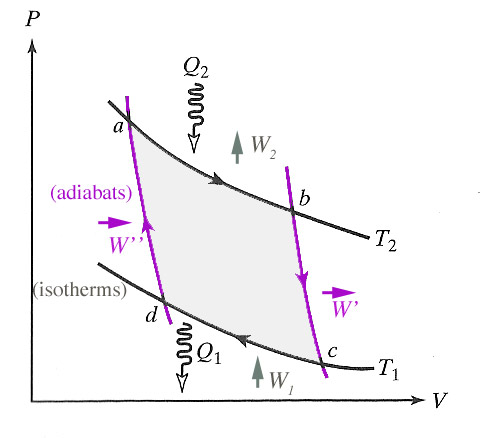
The fact that no heat engine has a higher efficiency than a Carnot engine hints that this relationship is perhaps more universal than our derivation using the ideal gas would suggest.
I will not prove this result (see Carter's chapter 6, section 7 or Spakovszky), but the ratio of heats in a Carnot engine can in fact be used as the empirical basis for a temperature scale without having to assume that the working substance is an ideal gas. Then in terms of some experimentally easy-to-define reference temperature $T_{\rm ref}$ (=273.16 K: the triple point of water), the thermodynamic temperature is defined as this ratio of the heats absorbed and given off at the two isotherms:
$$T=T_{\rm ref}\frac{|Q|}{|Q_{\rm ref}|}.$$
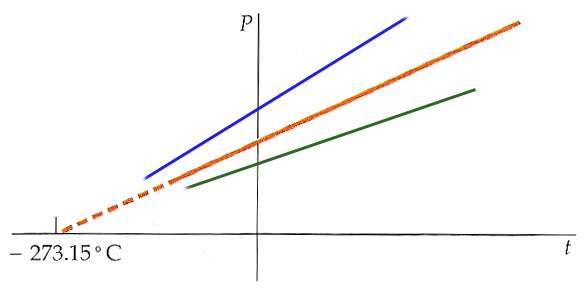
This suggests an absolute zero as the temperature at which there is no heat flow for an isothermal compression. This does indeed coincide with the $P\rightarrow 0$ extrapolation for nearly-ideal gases.
