Combining the first and second laws
Pulling together some characteristics of entropy
- $S$ is a function of the state of the system. So we can write it as a function of any two state variables / functions, for example, $S=S(T,P)$, or $=S(T,V)$, or $=S(P,V)$, or sometimes even $S=S(U,P)$.
- Entropy $S$ is extensive. Specific entropy $s=S/n$ is intensive. (BTW $S/m$ is also intensive)
- Units for $S$ are Joules / Kelvin.
- In a reversible system, $dS = \delta Q_r / T$.
Spakovszky's definition of reversibility:
A process is called completely reversible if, after the process has occurred, both the system and its surroundings can be wholly restored by any means to their respective initial states.
The first law and the second law, together
[Big picture:] Systems may interact with their surroundings (and exchange energy, $\Delta E$) by
- doing electrical work
- magnetically
- changes of gravitational energy
- ...etc, etc
But, if we limit our attention to systems that interact with their surroundings only through exchanges of heat, $\delta Q$, and mechanical work, $\delta W$, we have
$$dU = \delta Q - \delta W.$$
which is Always true....Sometimes true: in the case of reversible work: $$\delta W = \delta W_r= P\,dV.$$ $$dU = \delta Q - P\,dV.$$
Sometimes true: for reversible heat: $$\delta Q=\delta Q_r = T\,dS.$$ $$dU = T\,dS - \delta W.$$
How general is this statement of the first law if we use the reversible expressions for work and heat to write $$dU = T\,dS - P\,dV \ ??$$
It's certainly true for reversible processes.
But, hmmm, *all* the quantities in this equation are state variables or state functions of the state
so we conclude (are *forced* to conclude!) that this statement is always true:
Gibbs' Law $$dU = T\,dS - P\,dV.$$
[Gibbs Law] is by far the most important relation in classical thermodynamics. -Ashley Carter
Free expansion and isothermal expansion
Regarding the reading questions on Spakovsky...
Q: We noted that the entropy change, $\Delta S$, for both free and isothermal expansion was exactly the same. And that heat was absorbed in the isothermal expansion but not in the free expansion. What about figuring $\Delta S=\int\frac{\delta Q}{t}$? How can both final states have the same entropy when one has absorbed heat and the other hasn't?
A: That integral only works for reversible processes. The correct expression is: $$\Delta S=\int \frac{dQ_r}{T}.$$
Along these lines, Carter also notes, when talking about Gibbs' law ($dU=T\,dS-P\,dV$) vs the first law ($dU=\delta Q-\delta W$), which are both universally true...
It's just that $\delta Q$ is identifiable with $T\,dS$ and $\delta W$ with $P\,dV$ only for reversible processes.
My head hurts from thinking about this so abstractly. Is there an atomic way of thinking about the difference between these two kinds of expansions?
Microscopically, we will find that $\frac12m\langle v^2\rangle \propto k_B T$: Temperature is a measure of the average kinetic energy of molecules (ahem... and eventually rotational kinetic energy and...)
Let's assume that the walls and pistons are all rigid, and all collisions are elastic...
Do problems 6-7a and 6-8a.
Entropy changes for some reversible processes [7.1, 7.2]
We figured out expressions for the work done in isochoric, isobaric, etc.... processes. Now let's do the same thing for the entropy change in different processes.
Gibbs law holds for all kinds of processes, but for reversible processes can be written: $$dU = T\,dS-P\,dV = \delta Q_r - P\,dV.$$
Adiabatic process: $$\delta Q_r = 0 \Rightarrow dS =\frac{\delta Q_r}{T}= 0.$$ So, this is an isentropic process.
(However, there are also irreversible, adiabatic processes, such as rapid, free expansion.)
Isothermal process: $$\Delta s =s_2-s_1= \int \frac{dq_r}{T} = \frac{\Delta q_r}{T}.$$ (Sometimes you'll see this written as just $q_r/T$.)
Carnot cycle:
Consists of reversible adiabatic compressions/expansions and isothermal compressions/expansions. [Graph a Carnot cycle on a $T$ vs $s$ plot.]
The adiabatic parts of a Carnot cycle are reversible, so from the above considerations we conclude these are isentropic (constant entropy). The graph of a Carnot cycle on a $T-s$ plot is then a very simple figure...
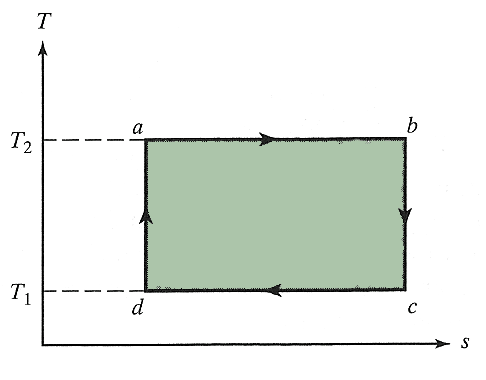
The area under a process line on a $T-s$ plot corresponds to...what??
$$\int T\,ds = \int T\left(\frac{\delta q_r}{T}\right)=\int \delta q_r = q_r.$$
So, apparently the shaded area on this $T-s$ Carnot plot is... $$q_2+q_1 = w.$$
Phase change:
If a phase change (e.g. ice, melting to water) takes
place in an open container, it is isobaric as well as isothermal.
The heat absorbed (or given off) per kilomole is the latent heat $l$, so we conclude that the change of entropy is... $$\Delta s = \int \frac{\delta q}{T} = \frac{l}{T}.$$
Isochoric process:
Normally $u=u(v,T)$. For an isochoric process, $u=u(T)$ and that means $du
= c_v\,dT$. Since $dv=0$, the first law reads $du=\delta q$.
If $c_v$ is independent of temperature, then $\Delta s = c_v\ln\left(T_2/T_1\right)$.
Isobaric process:
For reversible processes, the enthalpy is convenient, since...
$$dh = du+Pdv+vdP=\delta q_r -Pdv+Pdv+vdP=\delta q_r+vdP.$$
For an isobaric process, $h=h(T,P) = h(T)$ and $dh = c_P\,dT$. Dividing by $T$: $$\Delta s = \int_1^2 c_P \frac{dT}{T}.$$
When $c_P$ is constant over this temperature range, $$\Delta s=c_P\ln\left(T_2/T_1\right).$$
Entropy changes for an ideal gas [7.4]
Making no assumptions of reversibility, the Gibbs relation still holds... $$du = Tds-Pdv.$$
For an ideal gas, the internal energy is only a function of $T$, so $du = c_v\,dT$... $$c_v\,dT = T\,ds-P\,dv \Rightarrow ds= c_v\frac{dT}{T}+\frac{P}{T}dv.$$
Using the ideal gas law to write $P/T = R/v$: $$ds = c_v\frac{dT}{T}+R\frac{dv}{v},$$ which relates the fractional temperature and volume changes to entropy changes.
We can write this in terms of $P$ and $v$ instead of $T$ and $v$ by the following trick: Take the natural log of the ideal gas law:
$$\ln P +\ln v= \ln R + \ln T.$$Taking differentials... $$\frac{dP}{P}+\frac{dv}{v} = \frac{dT}{T}.$$
Subbing this equation for $dT/T$ in our $ds$ expression: $$\begin{align}ds = & c_v\left( \frac{dP}{P}+\frac{dv}{v} \right)+R\frac{dv}{v} = c_v \frac{dP}{P}+\left( c_v + R\right)\frac{dv}{v}\\ = & c_v \frac{dP}{P}+ c_P\frac{dv}{v} \end{align}$$
Using $c_P/c_v = \gamma$, $$\frac{ds}{c_v} = \frac{dP}{P} + \gamma\frac{dv}{v}.$$
Integrating from state 1 to state 2:
$$\frac{\Delta s}{c_v} =\ln\left( \frac{P_2}{P_1}\right) + \gamma \ln\left( \frac{v_2}{v_1}\right) = \ln\left( \frac{P_2v_2^\gamma}{P_1v_1^\gamma}\right).$$Taking $e^\left(...\right)$ of both sides... $$\frac{P_2v_2^\gamma}{P_1v_1^\gamma} = e^{\Delta s/c_v}.$$
This expression is good for ideal gases in both reversible and irreversible processes.
We previously found this relationship for an adiabatic process, for an ideal gas: $$Pv^{\gamma} = K.$$
Now we see in a deeper way, that this result is true for any isentropic process with an ideal gas.