The Second Law
Thou shalt read Chapter 6!
A new state variable?
The first law reads... $$dU = \delta Q - \delta W.$$
Our work expression for reversible systems is $$\delta W_r=P\,dV.$$ Re-arranging this to solve for the exact differential $dV$: $$\frac{1}{P}\delta W_r=dV.$$
In other words, the inexact differential, $\delta W_r$, can be made into an exact differential, by multiplying by an integrating factor, $1/P$ to give an exact differential.
Wouldn't it be nice if we could do the same with the inexact differential $\delta Q$?
Notice further that
- $W$ and $V$ are extensive quantities,
- the integrating factor $1/P$ is intensive.
$T$ is the other intensive thermodynamic parameter that we have, so following the same pattern, perhaps...
$$\frac{\delta Q_r}{T} \equiv dS$$ ...could turn out to be an exact differential? $S$ would then be an extensive variable, with units of Joules / ${}^o$K.
And then we could write the first law in terms of exact differentials...$$dU=T\,dS-P\,dV$$ ?!?!
It will turn out that this *is* the case, and $S$ is called entropy.
Entropy: a state variable
To show that $dS = \delta Q_r / T$ is an exact differential, we would have to show that it is path independent.
OK, let's show that it is path independent, at least for reversible processes:
If a quantity is path independent, then its integral around any path (like the black one in the figure...) should vanish.
$$\oint dS = \oint \frac{\delta Q}{T}\stackrel{?}{=} 0.$$
In a calculus-ey fashion, we can approximate the path around some arbitrary, reversible path with a line of ever smaller zigs and zags along isotherms and adiabats.
- Along all the adiabatic paths, no heat enters, or leaves the system, so $\Delta Q/T=0/T$ so no contribution...
- we only need to count up the $\Delta Q/T$ amounts along the isothermic parts of each zig-zag.
The heat entering (or leaving) the system along isotherm segment $i$ is $\Delta Q_i$ at temperature $T_i$, and we have... $$\lim_{\Delta Q_i \rightarrow 0} \sum \frac{\Delta Q_i}{T_i} = \oint \frac{\delta Q}{T}.$$
For each isotherm segment directed to the right along the top of the path, there is a corresponding isotherm segment along the bottom of the path that, together with their connecting adiabats, form a narrow Carnot cycle [adiabat, isotherm, adiabat, isotherm]. And we saw that the heats entering and leaving a system running in a Carnot cyle are in the ratio: $$\frac{\delta Q_1}{\delta Q_2}=-\frac{T_1}{T_2}.$$
This relation implies that $$\frac{\delta Q_1}{T_1}+\frac{\delta Q_2}{T_2}=0.$$
That is... the little change in entropy at the top of a Carnot cycle exactly cancels the change at the bottom:
Since we can divide up the whole cycle in terms of Carnot cycles with matching top and bottom contributions, we conclude that
$$\oint \frac{\delta Q_r}{T} = \oint dS =0$$
...for any reversible path, and this proves that $dS=\delta Q_r/T$ is an exact differential.
$$\Delta S = \int \frac{\delta Q_r}{T}$$ where $\delta Q_r$ is the heat that enters (leaves) the system, and the $r$ is there to remind you that this result only holds along a reversible path.
What does it mean that $dS$ is exact??...
$S$ is a state variable or 'coordinate'. So, any state has a unique entropy, no matter how we got there. Any point in a PV diagram has a unique entropy. We'll use that in a minute.
Entropy changes in irreversible cycles
All irreversible processes have an efficiency $\eta ' < \eta_r$ less than the efficiency of a reversible process. In terms of the heats: $$\frac{Q_1'}{Q_2'} < \frac{Q_{1r}}{Q_{2r}} = -\frac{T_1}{T_2}.$$
This implies that for one of our narrow, strip-like cycles used to tile the process, that $$\frac{\delta Q_2'}{T_2} + \frac{\delta Q_1'}{T_1} < 0.$$
Covering the (at least partially) irreversible cycle and integrating as before, we find that $$\oint \frac{\delta Q'}{T} < 0.$$
To be very general, we could summarize things this way, in the form of the Clausius inequality:
$$\oint \frac{\delta Q}{T} \le 0.$$
The equal sign holds for reversible processes. This is the content of the second law of thermodynamics.
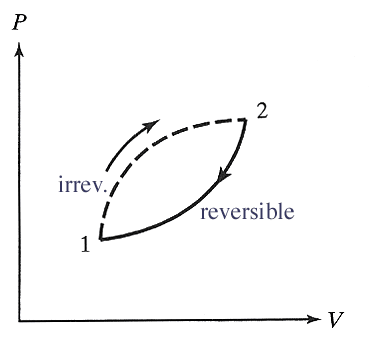Applying this inequality to the path in the accompanying diagram, we conclude...
$$\int_1^2 \frac{\delta Q}{T} \le \int_1^2 \frac{\delta Q_r}{T}=\int_1^2 dS = S_2-S_1=\Delta S.$$
Or in differential form: $$\frac{\delta Q}{T} \le dS.$$
This is parallel to the result for work, where... $$ P_s\,dV \ge \delta W. $$ "The work done by the system is greater than or equal to the work done on the surroundings." The equal sign only holds for reversible processes.
Isolated system: No heat enters or leaves an isolated system, so $\delta Q = 0$. From the inequality above, we expect that $$\int_1^2 dS = \Delta S \ge 0.$$
In words...
The entropy of any isolated system increases in any irreversible process, or remains unchanged for any reversible process.
Note that this is the net entropy, not the entropy of each and every part of a system.
Read:
- Carter, section 6.6: There exists no process that can increase the available energy in the universe.
- Spakovszky, The difference between free expansion... and reversible isothermal expansion.