Carnot cycle

A heat engine is a thermodynamic system which moves through a complete cycle ($\Delta U = 0$).

• What's the maximum efficiency of such an engine? Let's consider a reversible system: with no friction.
• In order to make some calculations, let's work with a substance we understand thoroughly: an ideal gas.

These characteristics are why we consider the Carnot Cycle

Our goal is an expression that relates efficiency to the temperatures, $T_1$ and $T_2$, of the heat reservoirs (instead of the heats, $Q_1$ and $Q_2$).

The Carnot cycle consists of only reversible processes:

• $a\rightarrow b$ isothermal expansion,
• $b\rightarrow c$ adiabatic expansion,
• $c\rightarrow d$ isothermal compression,
• $d\rightarrow a$ adiabatic compression.

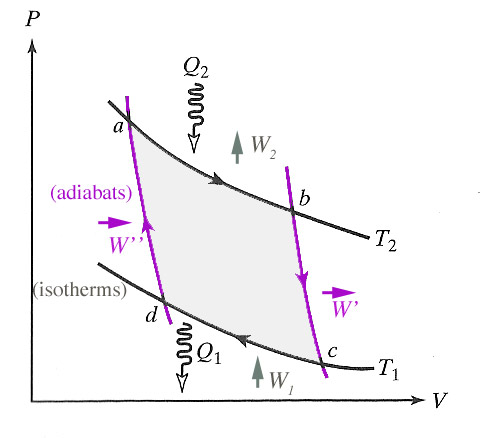
The total work that the system does on its surroundings is: $$W = \oint P\,dV = W_2 + W' + W_1 + W''.$$ By the way, this corresponds to the area on a $P-V$ diagram enclosed by the cycle's path.

We can calculate the efficiency explicitly for the case that the Carnot cycle is carried out on an ideal gas:

Isothermal paths

Along the two isotherms, since there's no temperature change, the internal energy is not changing along the path, so... $$0 > Q_1 = W_1 = nRT_1\ln\left(\frac{V_d}{V_c}\right).$$ $$0 < Q_2 = W_2 = nRT_2\ln\left(\frac{V_b}{V_a}\right).$$ (Here's where we calculated the work for an isothermal process.)

Adiabatic paths

We saw that for an ideal gas, $PV^\gamma=K$. Subbing in the ideal gas expression for pressure, $P=nRT/V$, we have $nRTV^{\gamma -1}=K$. $b$ and $c$ are on the same adiabat (same $K/(nR)$), so... $$T_2V_b^{\gamma-1}=T_1V_c^{\gamma -1}.$$

$a$ and $d$ also share an adiabatic path, so: $$T_2V_a^{\gamma-1}=T_1V_d^{\gamma -1}.$$

Putting these two equations together... $$\begineq \frac{T_2V_b^{\gamma -1}}{T_2V_a^{\gamma -1}} &= \frac{T_1V_c^{\gamma -1}}{T_1V_d^{\gamma -1}}\\ \left(\frac{V_b}{V_a}\right)^{\gamma -1} &= \left(\frac{V_c}{V_d}\right)^{\gamma -1} \\ \frac{V_b}{V_a} &= \frac{V_c}{V_d} \endeq$$

Putting this together with the heats calculated from the isotherms, $$\begineq\frac{Q_1}{Q_2} &= \frac{nRT_1 \ln\left(\left(\frac{V_b}{V_a}\right)^{-1}\right)} {nRT_2 \ln\left(\frac{V_b}{V_a}\right)} \\ &= -\frac{T_1}{T_2}. \endeq$$

For an ideal gas, running in a Carnot cycle (adiabats and isotherms), the efficiency is: $$\eta = 1+\frac{Q_1}{Q_2} = \color{blue}1- \frac{T_1}{T_2}.$$

Carnot refrigerator / heat pump

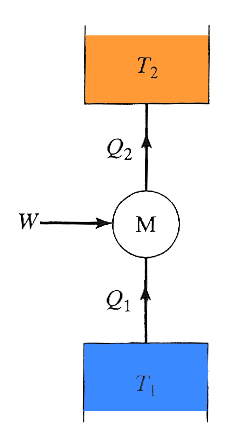A Carnot engine run backwards will remove heat from a cold temperature reservoir and dump heat at a higher temperature. This is exactly what you'd want in a refrigerator. Here, the measure of efficiency (called the coefficient of performance, $c$) is how much heat can be extracted ($Q_1$) per amount of work invested. In order to make this a positive number... $$\begineq c_{\rm ref} & \equiv -\frac{Q_1}{W} \\ & = -\frac{Q_1}{Q_1+Q_2} = -\frac{Q_1}{Q_1 - T_2 Q_1/T_1} \\ & = \frac{1}{(T_2-T_1)/T_1} = \frac{T_1}{T_2-T_1}.\endeq$$

Unlike the efficiency, it's quite possible that $c_{\rm ref} > 1$.

For refrigerators, we want to maximize amount of heat removed from the cold reservoir.

Heat pumps run the same cycle as refrigeration, pulling heat out of a cold reservoir and dumping heat into a hot reservoir. But we want to maximize the amount of heat transferred into the hot reservoir.

Our 'efficiency' measurement is now: $$c_{\rm hp} = -\frac{Q_2}{W} = \frac{T_2}{T_2 - T_1}.$$ And this number can exceed 100% ! ! !

Cartoon view of the refrigeration cycle

How do they work?

Expansion/compression of gases

Both of these devices take advantage of this behavior exemplified by gases in our compression cylinder:

• If you suddenly (adiabatically) compress a gas, its temperature will rise dramatically.
  
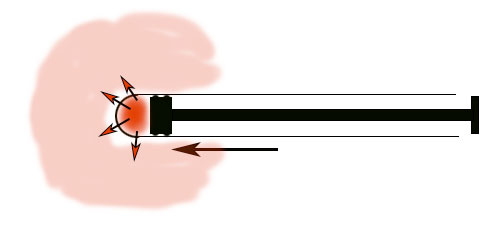
• Conversely, if you force a gas to suddenly expand (adiabatically), its temperature will drop dramatically.
  
  

Refrigerator

• Take your gas cylinder inside a fridge.
• Quick! Use mechanical energy to expand the gas!
  
  The expanded gas is colder than the fridge, so,
• - Heat flows from the fridge to the colder piston gas,
  - until the fridge and piston gas temps are equal.
  
  
• Take your gas cylinder to the room outside.
• Quick! Compress the gas!
  
  The gas is hotter than the room, so
• - Heat flows from the hot piston gas to the air in the room,
  - until the room and piston gas temps are equal.
  
  
• Repeat!

Heat pump

Heating your house (warm reservoir) in winter, by pumping heat in from the outside (cold reservoir)...

• Take your gas cylinder outside the house.
• Quick! Expand the gas!
  
  The expanded gas is colder than the air outside, so,
• - Heat flows from the outside air into the colder piston gas,
  - until the piston gas reaches the outside air temperature.
  
  
• Take your gas cylinder inside the house.
• Quick! Compress the gas!
  
  The gas is hotter than the room, so
• - Heat flows from the hot piston gas to the air in the room,
  - until the room and piston gas temps are equal.
  
  
• Repeat!

Does it matter if the outside temperature is cooler than the inside temperature??

The gas piston acts like a "bucket for heat" tranferring heat from one place to another. Thisness of a that

Functional diagram of the refrigeration cycle: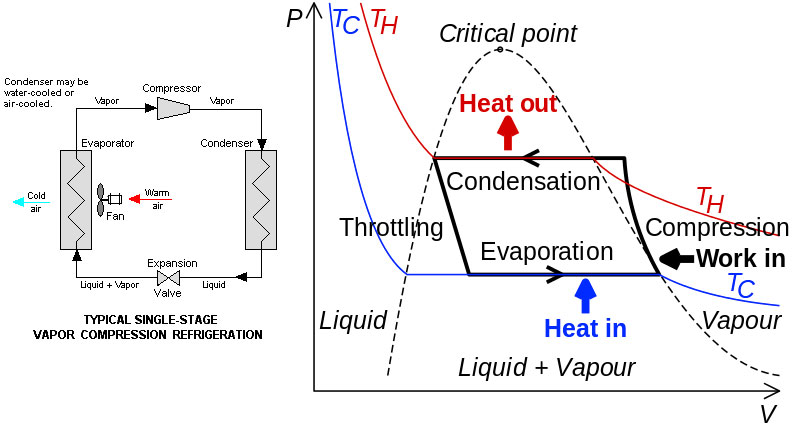

Actual refrigerators / heat pumps actually circulate a chemical that has a boiling temperature somewhat higher than room temperature and operate in the liquid-vapor coexistence region. The phase transition allows a large amount of heat (the enthalpy of the change of state) to be absorbed / emitted in each cycle, without a large difference in temperature.

And the coefficients ('efficiencies') of both heat pumps and refrigerators... $$c\propto \frac 1{T_2-T_1}$$ So a smaller temperature difference is more efficient!

HVAC lingo

In the U.S. you will hear (at least) three different measures of energy efficiency for air conditioners and heat pumps...

See...

• Carrier heat pump comparison
• Heat pumps in Wikipedia

COP

COP = coefficient of performance is, as above, a dimensionless ratio of cooling power to (mechanical) energy input power.

EER

EER = energy efficiency ratio

Historically, cooling power has been measured in BTU/hr, and electrical power in Watts. The EER is a ratio of cooling power to electrical power input with units of BTU/W$\cdot$hr. You can convert to COP, by using...

1 BTU / 1 Watt$\cdot$hr = 0.29.

A unit with a (S)EER of 13 has a COP of about 3.4.

SEER

SEER = seasonally adjusted energy efficiency ratio

As is evident from our discussion of the Carnot 'fridge, the COP depends on the two temperatures $T_1$ and $T_2$. The SEER is an attempt to get an average efficiency over the whole season. It has the same units (BTU/Watt$\cdot$hr) as EER.

For heat pumps, the Heating Seasonal Performance Factor (HSPF) is the total heat delivered (in BTU) over the course of a year divided by the total input energy (in kWh) over the year. The comparisons offered for different models are for some ANSI-defined "average climate" for the U.S., so actual HSPF in Minnesota would be slightly worse than Arkansas.

The dimensionless coefficient of performance for a heat pump is derived by multiplying HSPF * (0.293 W*h / 1 BTU).

[Heat pump vs furnace comparison writing assignment]

Real engines

Here is an idealized Otto cycle--the most common automobile gasoline engine.

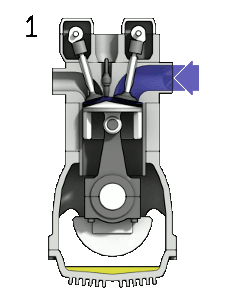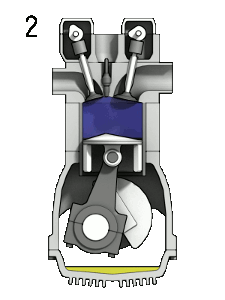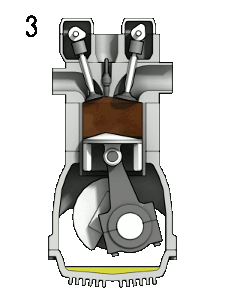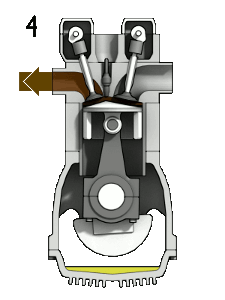
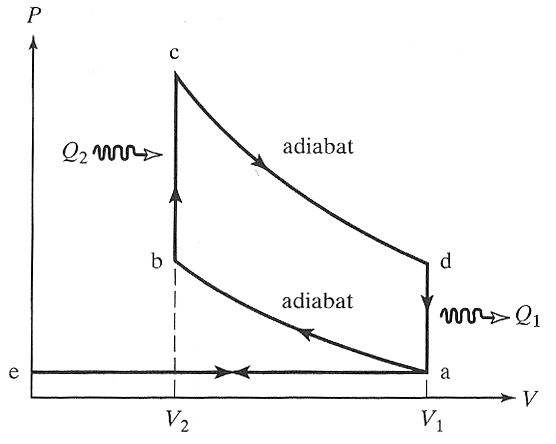
In problem 5-14 it's shown that... $$\eta = 1-\frac{T_d-T_a}{T_c-T_b}=1-\frac{1}{(V_1/V_2)^{\gamma - 1}}.$$

So, to increase efficiency, you'd like to increase the compression ratio $(V_1/V_2)$. But go too high and you run into pre-ignition: the fuel-gas mixture lights up before the spark comes.

The diesel engine gets around this by compressing only air (no fuel) to well above the ignition temperature, and then spraying fuel into the hot cylinder.

Image credits