Heat engines
How to generate (almost all of the) electricity in the U.S.A.
Isothermal vs Adiabatic compression: $v^{-1}$ vs $v^{-1.4}$.
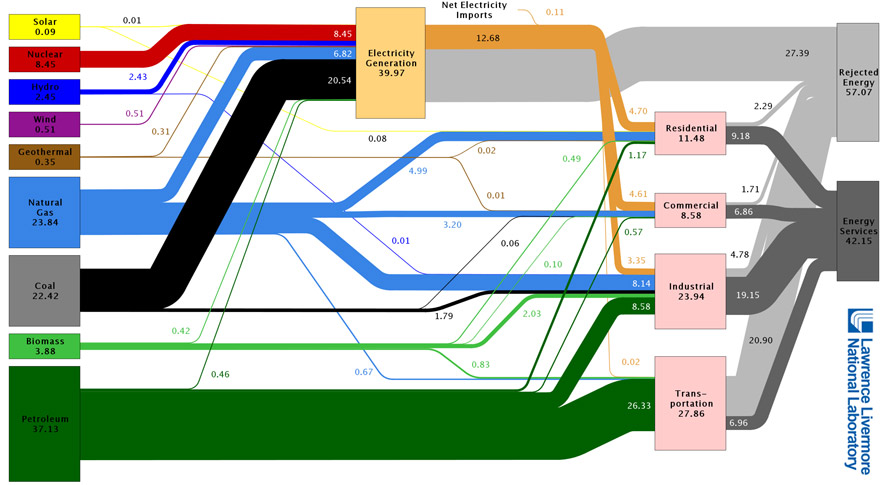
Some quick (and somewhat sobering) calculations: What is the average U.S. efficiency (useful energy output / energy input) of:
- Electric generation: The orange bar is useful electric energy delivered (the gray bar is "rejected" energy), which can be compared to the 39.97 Quads of energy consumed / input.
- The transportation sector: The dark gray bar is the energy that goes into moving cars/trucks/buses forward.
Vast majority of electricity generated like this:
- chemical bonds are rearranged (burned), or nuclear bonds are rearranged (nuclear reactor) to generate heat
- heat is used to boil water and generate steam
- ...to drive an electric generator
Vast majority of transportation is powered by (internal combustion engine - "ICE"):
- chemical bonds are rearranged to generate heat
- heat is used to expand a gas; push a piston
- $\to$ turn wheels to move a vehicle forward
Vast majority of heating homes is powered by:
- combustion (heat): coal/natural gas
Heat is *not* an intermediate stage with a minority of industrial processes:
- Photovoltaic panels
- electric motors use DC
What about trains? nuclear submarines? electric vehicles? the human body?]
It turns out that there are fundamental limits to how much energy can be converted from heat energy to mechanical energy (work).
Changing heat $\Leftrightarrow$ work
The heat engine is a useful abstraction consisting of...
- a system,
- that does mechanical work,
- can exchange heat with constant temperature heat reservoirs.
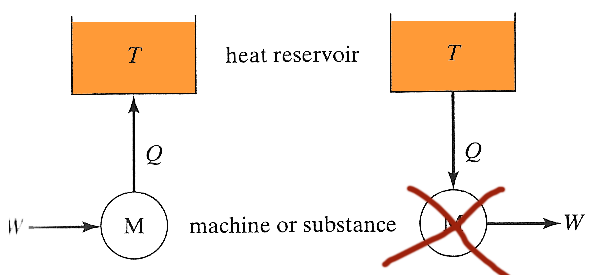
In what sense is a gasoline engine a "heat engine"?
The simplest possible heat engine (shown schematically as a machine by the M) on the left has work done on it, and converts all the work to heat, which is dumped into a heat reservoir.
The process on the right involves a machine which absorbs heat and converts it completely into work. Such a heat engine...
- is not prohibited by the laws of mechanics,
- is not prohibited by the first law (conservation of energy),
- but has never been found to exist,
- $\Rightarrow$ This 'nonexistence' is codified in the second law of thermodynamics.
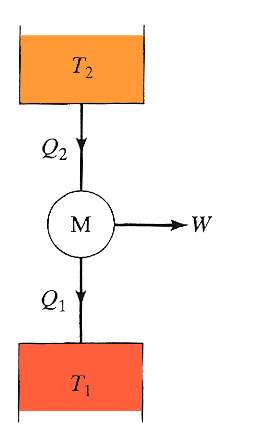 A more
realistic heat engine that converts some of the heat it absorbs to work can
be depicted as shown here. It absorbs heat from one reservoir at $T_2$, performs
an amount of work $W$, and dumps (rejects) heat to a reservoir at a different temperature $T_1$, where
$T_2 > T_1$.
A more
realistic heat engine that converts some of the heat it absorbs to work can
be depicted as shown here. It absorbs heat from one reservoir at $T_2$, performs
an amount of work $W$, and dumps (rejects) heat to a reservoir at a different temperature $T_1$, where
$T_2 > T_1$.
The fraction of the input energy (only heat $Q_2$) that is converted $\to$ work $$ \eta = \frac{W}{Q_2}.$$ This is called 'efficiency' and $\eta$ is pronounced 'eta'.
Using the first law, for a system that makes a complete cycle, $$\Delta U = 0 = Q_1 + Q_2 - W.$$
So the efficiency can also be written... $$\eta = \frac{Q_1+Q_2}{Q_2} = 1+\frac{Q_1}{Q_2}=1-\frac{|Q_1|}{|Q_2|}.$$ ...remember that heats are positive when they enter a system system,
Therefore for the system $M$, $Q_2 > 0$, but $Q_1 < 0$.