Ideal vs Non-ideal gases
Idealized and non-idealized (more realistic!) gas images...

...in to Chapter 5. Goals for today
- To understand how real gases differ from ideal gases.
- To understand how the roles of $a$ and $b$ in the van der Waals equation of state in modelling realistic gases.
Ideal gas
[diagram of ideal gas vs T]
In thermodynamic terms, an ideal gas is a substance for which $u=u(T)$, that is, $(\partial u/\partial v)_T=0$.
In the atomic picture, temperature is a measure of the average kinetic energy of the the molecules.
Therefore, an ideal gas is one in which the internal energy consists of only the kinetic energy of the atoms.
In particular the ideal gas law takes no account of potential energy due to molecule-molecule interactions
Now we'd like to relax this ideal and consider the very simplest way of taking into account interaction energies among the particles of a gas.
Molecular potentials
In a real gas of particles, there are attractive and repulsive forces between the particles. In what follows, we will *not* consider the possibility of breaking chemical (covalent) bonds. But there are still....
 Attractive
interactions can arise from at any of these
mechanisms:
Attractive
interactions can arise from at any of these
mechanisms:
- Forces between permanent dipoles and other permanent dipoles,
- Attractions between permanent dipoles and induced dipoles in non-polar molecules (pictured), and
- Attractions between mutually induced dipoles (London forces)
- Ions of opposite charge.
Induced dipoles work very much like rearrangement of charge in a wall that leads to the attractive interaction between statically charged balloons and walls!
In the picture, the molecule on the left is meant to represent water: oxygen has a higher electronegativity than hydrogen, so the oxygen side of the molecule has somewhat more negative charge than the hydrogen-bearing side. The molecule on the right is one that is isotropic in the absence of others, but if there is excess charge about, the electron cloud and nucleus will re-arrange a bit, causing an induced dipole.
Repulsive interactions include, most prominently the "hard-core" repulsion, which is a shorthand for "what keeps two atoms from fusing into one if their paths cross".
What does this consist of? Two atomic nuclei cannot easily overcome their electrostatic repulsion. But maybe when two atoms collide they could share electrons and the two nuclei could co-habit at a distance? Sure, this is precisely what happens in solids (but then they're no longer gases), or in covalent compounds (say, carbon dioxide). But for the covalent compounds, once you have filled shells for both atoms, you can't shove any more electrons into the already occupied orbitals (because of the Pauli exclusion principle). So it's not going to easily happen that two CO${}_2$ molecules will fuse.
The combination of the short-range repulsion and long-range attractive interaction is often modelled as a Lennard-Jones potential for particle-particle interactions. But for our purposes, we don't really care what the origins or even the distance-dependence of such an interaction is.
- Imagine that particles with a certain average kinetic energy (temperature) are infinitely far apart from each other.
- Now, imagine they are brought closer together and the particle-particle interactions start to be felt.
- The internal energy of the system is conserved, and consists of two pieces: a) kinetic energy of molecules ($\propto T$) and b) interaction energy.
- What happens to the temperature if there's an attractive interaction between the particles?
- if there's a repulsive interaction?
The van der Waals equation of state
$$\left(P+\frac{a}{v^2} \right)(v-b) = RT.$$ is identical to the ideal gas law equation of state, when $a\to 0$ and $b\to 0$. So, imagine that we have a van der Waals gas with $a=0$ and $b=0$, and have knobs that let us slowly turn up $a$ or $b$ parameter, while treating $P$ and $v$ as if they were constants. How would the temperature (kinetic energy) of such a gas change?
Treat $T=T(a,b)$ and write... $$dT = \left( \frac{\partial T}{\partial a} \right)_b da + \left( \frac{\partial T}{\partial b} \right)_a db.$$
Assuming that $a$ and $b$ are small numbers, we can expand the van der Waals equation of state, and write: $$RT= Pv -Pb + a/v -\frac{ab}{v^2} \approx Pv -Pb + a/v.$$
In the neighborhood of the ideal gas (small values of $a$ and $b$): $$ \frac{\partial T}{\partial a} = +1/v ; \frac{\partial T}{\partial b} = -P.$$
Evidently $a$ is some sort of attractive interaction term, and $b$ is a repulsive term.
This can also be seen by examining the expression for the critical temperature: $$T_c = \frac{8a}{27Rb}.$$
Two kinds of experiments highlight the character of ideal gases.
Gay-Lussac-Joule Experiment
How to design an experiment to measure, and see if it's really true that $$(\partial u/\partial v)_T=0?$$
Using the cyclical relations, we could write this... $$\left( \frac{\partial u}{\partial v} \right)_T = - \left( \frac{\partial u}{\partial T} \right)_v \left( \frac{\partial T}{\partial v} \right)_u=-c_v \left( \frac{\partial T}{\partial v} \right)_u.$$
So in order to test this, we need to make measurements at constant internal energy. How?
Since: $$du=\delta q - \delta w,$$ we need to study a change in a system which is thermally insulated ($\delta q=0$) from its surroundings, and also "mechanically insulated" (that is, fixed boundary so that no work is done).
 Our system comprises *both sides* of this container.
Our system comprises *both sides* of this container.
After the partition is punctured, the gas expands freely. Though this is clearly not an equilibrium process, the temperature and the internal energy only depend on the initial and final state (why?).
So... $$T_1 = T_0+\int_{v_0}^{v_1} \left(\frac{\partial T}{\partial v}\right)_u dv \equiv T_0+\int_{v_0}^{v_1} \eta dv.$$
The result of many attempts to measure the Joule coefficient $\eta$, are $$| \eta | < 0.001 {\rm \ K\ kilomole\ m}^{-3}.$$
[Carter's discussion of this depends on making an argument involving entropy, so I'll leave it for now...]
Joule-Thomson experiment
The claim is that, for an ideal gas, $h(T,P)=h(T)$, that is $\partial h/\partial P=0$.
As with the internal energy, using the cyclical relations, we could write... $$\left( \frac{\partial h}{\partial P} \right)_T = - \left( \frac{\partial h}{\partial T} \right)_P \left( \frac{\partial T}{\partial P} \right)_h=-c_p \left( \frac{\partial T}{\partial P} \right)_h.$$
So we need to measure at constant enthalpy.
In the Joule-Thomson apparatus,
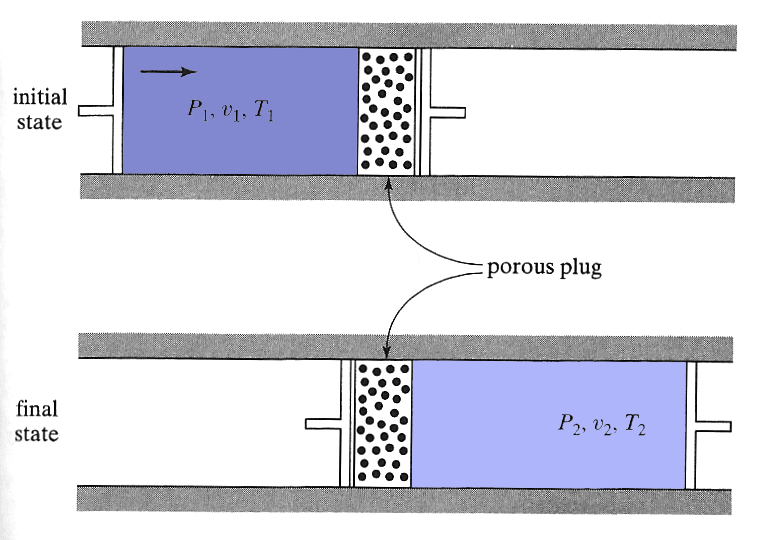
- two compartments are connected through a porous barrier.
- On the left, a pump keeps the pressure outside of the (~ frictionless) piston constant at $P_1$.
- On the right, a pump keeps the pressure outside the (~ frictionless) piston constant at a lower pressure $P_2$.
- Gradually (quasistatically) matter moves from the left chamber to the right.
- Both cylinders are insulated, So $T_1$, and $T_2$ are not changing. But perhaps $T_1 \neq T_2$. The goal of the experiment is to measure $T_2$.
- All the material starts on the left ($v_2=0$ initially), so the initial conditions of the chunk of gas are $P_1, T_1, u_1$, and the final conditions (when everything has been removed to the right) are $P_2, T_2, u_2$.
Since the system (consisting of both the left- and right-hand sides) is insulated from the surroundings, $\delta q = 0$. The first law saws, $$\delta q = 0 = du +dw.$$
Integrating... $$u_2 - u_1 = -\Delta w = -\left(\int_{v_1}^0 P_1\,dv + \int_0^{v_2} P_2\, dv \right)=-\left(-P_1v_1+P_2v_2\right).$$
Rearranging... $$u_2+P_2v_2=u_1+P_1v_1, $$
This says $h_2 = h_1$, that is, that this process is isenthalpic.
The temperature of the gas when everything has moved to the right is: $$T_2 = T_1 + \int_{P_1}^{P_2} \left( \frac{\partial T}{\partial P}\right)_h dP \equiv T_1 + \int_{P_1}^{P_2} \mu dP ,$$ where $\mu$ is called the Joule-Thompson coefficient.
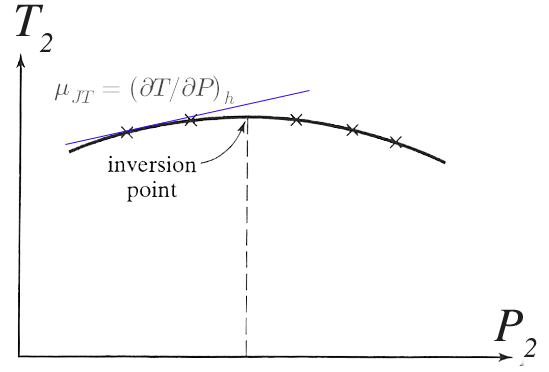 For many trials, all at the same $P_1, T_1$, but varying $P_2$, we map out the observed $T_2$, which looks like this...
Then, $\mu_{JT}(T_2)$ is the slope of the curve on a $T_2$ vs $P_2$ diagram at a particular temperature $T_2$. $\mu_{JT}$ should be zero for a truly ideal gas. What about approximately ideal actual gases?
For many trials, all at the same $P_1, T_1$, but varying $P_2$, we map out the observed $T_2$, which looks like this...
Then, $\mu_{JT}(T_2)$ is the slope of the curve on a $T_2$ vs $P_2$ diagram at a particular temperature $T_2$. $\mu_{JT}$ should be zero for a truly ideal gas. What about approximately ideal actual gases?
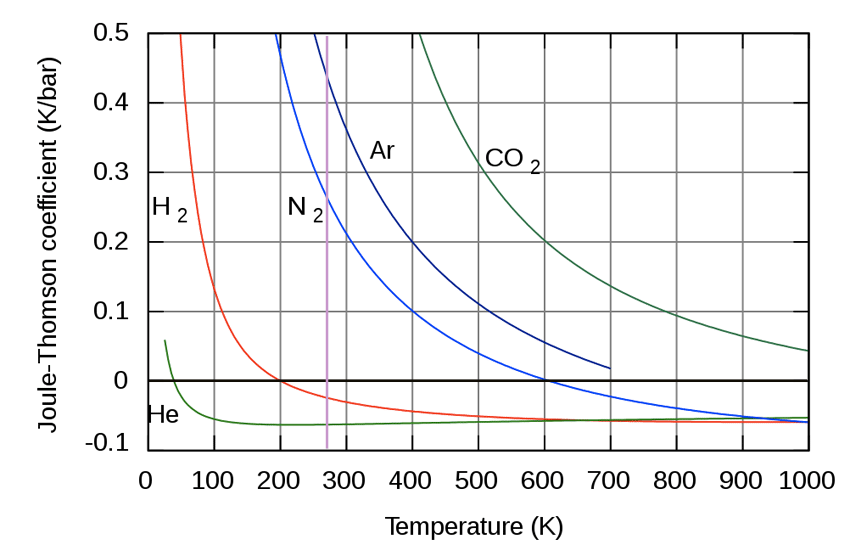
For most gases, at room temp, and at 1 atm, $\mu_{JT} > 0$, that is, the gases *cool* on expansion. The two notable exceptions are hydrogen and helium.
J-T coefficient of a non-ideal gas
To push the analysis a bit further, it turns out that if we have an explicit equation of state (we'll use van der Waals), we can calculate $\mu_{JT}$ if we use one result from thermodynamics that can be shown later, namely: $$\left(\frac{\partial h}{\partial P}\right)_T = v-T\left( \frac{\partial v}{\partial T}\right)_P.$$
[The calculations are shown in the class notes. But I'll skip ahead to the results of the calculation for a van der Waals gas...]
That original relation involving $\mu_{JT}=(\partial T/\partial P)_h$ was... $$\left( \frac{\partial h}{\partial P} \right)_T = -c_P \left( \frac{\partial T}{\partial P} \right)_h.$$
Subbing that new, magical relation in... $$v-T\left( \frac{\partial v}{\partial T}\right)P = -c_P\,\mu_{JT}.$$
Rearranging for $\mu_{JT}$, $$\mu_{JT} = \frac{T\left( \frac{\partial v}{\partial T}\right)_P -v}{c_P}.$$
Such that now we just need to come up with $(\partial v / \partial T)_P$ for the gas in question.
[Show that this vanishes for an ideal gas, by calculating $\left(\frac{\partial v}{\partial T}\right)_P$ from the ideal gas law, and subbing in to the numerator above...]
Expanding the van der Waals equation of state as before, $$Pv \approx RT +Pb-a/v.$$
Dividing by P... $$v =\frac{R}{P}T+b -\frac{a}{RT}.$$
So the partial derivative is... $$\left( \frac{\partial v}{\partial T} \right)_P =\frac{R}{P} +\frac{a}{RT^2}.$$
Using this, and the van der Waals approximation for $v$ to calculate that combination involving $T$ and $v$... $$\begin{align} T\left( \frac{\partial v}{\partial T}\right)_P -v & = \frac{RT}{P} +\frac{a}{RT}-\left(\frac{R}{P}T+b -\frac{a}{RT} \right) \\ & = \frac{2a}{RT}-b\end{align}$$
So, finally we can pull together this expression for $\mu_{JT}$ for a van der Waals gas:
$$\mu_{JT} = \frac{2a}{c_PRT}-\frac{b}{c_P}.$$
- At low temperatures, $\mu$ is positive, and depends only on $a$. $$\mu_{JT} \approx \frac{2a}{c_P\,RT},$$
- At high temperature, $\mu$ is negative and depends only on $b$., $$\mu_{JT} \approx -\frac{b}{c_P}.$$
The predominant interaction between atoms is the attractive one. It takes energy to pull the atoms apart, and that energy is extracted from the kinetic energy.
The predominant interaction between atoms is the (hard core) repulsion. As the atoms are separated, the potential energy is lowered and goes into increased kinetic energy.
Image credits