First Law of Thermodynamics
...an internal energy function, $U$, exists that is a state function.
That is, $dU$ is an exact differential.
- Both mechanical work and heat have units of energy,
- But neither one is path independent: It is usually the case that$$\oint \delta Q \neq 0,$$ and $$\oint \delta W \neq 0.$$
The hypothesis of energy conservation
- We suspect that there is a unique, total energy, $E$, for any system (that is to say, it's a state function),
- The total energy $E$ includes: kinetic energy of the center of mass ("traditional" or GPhys kinetic energy...), potential energy, internal energy ($U$), chemical energy, plus other forms of energy,
- When heat $\Delta Q$ is added to a system, or when the system performs work $\Delta W$, the total energy, $E$, of a system changes according to: $$dE = dE_{\rm pot} + dE_{\rm K.E.} +dU+dE_{\rm chem} +...= \delta Q - \delta W.$$
- It's possible to do work and/or transfer heat to a system with no changes in the non-$U$ forms of energy: K.E. of the CM, potential, chemical, etc. When this is the case, we say the internal energy changes according to: $$dU = \delta Q - \delta W.$$
Convention:
$\delta Q \gt 0$ means that heat energy flows in to the system,
$\delta W \gt 0$ is the work that a system does on its surroundings, so this is an energy flow out of the system.
We write the change in internal energy as an exact differential because this particular combination of inexact differentials is exact, that is $$\oint dU =\oint\left(\delta Q - \delta W\right) = 0.$$
Sort of like realizing: Depending on the day, I might run and/or walk to class, a distance of 300 m from my dorm room.
 The distance that I run can be 50 meters or 100 meters or nothing or something else.
The distance that I run can be 50 meters or 100 meters or nothing or something else.
- The distance that I walk might be 70 meters, or as much as 300 meters
But somehow when I add the walking and running distances together, it *always* equals 300 meters!
the_alien_experience
"Random" motion
 The "kinetic energy" of an object or container of atoms only depends on the speed of its center of mass,
$v_{\text{CM}} $. And yet we know that the atoms in the object/container are also in motion...
The "kinetic energy" of an object or container of atoms only depends on the speed of its center of mass,
$v_{\text{CM}} $. And yet we know that the atoms in the object/container are also in motion...
We shall see that for an ideal gas, $T\propto \text{KE}_\text{ave}$, the average energy of the atoms (not of the CM of the system...)
A portion of what we mean by "internal energy" is the kinetic energy of these atoms.
Play around with this molecular simulator to see their depiction of how heat or work on the system can cause the atoms to speed up.
For a monatomic gas, it is a pretty good approximation that *all* the internal energy is in the form of kinetic energy of each atom. And under these circumstances, $U\propto T$ alone. [See problem 3-7]
What other kinds of "internal energy" might there be besides the kinetic energy of the center of mass of atoms?
Equivalence of mechanical work and heat
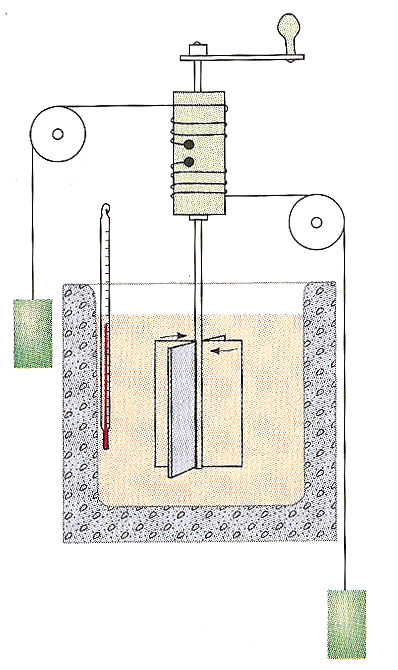 Joule's
experiment (right) measured the equivalence of mechanical work and heat. In
what sense?
Joule's
experiment (right) measured the equivalence of mechanical work and heat. In
what sense?
The system of water at right is insulated, so no heat can flow in ($\delta Q=0$). All the mechanical energy $\delta W_{\rm dis}$ is dissipated in the water. So the dissipative work must have gone towards changing the internal energy. $$dU = -\delta W_{\rm dis}.$$
On the other hand, the same change in internal energy could be brought about by isolating the system mechanically and only supplying heat. $$dU = \delta Q$$
So, with these restrictions, a certain quantity of dissipative work, or that same quantity of heat energy will always change the system in the same way.
Problem 3-8
A gas is contained in a cylinder fitted with a frictionless piston, and is taken from the state $a$ to the state $b$ along the path $acb$. In all, 80 J of heat flowed into the system, and the system did 30 J of work.
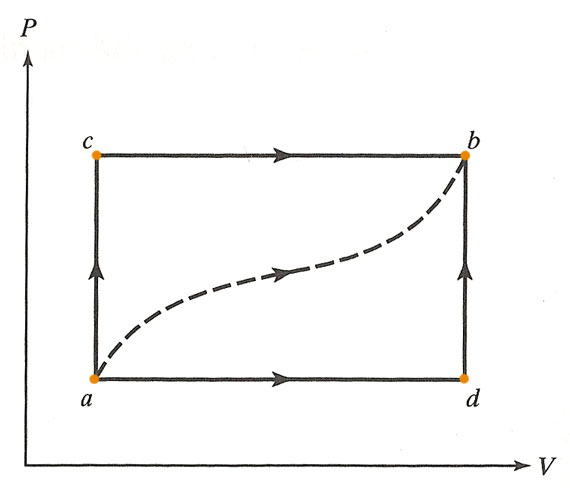
a.) How much heat flows into the system along $adb$ if the work done by the gas is 10 J?
Problem 3-7
Problem - Carter 3-7: Two kilomoles of a monatomic ideal gas are at a temperature of 300 K. The gas expands reversibly and isothermally to twice its original volume. Calculate (a) the work done by the gas; (b) the heat supplied. (For such an ideal gas, $U\propto T$ alone, so $\Delta U=0$ in an isothermal process).
I think I made a mistake by starting this problem in class in terms of specific volume, $v$. It seems like the total work should, in the end, depend on the quantity of material you have, $n$. So start as below... Assume that we are doing reversible work. Integrate $\Delta W =\int P(V)\,dV$
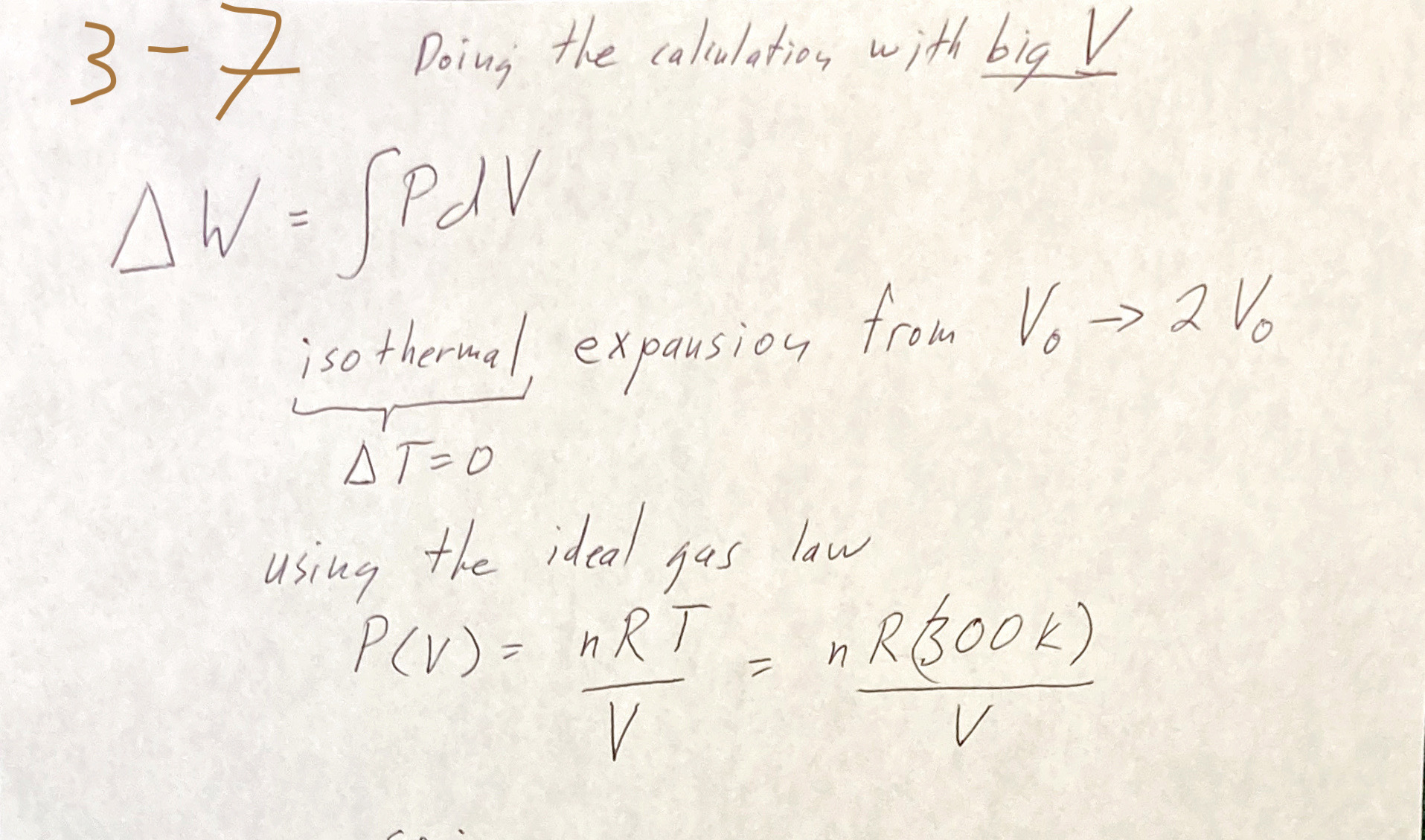
Adiabatic work is path independent
Normally, the amount of work to get from one state to another depends on the path taken.
But now imagine some adiabatically isolated system such that no heat can enter the system: It can only interact mechanically with its surroundings. Since $\delta Q=0$, the first law says for this particular case $$dU = -\delta W_{\rm ad}.$$
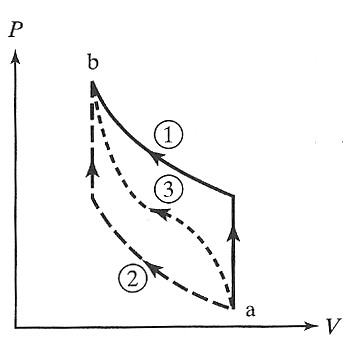 The work done by the system along one of the paths in the diagram shown is...
$$\int_{\mathcal P} \delta W_{\rm ad} = -\int_{\mathcal P} dU = -\Delta U.$$
The work done by the system along one of the paths in the diagram shown is...
$$\int_{\mathcal P} \delta W_{\rm ad} = -\int_{\mathcal P} dU = -\Delta U.$$
Since $U$ is a function of the thermodynamic state, it is path independent, so the adiabatic work for any process is path independent.
This also gives us a means of measuring changes in internal energy, by measuring the adiabatic work done.
Unfortunately, an adiabatic path does not necessarily exist between any two randomly chosen points.
When should work done on a system be considered work and when it should be considered heat? E.g. electrical work
- Depends on system definition.
- Work done ultimately boils down to being able to lift a weight.