Heat and Work
Changing the state of a system with heat and work.
Read Chapter 3 now.
Heat
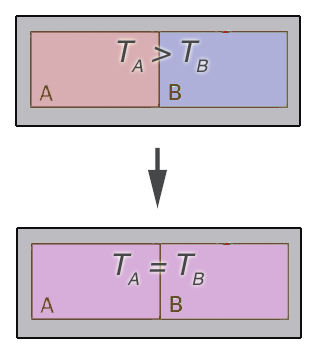 Consider two systems
which are initially at different temperatures, then they're brought
into contact...
Consider two systems
which are initially at different temperatures, then they're brought
into contact...
- Each system is enclosed by a fixed boundary.
- There's a diathermal boundary between the two systems.
- An adiabatic barrier around both isolates the two systems from the surroundings.
The state of both B and A change, and then eventually stop changing, at which point the two systems are in thermal equilibrium, and empirically it's found that they both have the same temperature.
No mechanical work has been done on either system (fixed boundaries)!
We say heat transferred from one system to the other is responsible for altering the system states.
Heat is energy transferred due to temperature differences only.
Phase transitions
 But "altering the system state" can also happen without a change in temperature, and without work being done on the system: During a phase transition, as water is boiled to steam, the temperature of the water is a constant 100 C. So, Carter suggests this more general definition:
But "altering the system state" can also happen without a change in temperature, and without work being done on the system: During a phase transition, as water is boiled to steam, the temperature of the water is a constant 100 C. So, Carter suggests this more general definition:
Heat is the change in internal energy of a system when no work is done on or by the system.
Units (of energy)
 1 kilocalorie = heat energy needed to raise the temperature of 1 kg of water from 14.5 C to 15.5 C = 1 Calorie.
1 kilocalorie = heat energy needed to raise the temperature of 1 kg of water from 14.5 C to 15.5 C = 1 Calorie.
Also
1 calorie = heat energy to raise 1 cc of water from 14.5 to 15.5 C
Human power
Power is Energy / time: a rate of energy consumption/generation:
1 Joule / second = 1 Watt.
 An average human diet (USA) of 2000 Calories / day works out to what average power (in Watts)?
An average human diet (USA) of 2000 Calories / day works out to what average power (in Watts)?
1 Joule = 1 kg m / sec${}^2 = 2.39 \times 10^{-4}$ kcal
So 2000 Calories/1 day=2000 kcal/day:
$$\frac{2000 \text{ Cal}}{\text{1 day}}
\frac{1 \text{ J}}{2.39\times 10^{-4} \text{ Cal}}
\frac{1\text{ day}}{24\cdot 3600 s}
=96.9\text{ J/s}$$
About 100 Watts
 Elite cyclists can put out ~400 Watts (or 500 W total) over the course of a Tour de France stage, and bursts of 2000 Watts for a few seconds.
Elite cyclists can put out ~400 Watts (or 500 W total) over the course of a Tour de France stage, and bursts of 2000 Watts for a few seconds.
Changing the state with both heat and work
When we look at more complicated processes that involve both tranferring heat to a system and performing work on it, we find...
- The amount of heat needed to go from one state to another depends on the path.
- $\Rightarrow$ We'll write a small heat transfer as $\delta q$.
- $\Rightarrow$ Bodies don't contain a fixed amount of heat. Heat is only identified as it comes across a system boundary.
Adiabatic processes are changes of state where no heat is transferred.
 With sudden changes, we will make the assumption that if things happen "fast enough", there is no time for heat to flow into a system (e.g hammer + board) from the surroundings.
With sudden changes, we will make the assumption that if things happen "fast enough", there is no time for heat to flow into a system (e.g hammer + board) from the surroundings.
Work
The other means of changing the system state apart from temperature differences is work. Many different kinds are possible:
- pressure and volume, $P\ dV$,
- surface tension and area, $\Gamma\ dA$,
- charge and emf, $q\ d{\mathcal E}$,
- Notice: each of these is the product of one intensive and one extensive quantity.
$\delta W > 0$ when the system does work on the surroundings.
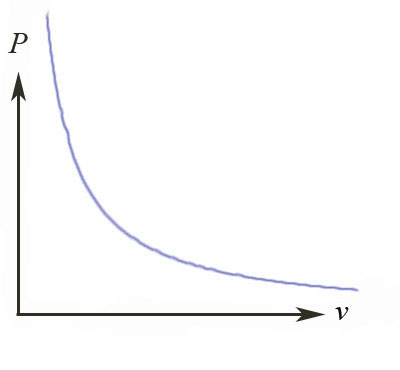
Isothermal process, ideal gas
- an ideal gas in a piston,
- with a heat bath keeping the temperature constant (isothermal process),
$$\Rightarrow P(v) = \frac{RT}{v},$$ so the net work performed by the system as it expands from $v_0$ to $v$ is:
$$\Delta W = \int \delta W = \int P\ dv = \int_{v_0}^v \frac{RT}{v'} \ dv' = RT\, \left. \ln(v')\right|_{v_0}^{v} = RT \, \ln\left( \frac{v}{v_0} \right).$$
- $\Delta W \gt 0\Rightarrow$ the system did work on its surroundings.
- $\Delta W \lt 0\Rightarrow$ the surroundings did work on the system.
Reversibility
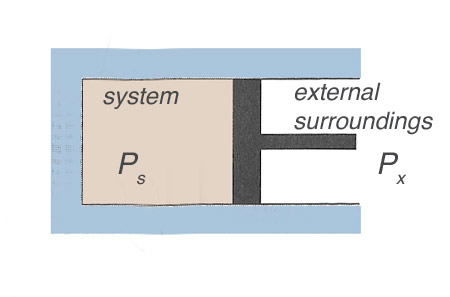
Consider a compressible, ideal gas in a piston.
The work done by the system is $\int P_s \ dV$.
The work done on the surroundings is $\int P_x \ dV$.
In general $P_x \neq P_s$.
In an extreme case, consider instead of a piston that we have a fixed wall, and outside a vacuum ($P_x = 0$). If we suddenly puncture the wall, no work is done on the surroundings.
Very generally, $$P_s = P_x \pm \Delta P.$$

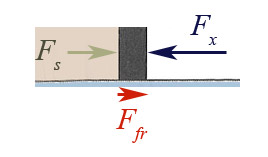
This difference in pressure, $\Delta P$, might arise because of friction,
which is always pointed opposite the direction of motion, whether moving to
the left or the right.
Even if there is no friction in the system, if the piston (mass $m_p$) is accelerated, the forces (and therefore the pressures) cannot be equal since $$a = \frac{| F_x - F_s|}{m_p}.$$
$\Rightarrow \Delta P=0$ only for frictionless, slow (quasistatic) processes.
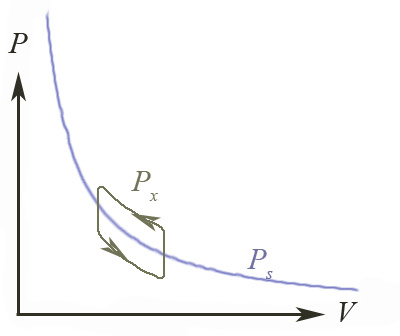 When
$\Delta P \neq 0$, the area inside the trace of $P_x$ represents the
energy dissipated
in one cycle of expansion and compression. This violates our condition of no
dissipation for a reversible process.
When
$\Delta P \neq 0$, the area inside the trace of $P_x$ represents the
energy dissipated
in one cycle of expansion and compression. This violates our condition of no
dissipation for a reversible process.
A reversible, cyclic process is one in which:
- No energy is dissipated.
- The system and the surroundings return to their initial state at the end of the cycle.
For any segment of such a cycle,
- the work done by the system is equal to the work done on the surroundings.
- An infinitesimal $\Delta P$ is all that is needed to reverse the direction of the process at any point.
Dissipitative and configuration work
If you pull a lever on a black box system, is the work that you do, $\delta W_0$, "recoverable" or not?
| Configuration work | Dissipitative work |
|---|---|
 |
 |
Behavior under time reversal |
|
| $$\delta W_{\rm tr} = -\delta W_0$$ | $$\delta W_{\rm tr} = +\delta W_0$$ |
Show that $I^2R$, and friction forces are the same in either direction.
Image credits
Flickr users Cayusa, Kevin Saff, Diana Schnut, Alice Daer