Equations of state
In which we consider two equations of state:
- The ideal gas law, $Pv=RT$.
-
 The van der Waals equation of state.
The van der Waals equation of state.
Extensive and intensive variables
Consider one thermodynamic system at equilibrium at a particuler $P$, $V$,
and $T$, and then divide it in half...

The volume $V$ of each subsequent half-system is half of its original value. $\Rightarrow V$ is an "extensive" parameter.
But the pressure and temperature of each half-system is the same as the original. $\Rightarrow P$ and $T$ are "intensive" variables.
"Specific" variables
- You can convert an extensive variable to an intensive one by dividing by the quantity of material $n$ (number of kilomoles).
- You prepend the word "specific" onto such quantities, indicating that they are "per (kilo)mole".
Specific volume: $$v = V/n = \text{volume per kilomole}.$$
Ideally, we would like to write all extensive quantities in upper-case, e.g. $V$ and...
all intensive variables in lower-case.
Unfortunately, temperature as $t$ looks too much like time, and pressure as $p$ looks too much like momentum. So, we'll continue to use $P$ and $T$ (even though they're intensive).
Equations of state
The central assumption of thermodynamics is that there is a simple state function: $$f(P, V, T, .... ) = 0$$ ...which defines a surface in state space.
The most familiar equation of state that relates $P$, $V$, and $T$ is the...
Ideal gas law
Over a century or so, laws relating $P$, $V$, and $T$ where put forth by.. Avogadro, Boyle, Charles, Gay-Lussac.
In 1834 Emile Clapeyron synthesized these together as... $$PV = nRT,$$
where...
- $P$ - pressure in Pa,
- $V$ - volume in ${\text m}^3$,
- $n$ - quantity of matter in kilomoles,
- $T$ - absolute temperature in degrees K,
Then, the gas constant $ 8.314472 \times 10^3 {\rm J} \cdot {\rm K}^{−1}\cdot {\rm kmol}^{−1}$. (* warning chemists...)
Or, using $n=m/M$ where
- $m$ - mass in kilograms,
- $M$ - molecular weight: *kg per kmol. E.g. for Carbon: $M =$ 12.0107 grams / mole = 12.0107 kg / kilomole.
Here is the ideal gas law in terms of intensive variables only: $$Pv=RT.$$
How ideal?
The ideal gas law will eventually be shown to be an exact result for an idealized gas made up of...
- point particles: volume of each particle $\to 0$),
- noninteracting: interparticle force $\to 0$.,
So it's a good approximation for real gases...
- at low pressures (relatively small volume per particle), and...
- at high temperatures (attractive forces negligible compared to impact forces),
- or for noble gases (smaller attractive forces).
Ideal gas diagrams
You can examine the equation of state and plot one variable as a function of another while holding the third constant. That way of thinking of the equation of state leads us to consider
Isochore plots
Solve the ideal gas law for $P(v,T)$. Now hold the volume constant (isochore) and plot $\left(P(t)\right)_v$ .. $$P = \left( \frac{R}{v} \right) T \propto T.$$
- $0.7 v_0$
- $v_0$
- $1.2 v_0$
Isobar plots
Solve the ideal gas law for $v$. Now hold the pressure constant (isobar) and sketch $v(T)$...
$$v = \left( \frac{R}{P} \right)T \propto T.$$
- $0.7 P_0$
- $P_0$
- $1.2 P_0$
Isotherm plots
Solve the ideal gas law for pressure $P$. Now holding the temperature constant (isotherm) and plot $P(v)$...
$$P = \left(RT\right) \frac{1}{v} \propto \frac{1}{v}.$$
- $1.2 T_0$
- $T_0$
- $0.7 T_0$
State-space surfaces
Here, we've written the temperature $T(P,v)$ as a function of pressure and volume, namely $$T(P,v)=\frac{Pv}{R}.$$
Using, GeoGebra, we can picture the state surface (a 2-dimensional
surface embedded in 3-dimensions) directly.
In this visualization, I'm graphing in units such that $T=P*v$ using the $x$ axis for $v$; the $y$ axis for $P$, and the $z$ axis for $T$.
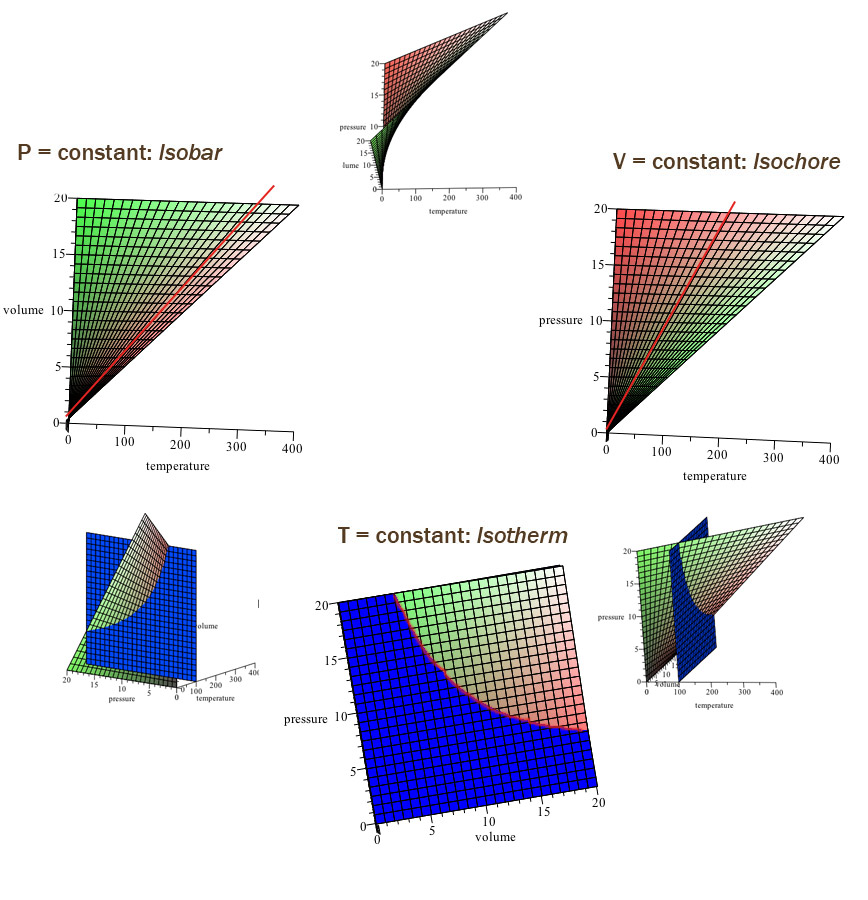
What features of real materials does the ideal gas law fail to capture??
Van der Waals
The van der Waals equation of state results in a phase transition as temperature drops... $$(P+a/v^2)(v-b) = RT.$$
What is the limit of this equation as $a\to 0$ and $b\to 0$??
Now we're going to plot several isotherms of the VdW equation. That, we'll hold $T$ constant and plot $P$ vs $v$. Notice that we're using $v$ (intensive) not $V$ (extensive).
What is the normal behavior of a gas? As you compress a quantity of gas (higher density = lower $v$) what does the pressure do?? What does this imply about the slope $\del P/\del v$? What does this imply about the work you must do on the gas--positive or minus--to compress it?
Solving for $P$, $$P=\frac{RT}{v-b}-\frac{a}{v^2}.$$
In the figure below, we hold $T$ constant, and then graph $P$ vs $v$.
Then we lower the (constant) $T$, and graph $P$ vs $v$ again, then repeat.
Below a certain critical temperature (in purple) an unstable region
appears, and phase separation occurs.
Parameters: a=20 b=1 => v_c=3b=3 T_c = 8a / 27Rb => RT_c = 160/27 p_c = a / 27b^2 = 20/27
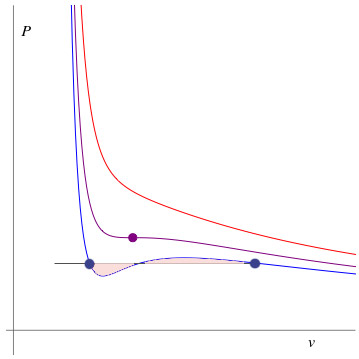
- $T \gt T_c$
- $T_c$
- $T \lt T_c$
The critical temperature, $T_C$, is observed as you cool the system down when a single point with slope=0 appears on the $P-v$ plot: $$\left.\left(\frac{\partial P}{\partial v}\right)\right|^{T=T_C} = 0 = -\frac{RT}{(v-b)^2}+\frac{2a}{v^3},$$
- Is there an inflection point (zero curvature) on the curve at (and below $T_C$? Why?
There is certainly an inflection point *somewhere* on that curve, since it is concave up towards the left and concave down towards the right....
- Is it possible that the inflection point is different from that point of zero slope?
No. There would have to be more than one place where the slope was zero.
Inflection point: $$\left(\frac{\partial^2 P}{\partial v^2}\right) = 0 = \frac{2RT}{(v-b)^3}+\frac{6a}{v^4},$$
We should like to find $T_C$, $P_C$, and $v_C$ at that critical point. Do we have enough constraints? Are there other unknowns?
Cooling a system with $v_c$ to a temperature below $T_c$ in a container with a fixed volume.
- According to the graph, what would the slope $\del P/\del v$ be for a phase with the density $v_c$ when $T$ is below the critical temperature $T_c$?? What would this imply about the stability of the system?
Most substances resist when you push on them. That is, if you would like to increase their density (=reduce their $v$) you must supply a higher pressure...
$\Rightarrow \frac{\del P}{\del v}\lt 0$. This is true of the v.d.W. gas above the critical temperature.
But at $v_c$ for $T \lt T_c$ the v.d.W. gas has $ \frac{\del P}{\del v}\gt 0$. If the density goes up, $v$ goes down and the $P$ goes down .If you let off the pressure, the system's density will go up, a fancy way of saying "it will collapse". Such a substance is said to be "mechanically unstable". It will not stay in such a state.
- How would such an unstable system change?
It collapses to a higher density$\equiv$ lower $v$.
- Let's say $v$ changes from $v_C$ if the phase becomes "mechanically unstable". How does $v$ change? Does the substance still occupy the whole container volume?
- phase separation is the idea that some of the material exists at one $v=v_A$ and another portion exists at a different molecular volume, $v_B$. How would this get you out of the quandary above?
some of the material has to exist at a higher volume (per molecule) so that the total volume stays the same.-->
- If you had two phases in the same container,
What thermodynamic variable(s) must be the same for each portion if they are in equilibrium, both mechanical and thermal equilibrium?
Think of the two-phase system as consisting of two subsystems each consisting of just one phase, with no wall between them.For the two subsystems to both be in equilibrium they must have the same temperature (thermal equilibrium) and since there is no rigid wall separating the phases, they must have the same pressure (mechanical equilibrium).
but those two sub-systems have to be in equilibrium with each other, so had better have the same pressure--->