Fermions and Bosons
Actually, electrons (one kind of fermion) are seriously indistinguishable from each other. (Ditto for bosons all of the same type).
Therefore, the state in which "electron #1" is in energy level 3 is indistinguishable from the state in which "electron #2" is in energy level 3 because there is no experiment that we can do to distinguish 1 electron from another. This will affect how we count the number of microstates!
But we shall see that there is a limit in which these QM particles still behave "as if" they were distinguishable.
Learning how to count again...
Carter uses the metaphor of shelves (shelf $j$ has energy $E_j$) which contain many (degeneracy $g_j$) bowls (quantum states). Let's consider dropping a certain number ($N_j$ particles) of M&Ms among the bowls on shelf $j$...
Particles within one energy level
Boltzmann statistics
The M&Ms are each different--distinguishable. One is red, one is a Peanut M&M, Another green regular one is missing part of the first M... There is no restriction in how many we can put in one bowl.
We can put the first particle in any one of the $g_j$ bowls. We can put the second particle in any one of the $g_j$ bowls. ....
How many possible arrangements for $N_j$ particles and $g_j$ bowls?
The answer is: $$g_j*g_j....*g_j=g_j^{N_j}$$
How many ways are there of arranging 2 distinguishable particles in 4 quantum states?
Fermi-Dirac statistics
Fermions - particles with spin $s=1/2 + n$.
Most prominent example: the electron has a total angular momentum quantum number of 1/2. The $z$-component of its spin is only ever measured to be +1/2$\hbar$ or -1/2$\hbar$.
The Pauli exclusion principle says, that taking into account spin,
No two fermions can be in the same quantum state.
Furthermore, all fermions are indistinguishable
How many ways of distributing $N_j$ fermions among $g_j$ quantum states?
Think of each bowl as either having an electron in it, or not. Then, we can ask, How many sequences of length $g_j$ are there that have $N_j$ Filled (Heads) and $g_j-N_j$ Empty (Tails) bowls (coins) in them?
The answer is $$\frac{g_j!}{N_j!(g_j-N_j)!}= {g_j \choose N_j}.$$
How many ways are there of arranging 2 identical fermions in 4 quantum states?
Bose Einstein statistics
Bosons - particles with spin $s= n$.
Most prominent example: the photon is a spin 1 particle.
Unlike fermions, any number of bosons can occupy the same quantum state. However, they are indistinguishable from each other.
How many ways of arranging $N_j$ bosons among $g_j$ states?
There is an elegant way of calculating this, that once again maps onto the coin-counting problem: Represent the *boundaries* between the degenerate states (bowls) as sticks, and the particles as circles. The picture below depicts one arrangement of
- 9 particles distributed among
- 8 bowls, denoted with 7 stick boundaries
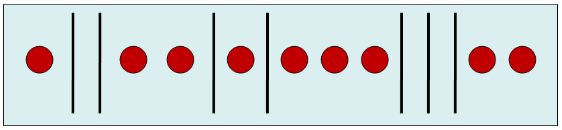The number of particles is $N_j$, the number os states is $g_j$. But the number of sticks is $g_j-1$. We should like to figure out the number of ways of arranging $N_j$ particles (Heads) and $g_j-1$ sticks (Tails). How many is that?
The answer is: $$\frac{(N_j+g_j-1)!}{N_j!(g_j-1)!}$$
How many ways are there of arranging 2 identical bosons in 4 quantum states?
Examples
For a gas of a) Distinguishable particles, b) fermions, c) bosons:
In a system with two microstates, and two particles, what is the probability that you will find one particle in each microstate?
(Problem 13-2) Five particles occupy the $k$th energy level, which is ten-fold degenerate. How many possible microstates are there?
See the diagram on page 253 for a comparison of the distributions:
Fermions / Bosons / Dilute gases
Important modifications for our scheme: quantum particles are empirically indistinguishable, so we need to modify our counting rules. $$\Rightarrow f(E)=\frac{1}{e^{(E-\mu)/kT}+1}.$$
Fermi-Dirac distribution.
Bosons - particles with spin $s=n$.
Any number of bosons can be in a particular quantum state. $$\Rightarrow f(E)=\frac{1}{e^{(E-\mu)/kT}-1}.$$
Bose-Enstein distribution.
Dilute gas - distinguishable particles, but assuming occupation numbers are typically small, $N_j << g_j$. In this limit, it shouldn't matter whether a particle is a fermion, or a boson, or a classical, distinguishable particle. $$\Rightarrow f_j=\frac{N_j}{g_j}=\frac{Ne^{E_j/kT}}{Z}.$$
The Maxwell-Boltzmann distribution.