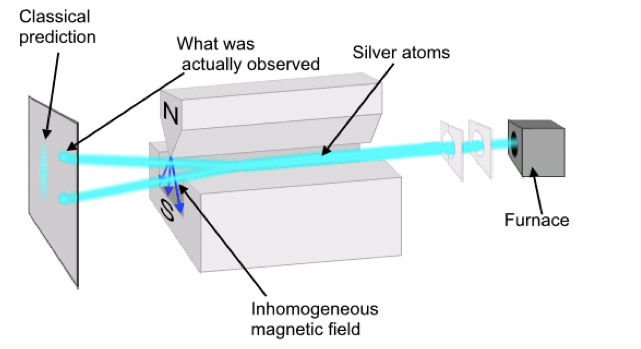
Binary systems
A quantum spin-1/2 particle has two allowed states (in a magnetic field) that we'll call up or down.
A spin system with several spins on a lattice. Each spin can be oriented
either up or down:
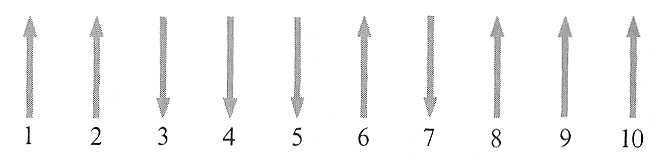
This particular configuration has a probability of $1/2^{10}$.
But could just as easily be a parking lot with cars present (or not):

Or a set of 10 coins.
The *spins* (or magnets) each has magnetic moment $m$. We'll assume the spins
do *not* interact with each other, but only with an external field.
Coins $\rightarrow$ spins
There is an exact analog of coins to spins in spin -1/2 systems: A system made up of atoms with one unpaired electron. In each atom, the spin can either point up or down (with reference to a magnetic field that will eventually be turned on.) Let $N_H\rightarrow N_\uparrow$ and $N_T\rightarrow N_\downarrow$. As with coins... $$N_\uparrow + N_\downarrow=N.$$
If we select units such that the spin on one particle is +1 or -1, then the spin excess $2s$ (assuming $N$ is even) is: $$N_\uparrow - N_\downarrow = 2s,$$ where $s$ is an integer.
If the magnetic moment per spin is $m$, then the net magnetic moment of the system is $2sm$.
The number of ways of arranging the $N$ spins to have a spin excess of $2s$ is $$w(N,s)=\frac{N!}{(N/2 + s)!(N/2-s)!}=\frac{N!}{N\uparrow!\,N\downarrow!}={N_\uparrow \choose N}.$$
$w$ is sometimes called the multiplicity function.
And the total number of microstates is $2^N=\Omega$
Sharpness of $w$
We can explore the properties of $w(N,s)$ using
Stirling's approximation, if we look at the logarithm of the distribution:
$$\begin{align}\ln (w(N,s)) = & \ln \left(\frac{N!}{(N/2 + s)!(N/2-s)!}\right)
\\
= & \ln N! - \ln[(N/2 + s)!] - \ln[(N/2-s)!] = \\
= & N\ln N-N\\
& -((N/2 + s)\ln (N/2 + s)-(N/2 + s))\\
&
- ((N/2 - s)\ln (N/2 - s)-(N/2
- s))\\
= &N\ln N-(N/2 + s)\ln (N/2 + s) - (N/2 - s)\ln (N/2 - s)\end{align}.$$
This can be graphed by fixing $N$, and allowing $s$ to vary. Or it can re-written slightly more compactly by writing $N\ln N=(N/2+s)\ln N +(N/2-s)\ln N$. Then... $$\ln(w(N,s)) = -(N/2 + s)\ln \frac{1}{2}(1 + 2s/N) - (N/2 - s)\ln \frac{1}{2}(1-2s/N).$$
See the Plots in 12.3.nb.
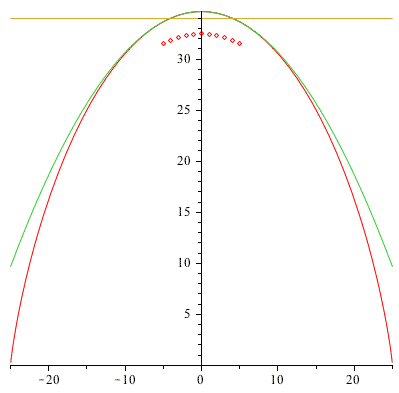
Kittel and Croemer (Thermal Physics, 1980) show that: $$\ln(w(N,s)) \approx \ln(w(N,0))-2s^2/N.$$ That is, near the maximum, the log of $w$ is approximately a quadratic function of $s$.
The graph shows the Stirling approximation, and the quadratic approximation
for $N=10$.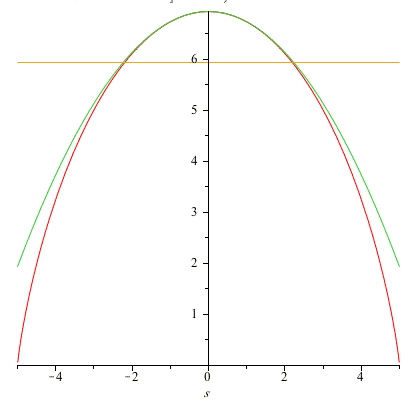
Taking $e^{(...)}$ of both sides of the quadratic approximation, we get...
$$w(N,s) = w(N,0) e^{-2s^2/N}.$$
This is a Gaussian distribution.
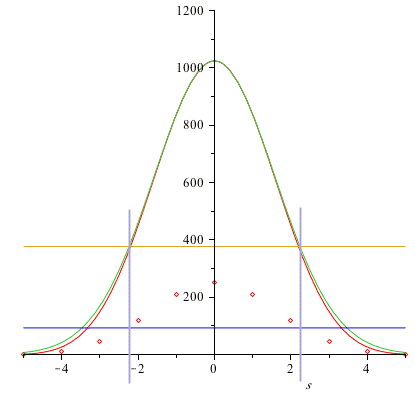 The
maximum value of the function occurs at $s=0$, and it drops to $e^{-1}=1/2.718$
of its maximum value at $s= \pm \sqrt{N/2}$.
The
maximum value of the function occurs at $s=0$, and it drops to $e^{-1}=1/2.718$
of its maximum value at $s= \pm \sqrt{N/2}$.
Or, recognizing $\Delta = s/N$ as a measure of the fractional width of the function.... $$\Delta = \frac{s}{N} = \frac{\sqrt{N/2}}{N}\propto \sqrt{\frac{1}{N}}.$$
That is, the function becomes fractionally sharper as $N$ gets larger.
 $N=50$
$N=50$
General observations with a large number of spins:
- The most probable macrostate is the one with the highest number $w(N,s)$ of microstates.
- The most probable macrostate becomes ever more sharply defined as the number of spins increases.
- It becomes overwhelmingly more likely to find the system in the most probable macrostate,
- So, this is effectively the equilibrium state.
Find the equilibrium state from $w(N,s)$
We could find the most probable macrostate by looking for $s$ such that $dw(N,s)/ds=0$.
Wherever $w$ has zero slope, $\ln(w)$ does too, so it would be just as good to look for $w_{max}$ by means of: $$\frac{d \ln(w)}{ds}=0.$$
In general, we need to find some place where the derivative vanishes, perhaps with regard to several occupation numbers.
Spin expectation value
The average value of the spin (with no magnetic field) is: $$\overline{s} = \sum_{s= -N/2}^{s=+N/2} s\,P(N,s)= \frac{\sum s\, w(N,s)}{\Omega}.$$
- $w(N,s)$ is a highly-peaked function, which is symmetric about $s=0$: $w(N,s)=w(N,-s)$.
- $s$ is a function that is anti-symmetric about $s=0$: $(-s) = -(s)$.
So the symmetric sum above is 0, $$\overline{s} = 0.$$
Fluctuations
The size of spin 'fluctuations' is given by (homework: 11.1.d) $$\sigma = \sqrt{\overline{s^2} - (\overline{s})^2}.$$
We know $\overline{s}=0$. It remains to calculate $\overline{s^2}=\int s^2 w(N,s) \,ds/\Omega$, which turns out to be $N/4$.
Energy of a system of spins
Consider a spin lattice: perhaps unpaired electrons of atoms in a solid. The spins are not free to move, so there's no kinetic energy, only potential energy, when a field is present.
When a magnetic field $\myv{B}$ is turned on, the potential energy of one magnetic moment $\myv m$ in the field is $$U= -\myv{m}\cdot \myv{B}.$$
And, for our $N$ spins, $$U=\sum{U_i} = -\myv{B}\cdot \sum \myv{m}_i = -2smB.$$
$U$ depends on the total spin excess, so we could write $U=U(s)$. When one spin is flipped, $2s$ changes by 1. The energy changes by integer amounts of $2mB$: $$U(s)-U(s+1)=2mB.$$
links: Finkelstein