Exact and inexact differentials
Thinking about distance
Consider the subtle difference between two kinds of distances:
- $D\equiv$ 'distance travelled': The distance from Goshen to Elkhart is 11 miles. So, if I travel from Goshen to Elkhart and back again along the shortest path, $\Delta D=22$ miles at the end of my trip.
- $R\equiv$ 'distance away' from Goshen: If I travel from Goshen to Elkhart and back again, $\Delta R=0$ at the end of my trip.
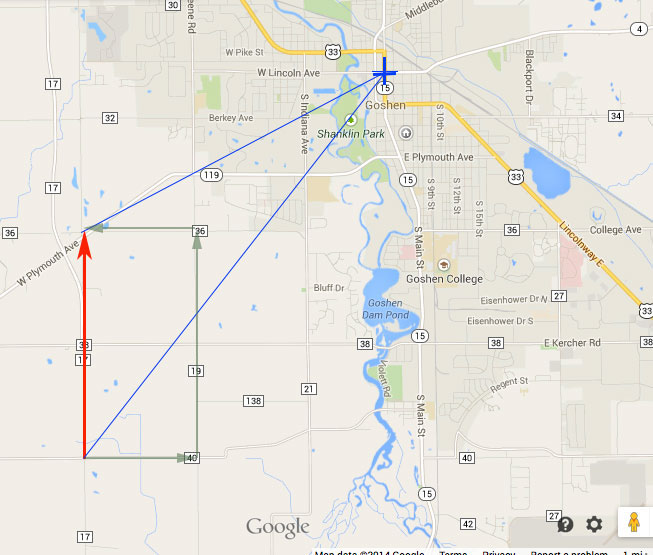
To do: The county roads in Elkhart County are laid out on a 1 X 1 mile grid. All the E-W roads have even numbers; All the N-S roads have odd numbers. Joe travels the red route along old CR 17, from CR 40 to CR 36. Estimate:
- The number of miles that Joe travels, $\Delta D$.
- The change in Joe's "distance away" from Goshen, $\Delta R$.
Next Joe travels the green/gray route. Again estimate
1. $\Delta D \ \ \ $ 2. $\Delta R$
Propose a scheme for using $R$ (distance away from the center of Goshen) as one coordinate to uniquely locate your position in Elkhart County.
Propose a scheme for using $D$ (distance travelled from the center of Goshen) as one coordinate to uniquely locate your position in Elkhart County.
Distances and differentials of distance
Both of these changes in distance could be evaluated by integrating small changes along a path ${\cal P}$:
- $\Delta D=\int_{\cal P}\delta D$ apparently depends on the path ${\cal P}$ (or 'history') travelled.
- $D$ was not very useful as a coordinate on a map.
- $\Rightarrow $ We say that $\delta D$ is an inexact differential and denote that by writing with the $\delta$ symbol.
On the other hand...
- $\Delta R = \int_{\cal P} dR$ is also found by integrating along a particular path,
- But the total change in "distance from Goshen", $\Delta R$ is the same for any path between two given points.
- $R$ could be used as part of a coordinate system to locate you on a map.
- $\Rightarrow dR$ is an exact differential and we write it with a '$d$' symbol in front of $R$ to indicate that.
What is $\Delta R=\int_{\cal P}dR$ for a path, $\cal P$, that ends at the same point where it started?
Is work exact or inexact?
We have an expression for the work done by a system (on its surroundings) at pressure $P$ when its volume changes by $dV$: $$\delta W \stackrel{?}{=} P\,dV;\ \ \ dW\stackrel{?}{=}P\,dV$$
If work has an exact differential, then integrating $P\,dV$ around any path in $P$, $V$ space should be 0. Try this path:

We found: $$\oint \delta W = \oint P\,dV =0 + \int_{V_1}^{V_2} P_2\,dV+0+\int_{V_2}^{V_1} P_1\,dV = (P_2-P_1)(V_2-V_1).$$ This is clearly not vanishing, so it must be $P\,dV=\color{blue}{\delta}W$ (not $\color{red}{d}W$).
Combinations of differentials
Let's say that you keep track of the miles you run, and the miles that you walk along a line--say for example, always staying on CR 40--like this:
- $x_r \equiv$ 'miles run north along CR 40',
- $x_w\equiv$ 'miles walked north along CR 40'.
To do: A 'journey' might consist of any mix of walking and running.
- How might you argue that the differential of $x_w$ is exact or inexact? (Consider a variety of journeys...)
- Is there any algebraic combination of differentials for walking and running that is exact?
Conclusion
At least sometimes it is possible to make an exact differential out of a combination of inexact differentials.
Is a sum of exact differentials exact or inexact? What about a product or a difference?