Thermodynamics

...is rooted in the study of heat in physics. But other big ideas coming out of it include...
- energy,
- entropy,
- statistical mechanics,
- information theory,
- 'systems' theories...
A theory is more impressive the greater the simplicity of its premises is, the more different kinds of things it relates, and the more extended its area of applicability. Therefore the deep impression which classical thermodynamics made upon me. It is the only physical theory of universal content concerning which I am convinced that, within the framework of the applicabilty of its basic concepts, it will never be overthrown.-Albert Einstein
The 'impressive theory' has it roots in very practical, engineering considerations...
The industrial revolution
Throughout most of our history the main sources of energy at our disposal were human and animal

But starting in 17th century Britain, there was a technological explosion. Machines which used the heat from burning coal powered trains, eventually factories, driving the transition from cottage industry, to something we recognize as more modern 'industry'.
Newcomen's engine - Narrated: 3 min.
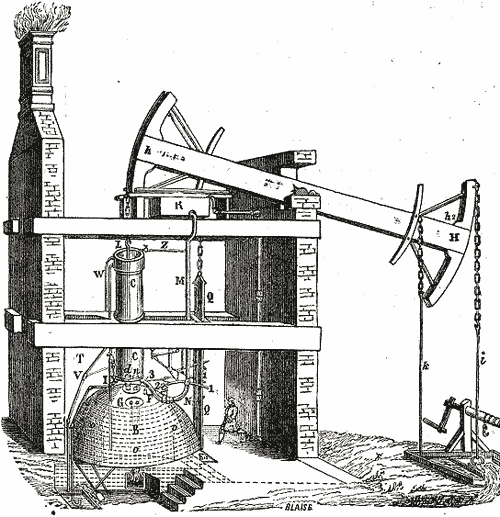 1712 - One of the first practical engines was Thomas Newcomen's which was used to
draw water up from coal mines.
1712 - One of the first practical engines was Thomas Newcomen's which was used to
draw water up from coal mines.
- A coal fire heats water to boiling.
- Steam fills the cylinder, displacing air.
- Steam valve closes.
- Cold water sprayed onto the cylinder causes the steam vapor to condense to water, creating a vacuum in the cylinder.
- Vacuum pulls piston & left side of beam down.
- Right side of beam pulls up weight attached below-ground.
The net effect: Thermal energy (heat) from burning coal was converted into mechanical energy.
Carnot
 1824 - Réflexions sur la Puissance Motrice du Feu ("Reflections
on the motive power of fire"), Sadi
Carnot came up with an abstract way of thinking about the steam engines
of his time--as a heat engine:
1824 - Réflexions sur la Puissance Motrice du Feu ("Reflections
on the motive power of fire"), Sadi
Carnot came up with an abstract way of thinking about the steam engines
of his time--as a heat engine:
Any machine which converts heat (generated by burning coal, gas, oil; or a nuclear chain reaction; ...) into mechanical energy.
He asked:
- Is the work available from a heat source potentially unbounded? or is there a limit?
- Can heat engines be improved by replacing the steam with some other "working fluid" or gas?
His theory was based on the idea of "caloric" of the time:
 Heat (what we *now* call it) was pictured as a material substance called caloric.
Heat (what we *now* call it) was pictured as a material substance called caloric.
 Like water falling over a water wheel, caloric "falls" from high temperature to lower temperature.
Like water falling over a water wheel, caloric "falls" from high temperature to lower temperature.
 Carnot concluded that the greater the
temperature difference in a heat engine, the more mechanical work could be done.
Carnot concluded that the greater the
temperature difference in a heat engine, the more mechanical work could be done.
 He thought (initially) that the total amount of caloric in a body was conserved.
He thought (initially) that the total amount of caloric in a body was conserved.
Contradicting this idea...Count Rumford observed (1798) that a cannon could be repeatedly bored out (the hole drilled bigger), and each time it heated up.
Joule's experiment
1845 - James Joule made difficult measurements of the temperature increases of water in relationship to the change of mechanical energy of falling weights.

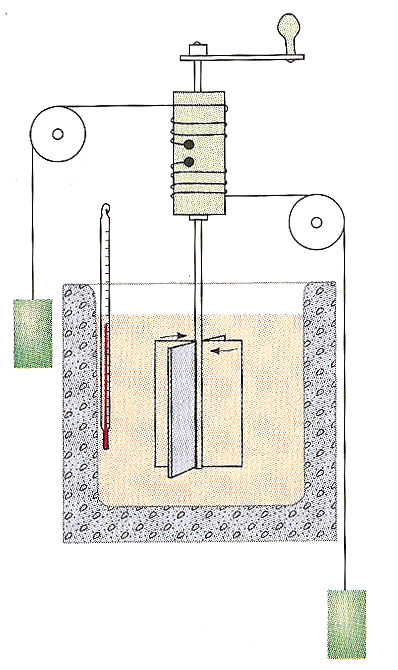
He found that the change of temperature of water in his insulated vessel could reproducibly be related to the mass' change of height according to the relationship $$\begineq -mg\Delta h &= m_wc_p\Delta T \endeq $$ where the constant $c_p=1$ calorie / degree C / gram.
...which started to convince people that heat is a form of energy, and paved the way for our modern understanding of...
Conservation of Energy
Much of analytical mechanics and general physics can be summed up by the law of conservation of energy:
The total energy of all the participants in any process remains unchanged throughout that process. That is, energy cannot be created or destroyed.
Energy can be transformed (changed from one form to another):
- Chemical energy,
- Gravitational potential energy,
- Nuclear energy,
- Heat,
- other forms...
Energy can be transferred (moved) from one body to another,
...but the total amount always remains the same.
The idea of conservation of energy has been hugely successful. Here, for example, is the story of the prediction and discovery of a completely unknown particle (the neutrino).
But what *is* energy? It's not exactly a material substance...
Beyond energy conservation
Joules' results can be expressed in terms of energy. If we say that the mechanical work done by the falling weights, $\Delta W$, was converted into an equal amount of energy in the form of "heat", $\Delta Q$, then there is an equation that relates that heat energy to a change in temperature, $\Delta T$:
$$\Delta W \rightarrow \Delta Q = m c_P \Delta T$$ where the "heat capacity" of water, for example, is $c_P$=1 cal/gm/${}^o$C.
But now consider the following experiment with water:
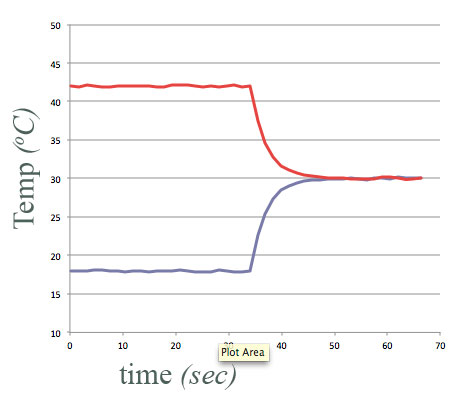 equal amounts of water, at different temperatures,
equal amounts of water, at different temperatures,
- Put in "thermal contact" at $t=34$ sec.
- Final temperature of each container of water is halfway between their initial temperatures.
 Energy conserved.
Energy conserved.
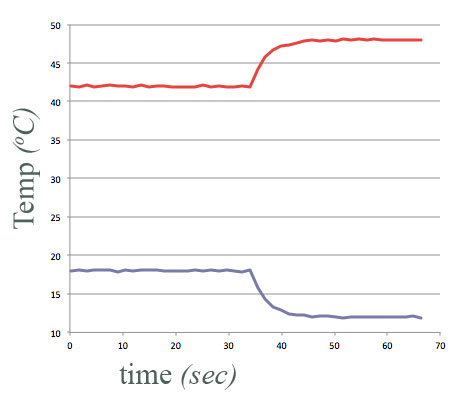 Think of same experiment...
Think of same experiment...
- Final temperature of each container of water changes by the same (but opposite) amount.
 Energy conserved.
Energy conserved.
But this scenario never happens in nature...
$\Rightarrow$ Something more than just energy conservation is needed to describe the patterns we see in nature.
This led, eventually, to the second law of thermodynamics which involves entropy -- a concept named only in the 19th century.
Thermodynamics and Statistical Mechanics
Both Thermodynamics and Statistical Mechanics cover the ground that we're interested in:
| Thermodynamics | Statistical Mechanics |
|---|---|
|
|
But the two theories are connected. We'll find eventually, for a system of idealized, billiard-ball like atoms of mass $m$, that the temperature of the system (a macroscopic variable) is related to the average kinetic energy of atoms (a microscopic variable): $$T \propto \frac{1}{2}mv_{\rm rms}^2.$$
From a practical engineering point of view, thermodynamics is attractive, since you don't have to keep track of $10^{20-50}$ variables.
But, we'd like to explain things in terms of more fundamental quantities: Statistical mechanics makes the connection between the "average" quantities of thermodynamics and the microscopic characteristics of atomic particles.
Image credits
Flickr users Omegaman, mdavidford, Taccola wheel, Mostafa Zamani, NASA/CXC/SAO