E-field + relativity = B-field
Using the Lorentz transformations, we shall find that a magnetic force in one inertial frame turns out to be an electric force in another frame.
So, apparently the electric and magnetic forces are not separate forces but one, with differing manifestations, depending on relative motion.
How fast is "current"?
The charge carriers in a copper wire are electrons. Imagine a copper wire:
- with a diameter of 1 mm,
- carrying a current of 1 amp.
How fast are the charge carriers (usually electrons) in a copper wire moving?
In the diagram below, there are charge carriers with a charge density $\rho$. The wire as a whole is neutral, so there is an equal and oppose charge density of stationary charges, but we're interested only in the mobile ones, in order to calculate the current.
The total charge, $Q$, crossing area $A$ in a time $t$, due to charge carriers with charge density $\rho$ moving with an average speed (drift velocity) $v_d$, is
$$Q = \rho A v_d t \Rightarrow Q/t = I = \rho A v_d.$$
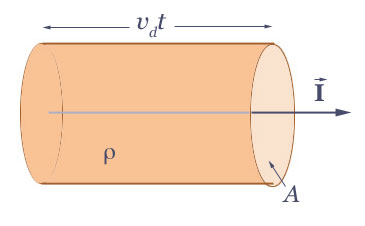
So... $$v_d=\frac{I}{\rho A}$$
- A typical wire has a diameter of about 1mm, so $$A=\pi r^2=\pi (.5\times10^{-3}
\text{ m})^2=8 \times 10^{-7} \text{ m}^2.$$
- A wire is typically made out of copper: atomic weight = 63.5 g/mole, density=8.94
g/cm^3. There is one free (conduction) electron per copper. So, the density of charge carrying electrons in copper is the same as the number density of atoms...
$$\begineq n&=\frac{8.94 \times 10^3\text{kg/m}^3* 6.02 \times 10^{23}\text{atoms/mole}}{63.5 \times 10^{-3}\text{kg/mole}}\\
&= 8.5 \times 10^{28}\text{free electrons/cubic meter}.\endeq$$
- The charge per unit volume is the number density times the charge of an electron:
$$\begineq\rho&=n e = 8.5 \times 10^{28} * 1.6\times10^{-19}\text{ C}\\
&= 1.4 \times 10^{10}\text{C/m}^3.\endeq$$
- A typical (well, actually, kind of high) current is 1 Amp = 1 C / s=$I$.
Putting this together... $$\begineq v_d &= \frac{I}{\rho A} = \frac{1 \text{C/s}}{1.4 \times 10^{10}\text{C/m}^3 * 8 \times 10^{-7} \text{m}^2}\\ &= 8.9 \times 10^{-5}\text{m/s}\approx 0.1 \text{mm/sec}=32 \text{cm/hr} .\endeq$$
The typical ballistic speed of a copper conduction electron (the Fermi velocity) between collisions with ions is $1.6 \times 10^6 \text{m/s}$. So the average velocity due to the current in this wire is much, much less, which is why it's called the drift velocity $v_d$.
Lorentz transform of a magnetic force field
From the r.h. rule for fields, and the r.h. rule for magnetic forces, we know that there is an attractive force between currents flowing in the same direction in parallel wires.
Now, we'll analyze the interactions of a current in one wire with one charge carrier moving parallel to the wire in two different reference frames.
Frame with no electric force
Consider a reference frame ${\cal B}$ moving at $v=v_d/2$, half the drift velocity, relative to the stationary wire.
In reference frame ${\cal B}$:
- There is also a charge, $q$, moving within the reference frame with a speed $v=v_d/2$ to the right,
- it appears that the negative charge carriers and the positive copper ion cores are moving with equal and opposite velocities.
- We can picture the negative and positive currents as line charges, with equal but opposite line charge densities.
- $q$ is moving to the right with the same speed as the positive line charge.
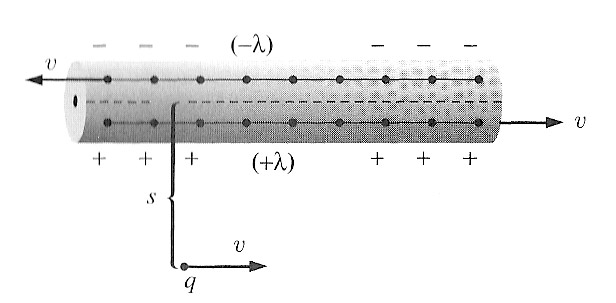
Cartoonifying the negative and positive charges as line charges, the total current is the sum of the positive current (directed to the right) $I_+=\lambda v$ and the current of the negative charges, which is also pointing to the right $I_- = \lambda v$. So $$I = 2\lambda v.$$
A single, positive 'test' charge (representing current in a parallel wire with the same drift velocity as the first wire), is a distance $s$ away, and is moving also with speed $v$ to the right (equal to the speed of the positive line charge).
In this frame, ${\cal B}$,
the electric fields due to the two equal and opposite line charges just cancel each other out. There is only a magnetic force on our moving test charge, $q$.
The test charge experiences only a magnetic force, proportional to its speed, $v$, and to the magnetic field $B$ of the wire. We know it's an attractive force of magnitude: $$F_m = qvB = qv\frac{\mu_0 I}{2\pi s}.$$
Frame with no magnetic force
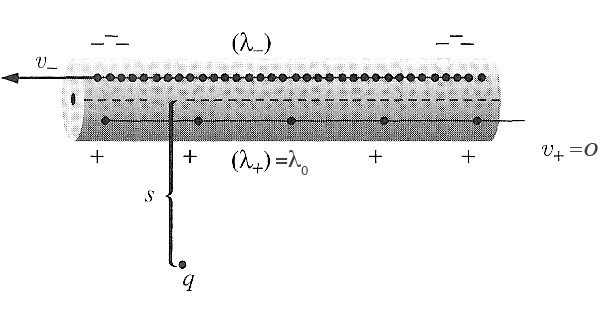
Consider an inertial frame $\cal{E}$, which is moving with speed $v=v_d/2$ to the right with respect to frame $\cal{B}$.
In reference frame ${\cal E}$:
- The positive line charge (the copper ion cores), and the test charge, $q$, are both at rest in $\cal{E}$.
- Since the test charge is at rest in this frame, it cannot have any magnetic $\myv v \times \myv B$ force acting on it, because its velocity is 0.
- The negative line charge is in motion, so it appears to be Lorentz contracted. Therefore $|\lambda_-| \gt |\lambda_+|$. The wire no longer appears neutral, so there is an electrical force on $q$
We know that with realistic numbers, the drift velocity is less than mm/s. It doesn't seem like there should be *any* force acting on the test charge.
Why should changing our point of view by millimeters per second give us either some force or no force?
AWKWARD!
But from the point of view of special relativity, since the $\lambda _-$ line charge is moving in this frame, there should be a length contraction of that line charge, and there is ever so slightly more negative charge than positive charge (per unit length of the wire). This would give rise to a very slight electrical attraction between the conductor and the motionless, positive test charge. How much??
Using Gauss' law (if you forget) to figure the force from an infinite line charge, $$F_e = -q \frac{\lambda _{-} - \lambda _+}{2\pi \epsilon_0 s}.$$
Let's figure these quantities in more detail.
The speed $v_+ = 0$. The speed $v_-$ of the negative line charge can be found from our relativistic velocity addition formula: $$v_{x {\cal b}} = (v_{x {\cal m}}+V)\frac{1}{1+Vv_{x {\cal m}}/c^2}.$$ In ${\cal M}$ its speed was $v=v_d/2$. And ${\cal M}$ was moving with speed $V=v$ relative to ${\cal E}$: $$v_- = (v+v)\frac{1}{1+(v v)/c^2} = \frac{2v}{1+v^2/c^2}.$$
In $\cal{E}$, the positive line charge is at rest, so call $\lambda _+\equiv\lambda_0$. The charge density of the negative line charge is: $$\lambda_- = \gamma_-\lambda_0 = \frac{\lambda_0} {\sqrt{1-v_-^2/c^2}}.$$
In the other frame, $\cal{B}$: $$\lambda = \gamma \lambda_0 = \frac{\lambda _0}{\sqrt{1-v^2/c^2}}$$
Biting the algebraic bullet, we substitute the the expression for $v_{-}$ into the one for $\lambda _{-}$:
Then the difference...
$$\begineq \lambda _{-} - \lambda _{+} &=\lambda _{-} - \lambda_0 = \lambda _0\left[ \frac{c^2+v^2}{c^2-v^2} -1\right] \\ &= \lambda_0 \left[ \frac{2v^2}{c^2-v^2} \right] = \lambda_0 \left[ \frac{2v^2/c^2}{1-v^2/c^2} \right] \\ &=\frac{\lambda_0}{\sqrt{1-v^2/c^2}}\left[ \frac{2v^2/c^2 }{\sqrt{1-v^2/c^2}} \right]\\ \lambda _{-} - \lambda _{+} &= \lambda \left[ \frac{2v^2/c^2 }{\sqrt{1-v^2/c^2}} \right].\endeq$$
We're trying to calculate the electrical force in this reference frame: $$\begineq F_e &= -q \frac{\lambda_- - \lambda_+}{2\pi \epsilon_0 s} \\ &= - \frac{\lambda v}{\pi \epsilon_0 c^2 s} \frac{qv }{\sqrt{1-v^2/c^2}} \endeq$$
I wanted to make sure that I didn't throw any term away before taking the difference between the two line charge densities. But now, taking into consideration the very small value for $v_d$, I'll approximate this electric force as... $$F_e \approx -\frac{\lambda v}{\pi \epsilon_0 c^2 s} qv .$$
In SI units
- $\epsilon_0= 8.85418782 \times 10^{-12}\ \frac {C^2}{Nm^2}$.
- $\mu_0=4\pi \times 10^{-7}\ \frac{N}{A^2}$.
- It just so happens that $\sqrt{1/(\epsilon_0 \mu_0)} = 2.99863 \times 10^8 \ m/s=c$.
Now, taking into account that, in frame ${\cal B}$ we had $I = 2 \lambda v$, we find this relationship between the magnitudes of the two forces $$\begineq |F_e| \ \text{in}\ {\cal E}&= \frac{\lambda v}{\pi \epsilon_0 c^2s} qv \\ &= qv \frac{\mu_0 I}{2\pi s}=|F_m|\ \text{in}\ {\cal B}.\endeq$$
In reference frame ${\cal E}$
There is no magnetic force, only an electric force. But the electric force, in ${\cal E}$ and the magnetic force in ${\cal B}$ are equal.
So it turns out that even for speeds much, much smaller than relativistic speeds, we have a force that's the same in two reference frames, but it appears to be an an electric force in one frame, and appears to be a magnetic force in another.
I have glossed over a couple of issues, such as how forces transform, and whether or not charge dilates or contracts in different frames. (It doesn't.)
Summary
For a positive test charge moving with speed $v_d/2$ in the same direction as the current in a nearby wire,
- We found one reference frame in which there is only a magnetic force acting on the test charge, and
- one reference frame in which there is only an electric force acting.
- The magnitude of the force acting on the test charge was the same
This supports the contention that the electric and magnetic forces could be considered as two aspects of a unified "electromagnetic" force:
$\Rightarrow$ The electromagnetic force acting on a charged particle (but not the electric or magnetic forces on their own) is relativistically invariant. It's the same in all reference frames.