Lorentz transformations
Read Griffiths' [12.1]. This material follows John R. Taylor, "Classical Mechanics"-Chapter 15.
- 'Events'
- Simultaneity
- Transforming speeds
'Events'
Imagine an event, such as the impact of a tomato on the train car.
... (thrown by an over-exuberant supporter, joyfully sharing the
bounty of her garden, no doubt!).
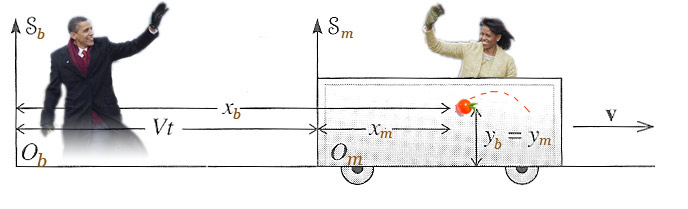
Such an event happens at a particular position and a particular time.
Barack sees this as happening at $(x_{ {\cal b}},y_{ {\cal b}},z_{ {\cal b}},t_{ {\cal b}})$, and Michelle at $(x_{ {\cal m}},y_{ {\cal m}},z_{ {\cal m}},t_{ {\cal m}})$. We'd like the equations that connect these two sets of coordinates/times.
The two coordinates perpendicular to the relative velocity have no contraction/dilation, and so...
$$ y_ {\cal m} = y_{ {\cal b}},$$ $$ z_{ {\cal m}} = z_{ {\cal b}} .$$
Michelle is stationary wrt the mark on the side of the car. Taking her coordinate for the tomato impact as the proper length, then Barack sees a contracted length related to the proper length by... $$x_{ {\cal b}}-tV_{ {\cal b}} = x_{ {\cal m}}/\gamma.$$
Re-arranging lightly:
$$x_{{\cal m}} = \gamma \left(x_{ {\cal b}}-Vt_{ {\cal b}}\right).$$
Now, imagine the tomato lands on the platform instead of on the train. Following the same line of argument (or, just exchanging subscripts and substituting $-V$ for $V$), we'd have, $$x_{ {\cal b}} = \gamma\left(x_{ {\cal m}}+Vt_{ {\cal m}}\right).$$
Substituting this equation into the one above to eliminate $x_{ {\cal m}}$ and solve for $t_{ {\cal m}}$:
$$ t_{ {\cal m}} = \gamma(t_{ {\cal b}}-Vx_{ {\cal b}}/c^2).$$
These four (highlighted) equations are the Lorentz transformations.
Historically, the Lorentz transformations preceded the assumption that the speed of light is the same for all observers.
Lorentz put forth these transformations as an alternative system in which the equations of Newtonian mechanics are invariant, and which also "explained" the Michelson-Morley experiment: A length contraction of the apparatus in the direction of motion would explain why no change in the speed of light was seen. It took Einstein, a few years later, to interpret these transformations in terms of his assumptions about special relativity.
Simultaneity
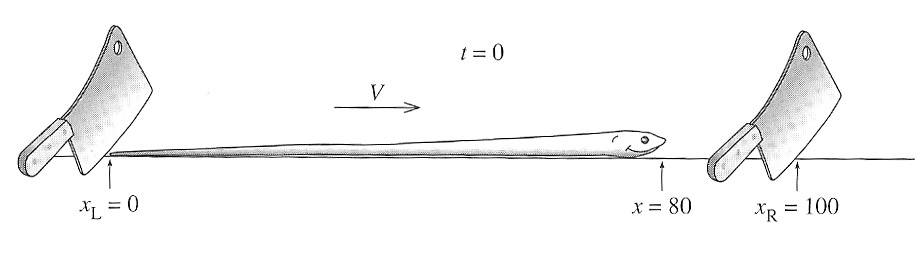
A snake with a proper length of 100 cm is travelling across a table at $V=0.6c$.
The snake's owner decides to "tease" the snake by bouncing two cleavers separated
by a meter when the snake's tail is just past the back cleaver, reasoning that
"After all, $\gamma=1/\sqrt{1-V^2/c^2} = 5/4$, so my snake should have a contracted
length of 0.8 m, and he'll be unhurt".
Meanwhile the snake frets thusly: "Those cleavers are approaching me at 0.6c, so the distance between them is just 0.8m in my reference frame, less than the distance from my tail to my one-and-only head. "
"I'm gonna die!".
Use the Lorentz transformations to reassure the snake (or not)...
In the $ {\cal b}$ frame of the owner, the left and right cleavers drop at:
$(x_{L}, t_{L})=(0,0)$ and
$(x_{R}, t_{R})=(1.0,0)$.
Now, using the Lorentz transforms to find the coordinates in the snake's $ {\cal m}$
frame: The left cleaver drops at:
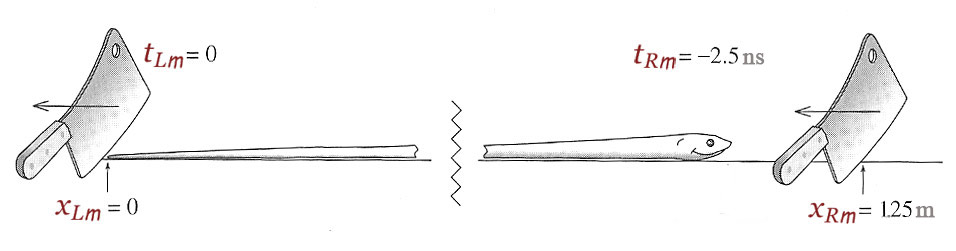
$x_{L {\cal m}} = \gamma(x_{L}-Vt_{L})=0$ m, and
$t_{L {\cal m}} = \gamma(t_{L}-Vx_{L}/c^2)=0$ s.
What about that all-important right cleaver? [Use the Lorentz trafo to calculate $(x_{R{\cal m}},t_{R{\cal m}})$]
$t_{R {\cal m}} = \gamma(t_{R}-Vx_{R}/c^2)=\frac{5}{4}(0-.6c(1m)/c^2)= -2.5 \text{ ns}$.
Oh, the right one has dropped (and come up) 2.5 nanoseconds before the left one, so the cleaver drops are not simultaneous in the two frames.
The position in the snake's frame of the second cleaver, $x_{R {\cal m}}$ when dropped was:
$x_{R {\cal m}} = \gamma(x_{R}-Vt_{R})=\frac{5}{4}(1.0-0)=1.25$ m.
Does that length difference of 1.25 m contradict the length contraction that the snake was counting on for lengths?
To measure the distance between
the cleavers, the snake should not be looking at where the right cleaver is
at $t_m=-2.5$ ns, but rather at $t_m=0$. (At that time, the left cleaver is at $x_m=0$ m.). So, 2.5 ns *after* the right cleaver comes down/goes up (which is $t_m=0$ s for the snake), What is the position of the right cleaver?
Use this information to make two sketches, from the snake's point of view, of where both cleavers are at $t_m=-2.5 ns$ and at $t_m=0 ns$.
The the right cleaver has moved to...
$x_{r {\cal m}}(t_{ {\cal m}}=0) = 1.25$ m $ - (0.6c)(2.5$ ns$) = 1.25$ m $ - 0.45$ m $ = 0.8$ m.
...an 80% length contraction of the distance between the cleavers, as the snake correctly assumed.
By the way, in one nanosecond, light travels:
$\Delta x = 3.0\times10^8 \text{ m/s } * 1 \text{ ns } = 0.3$ m $ = 11.7$ inches.
So, you might remember the foot as a pretty good approximation to a "light-ns".
For example, GPS receivers which depend on timing the arrival of E-M waves from the GPS satellites need time resolutions of about 1 ns to achieve a spatial resolution of a foot.
Transforming speeds
Einstein's velocity transforms follow from taking derivatives. For speeds in the direction of the relative velocity...
From Barack's point of view...
$$v_{x {\cal b}} = (v_{x {\cal m}}+V)\frac{1}{1+Vv_{x {\cal m}}/c^2}.$$
...Looks like Galilean transform as long as $Vv \ll c^2$.
Read example 12.2 - The twin paradox.
Image credits