Relativity (mostly special)
Absolute, true, and mathematical time, of itself and from its own nature, flows equably without relation to anything external.
-Isaac Newton
It came to me that time was suspect!
-Albert Einstein
Outline
- Galilean transformations of velocity
- Invariance of physical laws
- Breakdown of Galilean tranformations
- Einstein's resolution
- Time dilation
- Length contraction
- Experimental evidence?
The physical laws we're familiar with (e.g. $\myv F = m\myv a$) remain unchanged (are invariant)...
- in different locations,
- at different times,
- for different orientations,
Einstein added...
- at different speeds. [as long as acceleration=0].
Galilean transformations
Galilean transormations Part 1 Narrated ~6 min
Galileo was already familiar with this way of transforming from one moving
reference frame to another...
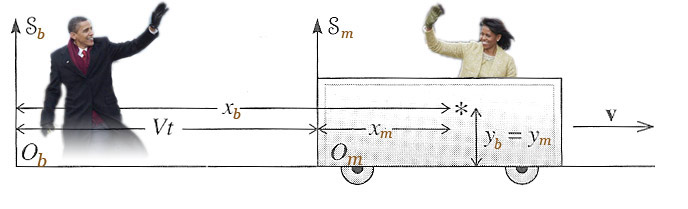
We'll have Barack (frame ${\cal b}$) standing on the platform of a railway station, while Michelle (frame ${\cal m}$) is in a train car moving in the $x$ direction with a constant speed $V$. Their origins coincide at $t=0$. $$y_{\cal m} = y_{\cal b}$$ $$z_{\cal m} = z_{\cal b}$$ $$t_{\cal m}=t_{\cal b}.$$ $$x_{\cal m} =x_{\cal b} - Vt$$
When it's clear from context, we shall frequently drop the ${\cal b}$ subscript from the platform quantities.
If an object on the platform is moving with a velocity $v_{x {\cal b}}$, then its speed with respect to the train is (take $\del/\del t$ of the relationship for the $x$ direction): $$v_{x {\cal m}} = v_{x {\cal b}} - V.$$
Galilean transformations
Galilean transformations Part 2 Narrated ~4 min
Consider two billiard balls with equal mass moving towards each
other, then we know that they'll rebound off each other with the same speed.

Together with Galilean relativity, (at 5 f/s to each
ball) we can figure out what happens if one ball is incident on a stationary
one...

OK, OK, this is something you can also figure out from energy/momentum conservation.
Here is a collision that is a bit harder to find, even if you know a bunch of conservation laws.
A light ball will rebound off a much heavier one with practically
the same speed as it came in with.

But what if the heavy ball is moving towards a much lighter ball. What will the outcome of the collision be?

Invariance of physical laws under transformation
Here is the transformation law for $x$ positions: $$x_{{\cal m}}=x_{{\cal b}}-Vt$$ So, let's say that Michelle undertakes a measurement of the acceleration ($a_{x{\cal m}}$) in her reference frame. Taking the second derivative of both sides of this equation, and multiplying both sides by the mass $m$.. $$\begineq m \frac{d^2 x_{ {\cal m}}}{dt^2} &= m \frac{d^2}{dt^2}(x_{{\cal b}}-Vt) = m \frac{d^2 x_{ {\cal b}}}{dt^2}\\ ma_{x {\cal m}} &= m a_{x{\cal b}}\\ \Rightarrow F_{xm}&=F_{xb} \endeq$$
If she accelerates something in the $y$- direction, since $y_m=y_b$ it's even easier to see that: $$F=m \frac{d^2 y_{\cal m}}{dt^2} = m \frac{d^2 y_{b}}{dt^2} .$$
So the force law takes the same (invariant form) $\myv F= m \myv a$ in both frames.
Galileo used the argument that no experiment could tell whether the earth was still (and the sun moving) or the earth was moving (and the sun was still) in support of Kepler's model of a heliocentric solar system.
Breakdown of Galilean transformations
Two results from electromagnetism do not 'fit' with the Galilean transformations at all:
 Speed of light: The four Maxwell equations predict electromagnetic waves (light) that move
at a speed $c$ in all reference frames!
Speed of light: The four Maxwell equations predict electromagnetic waves (light) that move
at a speed $c$ in all reference frames!
Not at $c$ relative to the velocity of the flashlight that
I just turned on. Just $c\,$!! How can that be?
The second case is the forces between two charges: in different reference frames ...
Imagine that there are two pieces of charge glued to Michelle's train car:
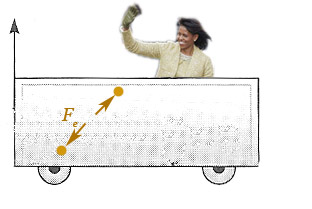
Michelle
says:
"There's an electric force between those two charges. But they're not moving, I don't see any currents, so there's no magnetic force."
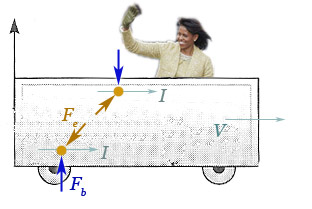
Meanwhile Barack (on the platform) sees the charges on a moving train car and
says:
"Yes,
honey, there's an electric force. But you're moving, so each charge is generating a magnetic field.
Since there's a magnetic field. There's also a magnetic force between those two charges!".
As pictured, there's also a torque. Trouton and Noble tried and tried to detect this torque (ca. 1902) but in vain.
Einstein's resolution
Lorentz had come up with an alternative set of transformations to Galileo's which worked for E-M fields, but with no justification.
Einstein proposed these two Ansätze (postulates) as starting points from which to justify Lorentz's math ("Zur Elektrodynamik bewegter Körper")
- The laws of physics [Einstein said Mechanics and Electro-Magnetism] are the same in all inertial reference frames*: absolute uniform motion cannot be detected.
- The speed of light $c$ is the same no matter the motion of the source.
*An inertial reference frame is one with no acceleration: Newton's law $\myv F=m \myv a$ holds in any inertial reference frame, but not (strictly) in a rotating reference frame like earth, or in an accelerating car.
We shall now explore some of the strange consequences (and experimental evidence) of these assumptions:
$\Rightarrow$ Time cannot be the same for all observers, and neither can length, if we'd like to stick to Einstein's postulates.
Time dilation
Time dilation Narrated ~4 min
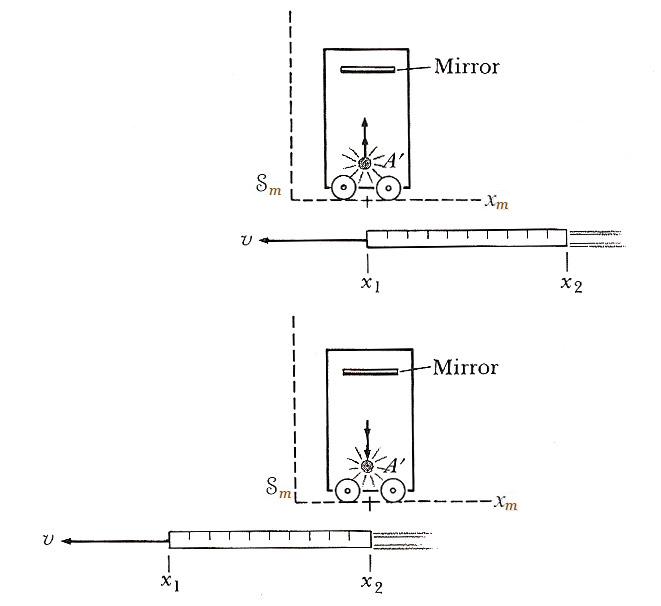
Imagine flashing a bulb at position $A'$ in the train, and timing it until
its return after bouncing off a mirror a distance $D$ above.
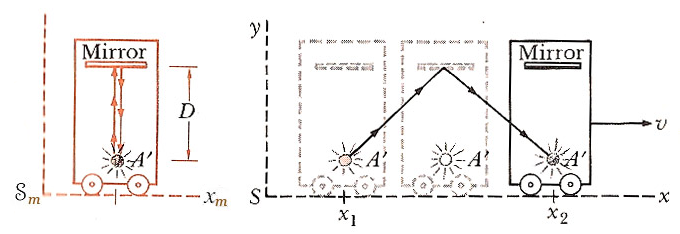
Michelle sees the situation at the left and measures the time for a light flash to return to $A'$ as $$\Delta t_{\cal m} = \frac{2D}{c}.$$
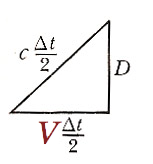 Meanwhile,
Barack measures a time interval $\Delta t$ for the emission-bounce-return to
happen. We're going to assume [Einstein] that $c$ is the same for Barack as for Michelle.. Then using this triangle...
$$(c \frac{\Delta t}{2})^2 = D^2 + (V \frac{\Delta t}{2})^2.$$
Meanwhile,
Barack measures a time interval $\Delta t$ for the emission-bounce-return to
happen. We're going to assume [Einstein] that $c$ is the same for Barack as for Michelle.. Then using this triangle...
$$(c \frac{\Delta t}{2})^2 = D^2 + (V \frac{\Delta t}{2})^2.$$
Solving for $\Delta t$: $$\Delta t = \frac{2D}{\sqrt{c^2-V^2}} = \frac{2D}{c} \frac{1}{\sqrt{1-V^2/c^2}}.$$
Using Michelle's time interval: $$\Delta t = \gamma \Delta t_{\cal m}$$ where: $$\gamma \equiv \frac{1}{\sqrt{1-V^2/c^2}} \geq 1.$$
Michelle can use the same clock to measure the starting pulse and the return.
But because the flash and return happen at different locations on the platform,
Barack has to use two previously synchronized clocks to measure the time.
The time in the frame in which just one clock can be used is called the proper time.
The proper time is always shorter than the time between these two events in any other frame. Folks moving with respect to the light pulse see events taking longer--a phenomenon called time dilation.
Length contraction
Length contraction Narrated ~2.5 min
Imagine that in the experiment above, a measuring scale was fixed to the platform. The ruler has its proper length $L_0$ in the frame (${\cal b}$) in which it is at rest.
What length do folks on the train attribute to the ruler?
Michelle sez':
"It took a time $\Delta t_{\cal m}$ for something moving at a speed of $V$ to
pass by. It must have had a length":
$$L_{\cal m}=V\Delta t_{\cal m} = V \frac{\Delta t}{\gamma} = \frac{L_0}{\gamma}.$$
So everybody moving relative to the ruler measures the ruler to be somewhat shorter than its proper length. This is the length contraction.
Length contraction only happens in the direction of motion--not in a direction ($y$- or $z$-direction) perpendicular to the motion.
Experimental evidence?
Muons ($\mu^-$) are unstable particles that decay in the lab according to $$N(t)=N_0e^{-t/\tau}$$ with $\tau=2 \times 10^{-6}$ sec in a laboratory (where the muon is at rest).
They are produced high in the atmosphere as a by-product of cosmic rays hitting the atmosphere:
high energy $p^+$ $\to\ \pi$ meson ($\tau=3\times 10^{-8}$ s) $\to\ \mu^-$ ($\tau=2\times 10^{-6}$ s).
Muons have approximately the same momentum as the original proton, but a much smaller mass (~1/9) so will be moving faster than the original proton. Let's say that a particular population of muons have a speed of 0.998$c$. Then without special relativity, a muon with the mean lifetime should travel just $0.998 (3 \times 10^8 \text{m/s})*2 \times 10^{-6} s = 600 m$.
Muons are not produced lower in the atmosphere: The cosmic protons are charged particles (89% protons), which interact strongly with matter. So no cosmic ray protons penetrate beyond the outer layers of the atmosphere. (Fortunately for life on earth: If you though UV radiation was bad for your skin, imagine what it would be like to be hit by high energy protons!)
So, if muons are produced several thousand meters up in the atmosphere, very few should reach sea-level.
But if special relativity is true, then the lifetime of a muon measured by an observer stationary on the surface of the earth should be longer by a factor $\gamma =\frac{1}{\sqrt{1-V^2/c^2}}$. We have $\gamma(0.998c) \approx 16$, so it should appear to have a longer lifetime of $\approx 30 \times 10^{-6}$s, during which it travels 9000 m.

Or, from the point of view of the muon, the distance 9000 m is contracted
in its reference frame to just 600 m. So, at 0.998$c$ (heck, let's just call the speed ~$c$) it takes $\Delta t=600m / c=600m/3\times 10^8m/s=2\times 10^{-6}$s which is about the same as its
$2\times10^{-6}$s half-time for decay.
Measurements show the concentrations of muons high in the atmosphere and close to sea level are of the same order of magnitude.
Calculate: Barbara is on Earth. Arnold is on a rocket passing close to Earth at speed $V$. As Arnold passes over Goshen, he times how long it takes to pass from one end of the Goshen Airport landing strip to the other end. That works out to 1.833 km long, and he sends this information to Barbara by HyperNet. Barbara looks up the length of the runway, which is 1844 m, and (assuming that Arnold was able to make such precise measurements) works out Arnold's speed as: $$V=???$$
$$\frac Vc=\sqrt{1-(1.833/1.844)^2}=0.109$$