Optics
What emerges when we combine our wave solutions with the boundary conditions on the fields at interfaces between different materials? This turns out to be all we need to derive the phenomena of reflection and refraction.
Boundary conditions
We examined the boundary conditions at an interface between dielectrics. When there's no free charge around: $D_{\perp}-D'_{\perp}= \epsilon E_{\perp}-\epsilon' E'_{\perp}= \sigma_f\to 0$, so $$\epsilon E_{\perp}=\epsilon' E'_{\perp}$$ and $$E_{\parallel}=E'_{\parallel}.$$
There are also boundary conditions between magnetic materials. With no free currents around: $$B_{\perp}=B'_{\perp}$$ and $$\frac{1}{\mu}B_{\parallel}=\frac{1}{\mu'}B'_{\parallel}.$$
Normal incidence
If a plane E-M wave "$I$" is incident from material
1 to material 2 at normal incidence (pictured) to the interface conveniently
located at $z=0$, we expect that there should also be a transmitted wave
solution, $T$, and perhaps a reflected wave $R$ as well. Without any loss of generality, let's say that the incident wave is polarized in the $\uv x$ direction:
$$\begin{array}{l}
\myv E_I ={\cal E}_Ie^{i(k_1z-\omega t)}\uv x, \\
\myv B_I =\frac{1}{v_1}{\cal E}_Ie^{i(k_1z-\omega t)}\uv y
\end{array}$$
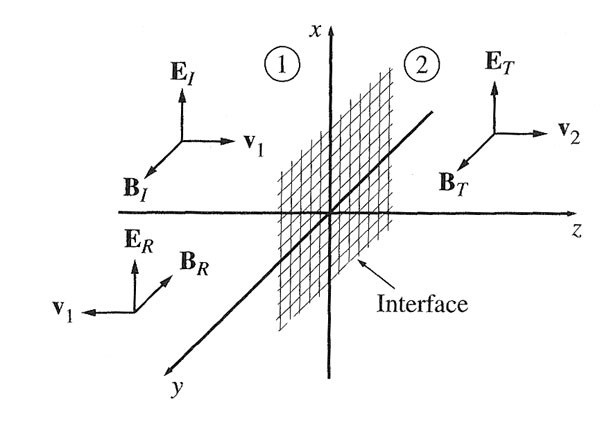
The reflected wave: $$\begin{array}{l} \myv E_R ={\cal E}_Re^{i(-k_1z-\omega t)}\uv x, \\ \myv B_R =-\frac{1}{v_1}{\cal E}_R e^{i(-k_1z-\omega t)}\uv y. \end{array}$$
The transmitted wave: $$\begin{array}{l} \myv E_T ={\cal E}_Te^{i(k_2z-\omega t)}\uv x, \\ \myv B_T =\frac{1}{v_2}{\cal E}_Te^{i(k_2z-\omega t)}\uv y. \end{array}$$
Applying the four boundary conditions at the interface at $z=0$:
- No perpendicular component of $\myv E$ on either side,
- $$\begineq E_{\parallel}&=E'_{\parallel}\\ E_{Ix}(z=0)+E_{Rx}(z=0)&=E_{Tx}(z=0)\\ {\cal E}_I +{\cal E}_R &= {\cal E}_T.\endeq$$
- No perpendicular component of $\myv B$ on either side,
- $$\begineq \frac{1}{\mu}B_{\parallel}&=\frac{1}{\mu'}B'_{\parallel}\\ \frac{1}{\mu_1v_1}\left({\cal E}_I - {\cal E}_R\right) &=\frac{1}{\mu_2v_2}{\cal E}_T. \endeq$$
With 2 equations for 3 unknowns, we can get solutions for ${\cal E}_T$ and ${\cal E}_R$ in terms of the incident amplitude ${\cal E}_I$: $${\cal E}_R=\left( \frac{1-\beta}{1+\beta}\right){\cal E}_I,\text{ and } {\cal E}_T=\left( \frac{2}{1+\beta}\right){\cal E}_I.$$ where, $$\beta \equiv \frac{\mu_1v_1}{\mu_2v_2} = \frac{\mu_1n_2}{\mu_2n_1} \approx\frac{n_2}{n_1},$$ since it turns out that for most media, $\mu\approx \mu_0$.
Using our result that the intensity of a plane E-M wave is $I=(1/2)\epsilon v {\cal E}^2$, we can calculate the fraction of power in the incident wave which is reflected: (the reflection coefficient, $R$) $$R\equiv \frac{I_R}{I_I}=\frac{{\cal E}_R^2}{{\cal E}_I^2}=\left(\frac{1-n_2/n_1}{1+n_2/n_1}\right)^2.$$ [Calculate $R$ for $n_1=n_\text{air}=1$ and $n_2=n_\text{glass}=1.5$...]
The transmission coefficient, $T$ is: $$T\equiv \frac{I_T}{I_I}=\frac{{\cal E}_T^2}{{\cal E}_I^2}=\left(\frac{2}{1+n_2/n_1}\right)^2.$$ [What is that for transmission from air into glass?]
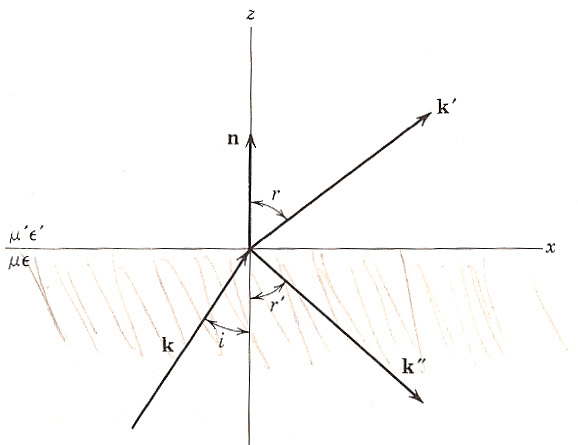
Oblique incidence
Atomic scattering
The atomic scattering factor for an isolated atom can be written as $f=f_1+if_2$. See henke.lbl.gov/optical_constants/intro.html. Using this, the atomic photoabsorption cross section, $\mu_a$ is $$\mu_a=2r_0\lambda f_2$$
Here, $r_0=$ is the classical electron radius, and $\lambda$ is the x-ray wavelength.
For a compound material, find the average, for example, for calcite CaCO${}_3$: $$\bar{f_2} = \frac{f_{2}^{\rm Ca} + f_{2}^{\rm C} + 3 f_{2}^{\rm O}}{5}$$
The fraction of an x-ray beam $T$ transmitted through a slab of material of thickness $d$ is $$T=e^{-n \mu_a d}$$
Where $n$ is the number of atoms per unit volume.
Physical constants
Avogadro's number: $N_A = 6.022\times 10^{23}$ [atoms] / mol
Classical electron radius: $r_0=2.818\times 10^{-15}$ m
For MoK${}_{\alpha 1}$ radiation... $\lambda=0.7093$ Angstrom, $E=17.44$ keV
Carbon: Cullity sez for graphite $\rho=2.27$ g/cm^3, and $\mu/\rho=0.5348$ cm^2/gm
Ca: $\rho=1.53$, $\mu/\rho=19.00$
O: $\rho=1.332\times 10^{-3}$, $\mu/\rho=1.147$