Maxwell's displacement current
Ampere's Law (1826)
In which Maxwell fixes a niggling inconsistency in Ampere's Law, $$\oint_{\cal C} \myv B\cdot d \myv \ell= \mu_0 I_\text{enc}.$$
For an ~infinite wire: $\Rightarrow
B = \frac{\mu_0 I}{2\pi r}.$
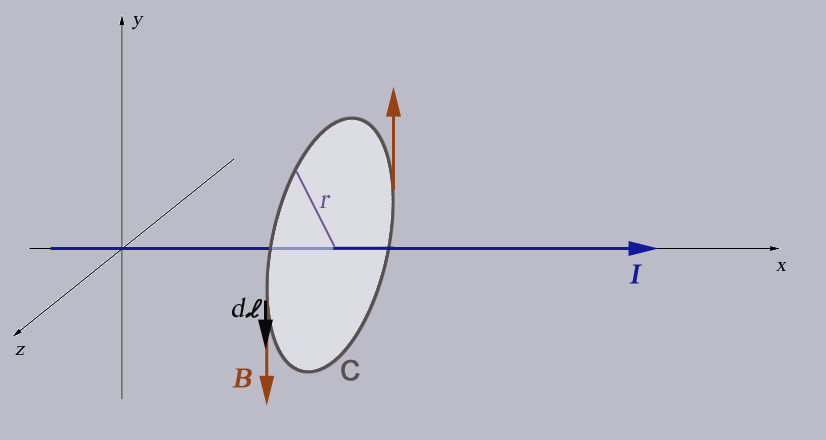
Remember that it doesn't matter *what* surface we use to figure $I_\text{enc}$:

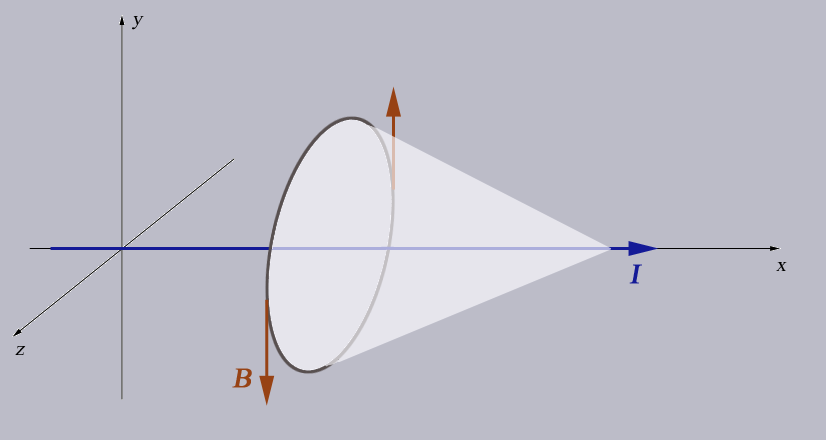
Maxwell notices a problem (1861)
We can arrange to have current $I(t)$ in the wire while we charge a capacitor.
Then you'd think $B(t)=\mu_0 I(t)/(2 \pi r)$,
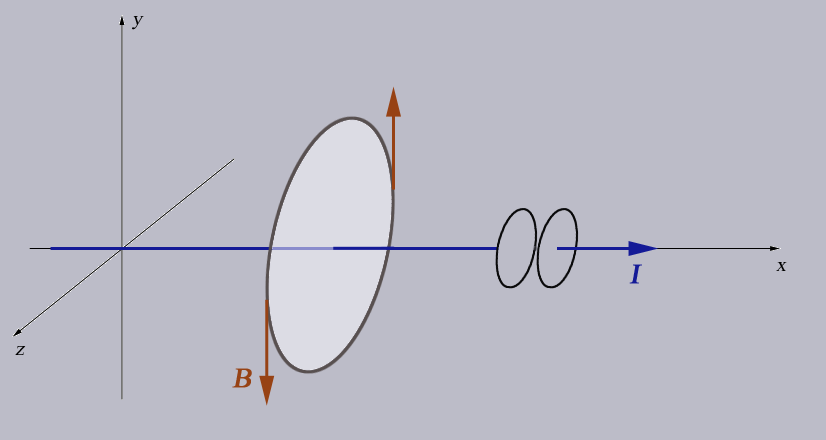
But with this surface, $I_\text{enc}=0\Rightarrow B=0$.
???
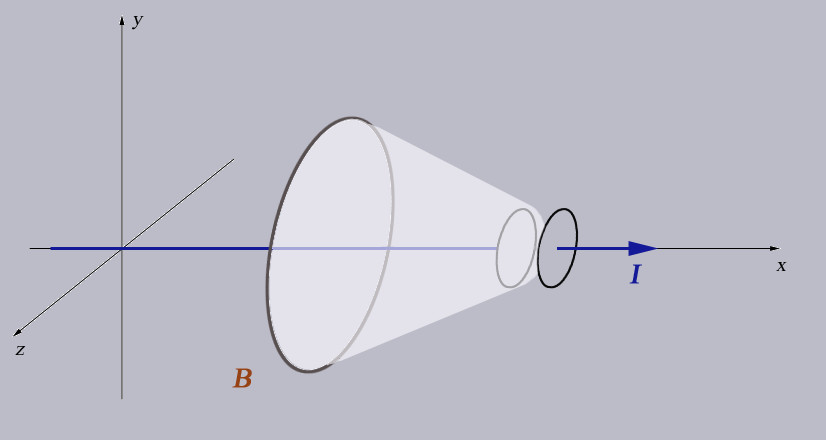
Maxwell's proposed resolution
If $I$ is the current flowing into (and out of) the capacitor, and we draw our surface ${\cal S}$ in between the plates where certainly $I=0$,
we'd like something that...
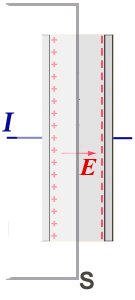
| penetrates the surface like $I$ would: | $$\int_{\cal S} \myv E\cdot d\myv a$$ |
| is proportional to $I$: | $$\frac{d}{dt}\int_{\cal S} \myv E \cdot d\myv a$$ |
| is equal in magnitude to (and has the same units as) $I$: | $$\epsilon_0 \frac{d}{dt}\int_{\cal S} \myv E \cdot d\myv a$$ |
Modified Ampere's law
$$\oint_{\cal C}\myv B \cdot d \myv \ell= \mu_0 I + \mu_0 \epsilon_0 \frac{d}{dt}\int_{\cal S} \myv E \cdot d\myv a $$
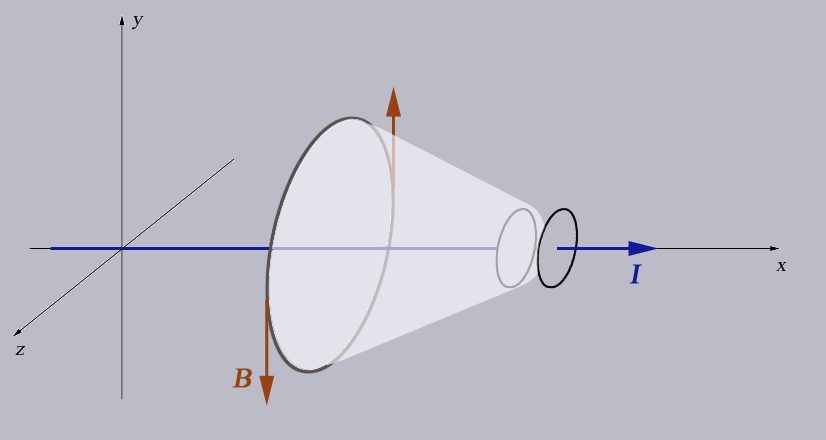
In order to recover the differential relationship from Ampere's law, We use Stoke's Law to re-write the left side of Ampere's Law as a surface integral... $$\int_{\cal S}\myv \grad \times \myv B \cdot d\myv a = \int_{\cal S}\mu_0 \myv J\cdot d\myv a + \int_{\cal S}\mu_0 \epsilon_0 \frac{\del}{\del t} \myv E \cdot d\myv a $$
This implies that the arguments of each of the surface integrals obey...
$$\myv \grad \times \myv B = \mu_0 \myv J + \mu_0 \epsilon_0 \frac{\del}{\del t} \myv E. $$ Maxwell's equation for $\myv \grad \times \myv B$.
In a linear dielectric/magnetic medium we have $$\myv{D}=\epsilon\myv{E}\ \hbox{ and }\ \myv{H}=\frac{1}{\mu}\myv{B}$$
So we could re-write this expression for a magnetic/di-electric medium as... $$\myv{\nabla}\times \myv{H} = \myv{J}_f+\frac{\del \myv{D}}{\del t}.$$