Electromotive force
Up until now, we've been doing electrostatics and magnetostatics, but it's time to let things start to move...

Electrostatics was characterized by: $$\myv \grad \times \myv E = 0,$$ in integral form (using Stokes' theorem) this is $$\oint_{\cal C} \myv E \cdot d \myv l = 0.$$
This might *not* vanish when things start to move... $$\oint_{\cal C} \myv E\cdot d \myv l \equiv \text{emf}\equiv {\cal E},$$ where $emf$ is the so-called electromotive force. Sorry this is horrible terminology because...
- $emf$ is not a force. $\myv E$ is a force per unit charge and,
- $emf$ is not even a force per unit charge, but rather the integral of a force per unit charge times a distance. Force times distance is energy.
So $emf$ is actually some sort of energy (work) per unit charge. It has the same units as a voltage.
Wire dragged through a magnetic field
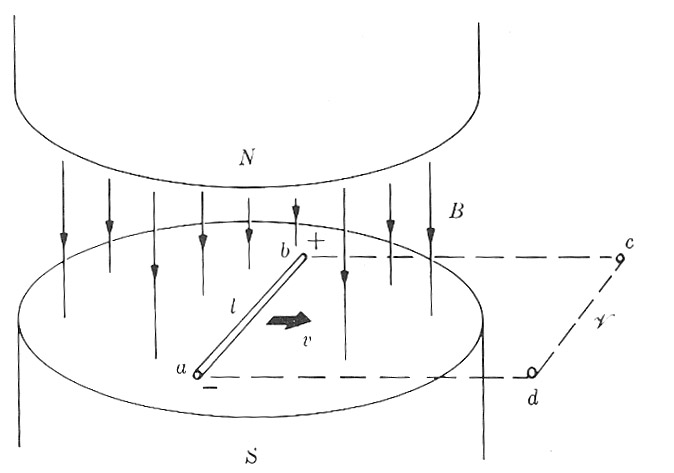 Consider a conducting wire being dragged through a constant magnetic field with a constant velocity.
Consider a conducting wire being dragged through a constant magnetic field with a constant velocity.
The Lorentz force comes into play:
$$\myv F = q(\myv v \times \myv B + \myv E).$$
Since there is charge in the wire some of which is free to move, the Lorentz force will push some of the charge to the ends of the wire (as shown).
Charge will stop moving when there is a balance inside the wire between the electric force due to accumulated charges at the ends of the wire, and the Lorentz force due to the motion of the wire:
$$E = vB$$.
So there is a potential difference between $a$ and $b$ of: $$\Delta V = \int_a^b \myv E \cdot d \myv l = El = Bvl.$$ If conductors were attached and run along $bc$ and $ad$, then this voltage appears across $cd$, and could drive a current through a resistor attached across $cd$.
Another point of view (G Phys) is that a voltage arises equal to the change of the magnetic flux enclosed by a loop: $$\Phi_m \equiv \int_{\cal S} \myv B \cdot d \myv a,$$
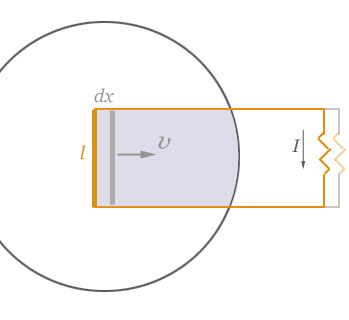 With a constant magnetic field, the magnetic flux is $B$ times the colored area in the diagram.
With a constant magnetic field, the magnetic flux is $B$ times the colored area in the diagram.
The flux is changing at the rate $$B\frac{dA}{dt} = -B\frac{l\, dx}{dt} = -Blv.$$ That is to say, the voltage is: $$\Delta V = -\frac{d}{dt}\Phi.$$
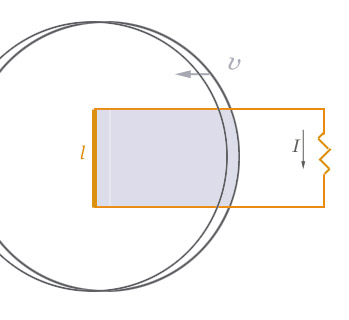 We could do a second experiment, where instead of moving the wire to the right, we keep the wire still and move the magnet to the left. Now there is no obvious Lorentz force: the charges in the wire have no velocity.
We could do a second experiment, where instead of moving the wire to the right, we keep the wire still and move the magnet to the left. Now there is no obvious Lorentz force: the charges in the wire have no velocity.
But this situation is related to the previous one by a low-speed ($v \ll c$) transformation, and so we suspect that the same voltage ought to appear, and experimentally it is found that it does! So, in this situation $${\cal E} = -\frac{d}{dt}\Phi.$$
Is the $emf$ really related to the flux and not the motion of the magnet or the wire loop? How could we check that?
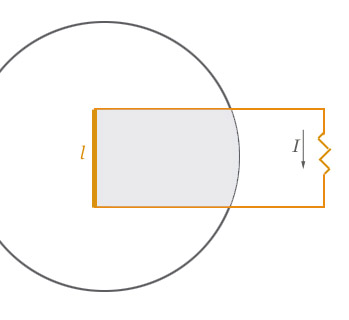 Now, in a third experiment, we try varying the flux in a different way. This time the magnet poles and the wire are kept still.
Now, in a third experiment, we try varying the flux in a different way. This time the magnet poles and the wire are kept still.
But the magnet turns out to be an electromagnet, so we can change the magnitude of the magnetic field while keeping everything else still.
[Experiment $\Rightarrow$] Again, a voltage appears. In this, as in the previous two cases, it turns out that the $emf$ is related to the change of the flux, by:
$${\cal E} = -\frac{d \Phi}{dt}.$$ This is Faraday's law.
The left-hand side of Faraday's law is $${\cal E}=\oint_C\myv E\cdot d\myv l=\int_S\myv\grad\times \myv E\,d\myv a$$ and the right hand side is $$-\frac{d\Phi}{dt}=-\frac{d}{dt}\int_S \myv B\,d\myv a = \int_S \left(-\frac{d}{dt}\myv B\right)\,d\myv a$$ So this implies...
$$\myv \grad\times \myv E=-\frac{d}{dt}\myv B$$ Maxwell's equation for $\myv \grad \times \myv E$.
Lenz's law
There is a right-hand rule to figure the change in flux. But an easier way to remember the sign is given by Lenz's law:
"In case of a change in a magnetic system, that change happens which tends to oppose the change."
So, for example, if you try to increase the flux through a loop of wire, currents will flow in the wire in such a way as to cause a magnetic field inside the loop in opposition to the direction of change of the flux.
[Jumping loop demonstration...]
Example: Problem 7.8
What's the flux through the square loop below?
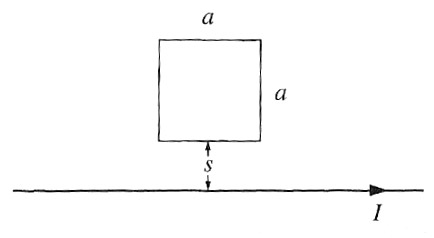
The field of a long (~infinite) wire is $B_{\phi} = \frac{\mu_0 I}{2 \pi s}$.
The flux in the loop (as a function of $s$) is... $$\begineq \Phi(s) &= \int_{\cal S} \myv B \cdot d\myv{a} = \int_0^{z=a} dz \int_s^{s+a} ds' \frac{\mu_0 I}{2 \pi s'}\\ &=\frac{\mu_0 I a}{2 \pi} [ln(s+a)-ln(s)]\\ \endeq$$
What's the generated $emf$ if the loop is pulled with speed $v$ away from the wire? $$ {\cal E} = -\frac{d}{dt}\Phi=...$$