Drude theory of conductivity
So, how does current flow in a wire happen at a microscopic level?
Ohm's law
Usually the speeds are slow enough (< 1mm/sec) that we can neglect the magnetic forces with very little error: $$\myv J = \sigma \myv E$$ This is the geometry-independent form of Ohm's law.
You are probably more
used to seeing it like this (assuming a uniform current density):
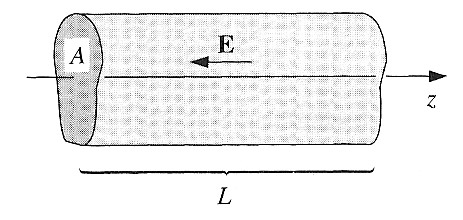
For a conductor that has a uniform cross-section $A$, and length $L$, if the electric field is uniform, then the current density is also uniform, and so... $$I=JA = \sigma EA.$$
The electric field is related to the electric potential at either end of the wire by: $$ "V" \equiv \Delta V = \int_{z=0}^{z=L} -\myv E \cdot d \myv \ell = EL.$$
Combining these... $$V= I \frac{L}{\sigma A} = IR.$$
or the more pedagogically appropriate form: $$I=V/R,$$ where $R=\frac{L}{\sigma A}$.
Uniform electric field?
Boundary conditions...
- At either end of the conductor, the potential is constant, and that means $\myv E$ is perpendicular to either end.
- Between the ends of the conductor, $\myv J = \sigma \myv E$ is parallel to the surface.
A uniform electric field is compatible with these boundary conditions, $\Rightarrow$ this must be the solution.
Microscopic theory of resistivity
With constant acceleration, $v=at$. It seems like current ought to increase linearly with time after turning on the electric field in a conducting wire. No? This is not what Ohm's law says...
Collisions
In wires, the electrons (charge carriers) are colliding with something in the system--perhaps..
- the positive ion cores (Drude)
- or crystal defects
- or "phonons"--lattice vibrations (modern QM).
If that's the case, let's re-calculate assuming:
- a mean free path $\lambda$--an electron moves an average distance $\lambda$ between collisions.
- electrons start at $v=0$ after each collision,
- the distance $\lambda$ is related to the average time between collisions by $\lambda=\frac{1}{2}at_\text{ave}^2$,
- that is, $t_\text{ave} = \sqrt{\frac{2\lambda}{a}}$,
- the average speed is $v_\text{ave} = \frac{1}{2}at_\text{ave} = \sqrt{\frac{\lambda a}{2}}.$
- Since $a \propto E$, we should expect that $I \propto v_\text{ave} \propto \sqrt{E}$.
We know empirically that $I \propto E$, So, hmmm, this theory doesn't quite work.
Drude theory
 Paul Drude (1863-1906) modified the picture above in two ways...
Paul Drude (1863-1906) modified the picture above in two ways...
- Let's assume that the electrons are in thermal equilibrium with the things they're colliding with: After a collision, the velocity is not zero, but rather $v_\text{thermal}$.
- It turns out $v_\text{thermal} \gg v_\text{drift}$, so
- The average time between collisions is not related to the acceleration, but is just $t_\text{ave} = \lambda/v_\text{thermal}$.
- So, the average (drift) velocity is $$v_\text{ave} = \frac{1}{2}a t_\text{ave}=\frac{1}{2}\frac{qE}{m}\frac{\lambda}{v_\text{thermal}}.$$
If $n$ is the number of molecules per unit volume, $f$ is the number of free electrons per molecule, $q$ is the carrier charge, and $m$ is the mass of the carrier, we have... $$\myv J = nfq \myv v_\text{ave}=\left(\frac{nf\lambda q^2}{2mv_\text{thermal}}\right) \myv E.$$ And the quantity in parentheses is apparently the conductivity.
This formula shows that Drude's theory correctly accounts for the linear relationship between $\myv J$ and $\myv E$.
As the temperature drops, $v_\text{thermal}$ drops, and so the resistivity $\rho=1/\sigma \propto v_\text{thermal}$ also drops. (See Ashcroft and Mermin, "Solid State Physics"). ...Yup!
In this picture, the time between collisions is mainly determined by the thermal velocity. The changes in velocity due to the acceleration in the electric field account for the average current in the direction of the field, but are small compared to the average velocity of the charge carriers.
The potential difference $V$ from one end of the conductor to the other is the work (energy) per unit charge to move charge through the circuit.
Multiply this energy per charge times the charge / second ($I$) moving through the circuit, we'll get a power (energy / time): $$P= VI = I^2 R,$$ which appears as resistive heating of the circuit.