The auxiliary field $\myv H$

In which we define a field out of $\myv B$ and $\myv M$: $$\myv H \equiv \frac{1}{\mu_0}\myv B - \myv M$$ similar to what we did with the electric displacement $\myv D$.

Magnetization gives rise to bound currents. Any other currents we'll call "free currents", $\myv J_f$. $$\myv J = \myv J_b + \myv J_f.$$

The magnetic field $\myv B$ does not care where the current comes from, but arises from both bound and free currents: $$\begineq\frac{1}{\mu_0} \myv \grad \times \myv B &= \myv J = \myv J_b + \myv J_{f} \\ &=\myv \grad \times \myv M + \myv J_f.\endeq$$

So, $$\Rightarrow \myv \grad \times(\frac{1}{\mu_0}\myv B - \myv M) = \myv J_f.$$

A new field $\myv H$: the auxiliary field: $$\myv H \equiv \frac{1}{\mu_0}\myv B - \myv M.$$

we have, $$\myv \grad \times \myv H = \myv J_f,$$

and there's an "Ampere's law" for free charge: $$\oint \myv H \cdot d \myv{l} = (I_f)_\text{enc}.$$

Magnetic field boundary conditions

Normal components

The vanishing divergence $\myv \grad \cdot \myv B=0$ can be written in integral form $$\oint \myv B \cdot d \myv a = 0.$$

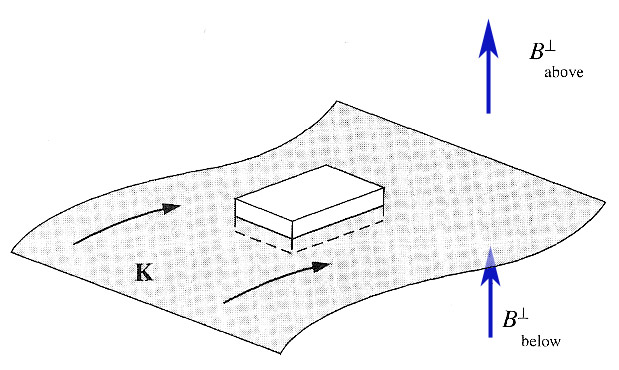
The 'pillbox' in the picture has a height which is small compared to its length and width. Applying the integral to this pillbox, apparently $$B_\perp^\text{above} - B_\perp^\text{below}=0.$$

Since the auxiliary field is $\myv H \equiv \frac{1}{\mu_0}\myv B - \myv M$, $$H_\perp^\text{above} - H_\perp^\text{below} =-( M_\perp^\text{above} - M_\perp^\text{below}).$$

Tangential components

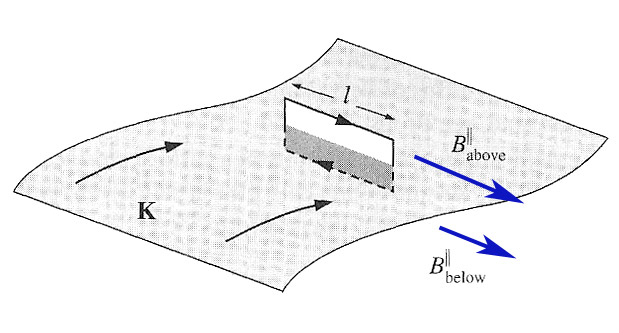
Apply Ampere's Law to a loop oriented perpendicular to a surface current $\myv K$: $$\oint \myv B \cdot d \myv{l} = B_{||}^\text{above} l - B_{||}^\text{below} l = \mu_0 I_\text{enc} = \mu_0 K l,$$

that is, $$B_{||}^\text{above} - B_{||}^\text{below} = \mu_0 K .$$

If the loop is parallel to the surface current, the field difference above is zero. Putting these two results together with the behavior of the perpendicular component, $$\myv B_{||}^\text{above} - \myv B_{||}^\text{below} = \mu_0\myv K \times\uv{n}.$$

Since the curl of $\myv H$ is the free current density... $$\myv H_{||}^\text{above} - \myv H_{||}^\text{below} = \myv K _{f} \times\uv{n}.$$

Magnetic vector potential

It can be shown that the magnetic vector potential is continuous across a boundary $$\myv A^\text{above} = \myv A^\text{below}.$$

But the normal derivative of the vector potential need not be continuous. $$\frac{\del \myv A^\text{above}}{\del n}- \frac{\del \myv A^\text{below}}{\del n}=-\mu_0\myv K.$$

Problem 6.15 - Uniformly magnetized sphere

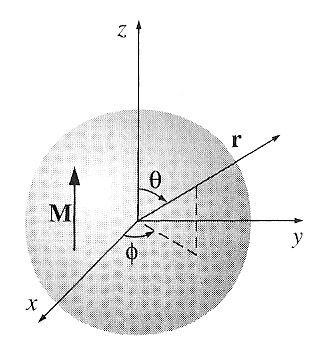Find the magnetic field inside and outside a uniformly magnetized sphere. (Here's the magnetic vector potential way to go after this problem.)

There is no free current in this problem: $\myv J_{f} = 0$. So $\myv \grad \times H=0$,

and this means that we can express $\myv H$ as the gradient of a scalar potential $W$: $$\myv H = - \myv \grad W.$$ What is $\myv \grad \cdot \myv H=\myv\grad\cdot(\myv B/\mu_0-\myv M)$?

  • $\myv\grad\cdot\myv B=0$, always.
  • The divergence of a constant is zero. So $\myv\grad\cdot\myv M=0$ both inside and outside the sphere. (Though the boundary is another matter).
  • $\Rightarrow \myv\grad\cdot\myv H =0$ everywhere except at the boundary.

Subbing in $\myv\grad W=-\myv H$ into the divergence above gives us... $$\myv \grad \cdot \myv \grad W = \grad^2 W = 0.$$ This is Laplace's equation, which apparently holds everywhere except for the surface of the sphere at $r=R$.

This new scalar potential is continuous across the surface. To see this, imagine that $b$ is a position just below the sphere's surface and $a$ is just above. According to the fundamental theorem for gradients, $$\begineq W(\myv a) - W(\myv b) &= \int_b^a (\myv \grad W)\cdot d\myv l = \int_b^a \myv H \cdot d\myv l \\ &= -\left. \int_b^a H_\perp d l \right|^{\text{as }(a-b) \to 0} \to 0.\endeq$$ As the path difference $(a-b)\to 0$, this will be small compared to the finite difference in $H_\perp$.

The solution to Laplace's equations for azimuthally symmetric conditions in spherical coordinates is: $$W=\sum_{l=0}^{\infty} \left(A_l r^l + B_l \frac{1}{r^{l+1}}\right)P_l(\cos \theta).$$

Continue the development in pairs and a triplet...



Now requiring that this potential should not blow up at $r=0$ nor as $r\to\infty$: $$W_\text{in}=\sum A_l r^l P_l(\cos \theta) \text{ for }r\lt R $$ $$ W_\text{out}=\sum B_l \frac{1}{r^{l+1}} P_l(\cos \theta) \text{ for }r\gt R$$

Let's apply our just-acquired boundary conditions at the surface of the sphere ($r=R$) that... $$H_\perp^\text{above} - H_\perp^\text{below} =-( M_\perp^\text{above} - M_\perp^\text{below}.$$

  • $\left.H_\perp^\text{above}\right|^{r=R}= -\left.\frac{\del}{\del r} W_\text{out}\right|^{r=R} -\sum B_l \frac{-(l+1)}{R^{l+2}}P_l(\cos \theta).$
  • $H_\perp^\text{below}]^{r=R}=-\frac{\del}{\del r} W_\text{in}]^{r=R}=-\sum A_l lR^{l-1}P_l(\cos \theta).$
  • $M_\perp^\text{above} = 0.$
  • $M_\perp^\text{below} = \myv M_r = (M_0\uv{z})_r = M_0 \cos \theta.$

So, at the surface of the sphere, we have: $$\sum_l \left(B_l \frac{(l+1)}{R^{l+2}}+A_l lR^{l-1}\right)P_l(\cos \theta)=M_0 \cos \theta.$$

Now, $\cos(\theta) = P_1(\cos(\theta))$, so apparently only the $l=1$ polynomial is needed, so $A_l=0=B_l$ unless $l=1$. The previous equation becomes: $$B_1 \frac{2}{R^3}+A_1 =M_0 .$$

Using the continuity of $W$ across the interface, we have: $$\left.W_\text{in}\right|^{r=R} = \left.W_\text{out}\right|^{r=R}$$ $$A_1R^1\cos(\theta)=\frac{B_1}{R^{2}\cos(\theta}$$ $$B_1=A_1 R^3$$

So, we can substitute $B_1$ into the previous equation getting $$ A_1R^3 \frac{2}{R^3} + A_1=M_0$$ $$\Rightarrow A_1 = M_0 /3$$

Sooooo, returning to our expression for the potential, $$W_\text{in}=A_1 r^1 P_1(\cos\theta) = \frac{M_0}{3}r\cos\theta=\frac{M_0}{3}z.$$

The auxiliary field is $$\myv H = -\myv\grad W=-\frac{M_0}{3}\myv \grad z = -\frac{M_0}{3}\uv{z},$$

where I've used the Cartesian form of the gradient $\myv \grad = \uv x \frac{\del}{\del x} +\uv{y}\frac{\del}{\del y}+\uv{z}\frac{\del}{\del z}.$

The field can be calculated from: $$\myv B = \mu_0(\myv H + \myv M) = \mu_0(-\frac{1}{3}M_0\uv{z} + M_0\uv{z})=\mu_0\frac{2}{3}M_0 \uv{z}.$$

What is the field outside?
$$\begineq W_\text{out}&=B_1\frac{1}{r^2}P_1(\cos\theta)\\ &=\frac{A_1 R^3 \cos\theta}{r^2}=\frac{M_0R^3\cos\theta}{3r^2}.\endeq$$

This is not as simple. But let's use the spherical-coordinate form of the gradient to find $\myv H$: $$\begineq \myv H &= -\myv \grad W=\uv{r} \frac{\del}{\del r} W-\uv{\theta} \frac{1}{r}\frac{\del}{\del \theta)}W\\ &=\frac{M_0R^3}{3}\left[\uv{r} \frac{2\cos \theta}{r^3}+\uv{\theta} \frac{1}{r}\frac{\sin \theta}{r^2}\right]\\ &=\frac{M_0R^3}{3r^3}\left[\uv{r} 2\cos \theta+\uv{\theta} \sin \theta\right].\endeq$$

Since the magnetization outside vanishes, $\myv M=0$, $$\begineq \myv B &= \mu_0 \myv H \\ &=\frac{\mu_0 M_0R^3}{3r^3}\left[ 2\cos \theta \,\uv r+\sin \theta\,\uv\theta\right].\endeq$$

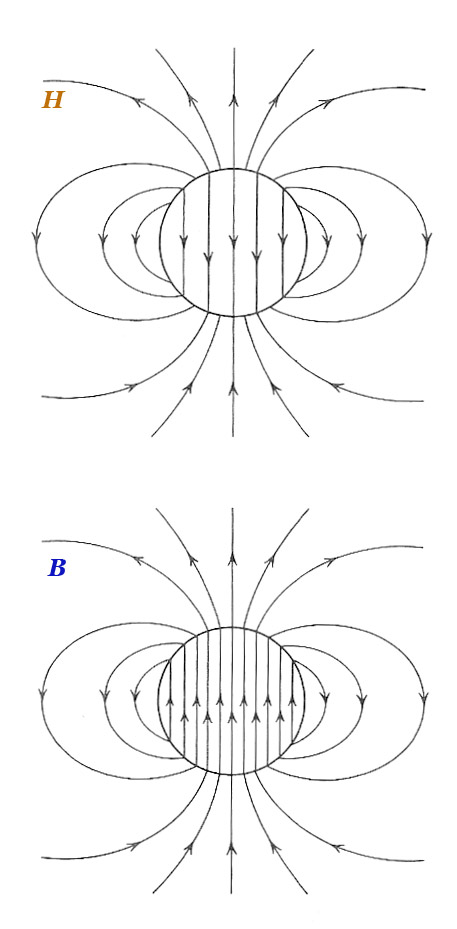Sketches