Magnetism
In electrostatics, we defined polarization,
$\myv P \equiv$ electric dipole moment per unit volume.
Now, Magnetization:
$\myv M \equiv$ magnetic dipole moment per unit volume.
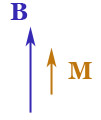
There are at least three different kinds of magnetic behavior of materials: ($M_B$ is the component of $\myv M$ that lies in the direction of an applied magnetic field $\myv B$.)
 $\frac
{d M_B}{d B} \gt 0$: para-magnetism,
$\frac
{d M_B}{d B} \gt 0$: para-magnetism,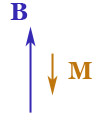 $\frac{d
M_B}{d B} \lt 0$: dia-magnetism, and
$\frac{d
M_B}{d B} \lt 0$: dia-magnetism, and $\myv M \neq 0$ even
when $\myv B=0$: ferro-magnetism.
$\myv M \neq 0$ even
when $\myv B=0$: ferro-magnetism.
Torques on a constant-current loop
So, let's calculate the torque in a magnetic field of one such rectangular loop:
The magnetic force on a line of current is: $$\myv F_m = \int dq\,\myv v\times\myv B=I \int d\myv l \times \myv B.$$
The loop shown is tilted by an angle $\theta$ from the $x$-$y$-plane. There is a magnetic field in the $\uv{z}$ direction, so $\myv B = B\uv{z}$.
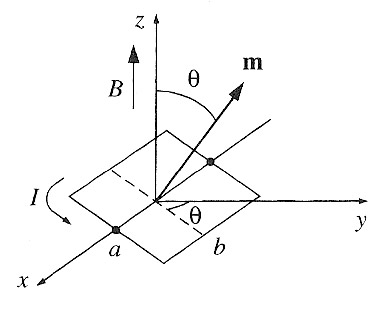
What's the sum of all the torques, $\myv \Gamma=\myv F \times \myv r$ acting on the current loop?
Here,- Calculate the total force on each the four current segments, and picture the force as acting at the center of each current segment.
- Add up the 4 torques about the origin $\myv \Gamma_i=\myv F_i\times \myv r_i$, where $\myv r_i$ is a vector from the origin with its tip at the center of each of the four current segments in turn.
What is the stable equilibrium position of the loop, when all the torques add up to zero? [and slight deviations from equilibrium will cause the loop to go back to the same position...]
Putting these together...
$$\myv \Gamma = Iab B \sin \theta\uv{x} = \myv m \times \myv B .$$
The net effect of this torque is a tendency for magnetic dipoles to line up with the magnetic field. This accounts for paramagnetism in a general way.
Why doesn't the current change instead of the tilt...?
What microscopic entity is this likely to apply to?
In real materials, because of the Pauli exclusion principle, every filled orbital will have just as many spin up as spin down electrons. This combination acts like something with no net magnetic dipole moment. So paramagnetism should only occur in materials that have an unpaired electron (materials with odd $Z$).
Mutual spin orientation
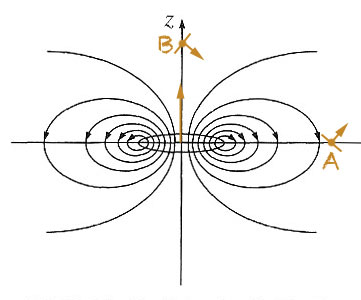 If the magnetic field is due to a current loop at the origin with a dipole-ish field, and we place a second small loop at ${\cal A}$ which is free to rotate, what orientation will the small dipole take on? What orientation would a small dipole at ${\cal B}$ take on?
If the magnetic field is due to a current loop at the origin with a dipole-ish field, and we place a second small loop at ${\cal A}$ which is free to rotate, what orientation will the small dipole take on? What orientation would a small dipole at ${\cal B}$ take on?
"Orbiting" charge
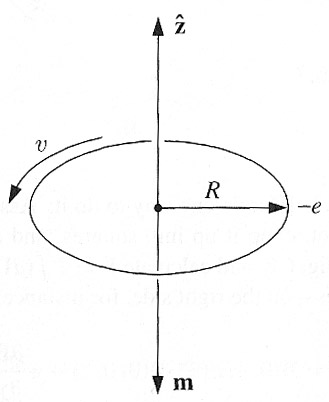 QM does not support the idea of an electron orbiting the nucleus like a planet about the sun.
QM does not support the idea of an electron orbiting the nucleus like a planet about the sun.
Still this classical picture can account qualitatively for diamagnetism:
- The electric force of the positive nucleus: $$\frac{e^2}{4\pi\epsilon_0 R^2} = m_e\frac{v^2}{R}.$$
- The hurtling electron looks like a current: $$I=\lambda v=\frac{ev}{2\pi R},$$
- with a dipole moment $m=I\pi R^2$: $$\myv m=-\frac{1}{2}evR \uv{z}.$$
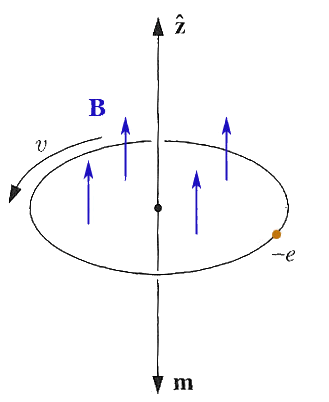 Now,
imagine that a magnetic field is turned on.
Now,
imagine that a magnetic field is turned on.
- What is the direction of the magnetic force on the electron?
- *If* the radius of the orbit is not allowed to change (Q for QM: why?) will the electron speed up or slow down?
- What is the direction of the *change* of the magnetic moment of this system?
This is apparently diamagnetism: Magnetization increases opposite to the magnetic field.
This affects both electrons (even if opposite spin orientation) in the same orbital angular momentum state. It is most prominent in materials with closed electron shells (that is, no spare electrons that are subject to paramagnetism).
Most materials (including frogs and grapes) are weakly diamagnetic.
Diamagnetism is a weak effect. If a material responds both diamagnetically and paramagnectically to some extent, its net behaviour is usual paramagnetic.
There is no diamagnetic effect for an isolated electron. Why?
We can't justify classically this business of assuming that the electron has to stay in an orbit at the same distance. Diamagnetism is ultimately a quantum phenomenon. But the behavior of this classical picture does agree with the empirical behavior of real (quantum) diamagnets.
Problem 6.6
Which would you expect to be diamagnetic or paramagnetic?: Al, Cu, CuCl2, C, Pb, N2, NaCl, Na (metal), sulfer, H2O ?