Magnetic vector potential and dipoles
- The magnetic vector potential $\myv A$: $$\myv B=\myv \grad\times \myv A$$
- Multipole expansion of field due to currents.
- Magnetic dipole.
- Examples (including a very strange result for the electron).
Vector potential
Narrated (~ 3 min).
Revisiting the Helmholtz theorem, it tells us that a vector field that has a curl: $$\myv \grad \times \myv B = \mu_0 \myv J,$$
but no divergence... $$\myv \grad \cdot \myv B = 0,$$
may be expressed as the curl of a vector function, that we'll call the magnetic vector potential $\myv A$, $$\myv B = \myv \grad \times \myv A.$$
Vector identity (11): $$\myv \grad \times \myv B=\myv \grad \times(\myv \grad \times \myv A) = \myv \grad (\myv \grad \cdot \myv A)-\grad^2\myv A=\mu_0 \myv J .$$
[With electric potentials, we can add a scalar to the potential, and the electric field $-\myv E = \myv \grad (V+k)=\myv \grad V$ remains unchanged.]
The curl of any gradient vanishes, $\myv \grad \times \myv \grad f=0$,
So we can add the gradient of any scalar function $\lambda(\myv r)$ to the magnetic potential, $ \myv \grad \times (\myv A + \myv \grad \lambda )=\myv \grad \times \myv A $. This property can be used to chose a scalar field $\lambda $ (choose the 'gauge') such that $$\myv \grad \cdot \myv A=0$$ (the "Coulomb gauge").
Then, Ampere's law -- $\myv\grad\times \myv B=-\mu_o \myv J$ -- can alternately be stated in terms of the potential... $$\grad^2\myv A = -\mu_0\myv J .$$
This is 3 Poisson equations (one for each Cartesian coordinate).
We'll use Helmholtz' constructed potential which is the one appropriate for the Coulomb gauge to find the potential by integrating the current density:
$$\myv A (\myv r) = \frac{\mu_0}{4 \pi} \int \frac{\myv J(\myv r')}{\rr} d \tau'$$
Multipole expansion of $\myv A.$
Narrated:Dipole moment (~9 minutes)
In electrostatics, when we had some localized charge distribution, we figured out...
- a general potential $V(\myv r),$
- far from the charge distribution,
- an expansion of $1/\rr$ in powers of $1/r.$
We can do the same for a localized current distribution.
We already did the heavy lifting with the multipole charge
distribution to
show....
$$\begineq \frac{1}{\rr} &= \frac{1}{r} \sum_n \frac{r'}{r}^n P_n(\cos \theta')\\
&=\frac{1}{r} + \frac{\myv r \cdot \myv r'}{r^3}+\frac{1}{2}\left(\frac{3(\myv r \cdot \myv r')^2}{r^5}-\frac{r'^2}{r^3}\right)+....\endeq$$
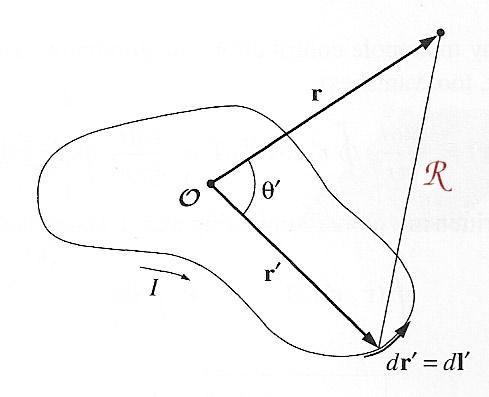 Consider some loop of current (pictured). What is the magnetic potential
far from the loop? Using our just discovered integral for the potential in
terms of the current ($I\,d\myv l$) instead of the current density ($\myv J\,d\tau$)...
$$\myv A (\myv r) = \frac{\mu_0}{4 \pi} \int \frac{ I(\myv r')}{\rr}
d \myv l'$$
Consider some loop of current (pictured). What is the magnetic potential
far from the loop? Using our just discovered integral for the potential in
terms of the current ($I\,d\myv l$) instead of the current density ($\myv J\,d\tau$)...
$$\myv A (\myv r) = \frac{\mu_0}{4 \pi} \int \frac{ I(\myv r')}{\rr}
d \myv l'$$
And subbing in the expression for $1/\rr$... $$\begineq \myv A(\myv r) &= \frac{\mu_0I}{4\pi} \left[\frac{1}{r}\oint d\myv l' + \frac{1}{r^2}\oint r' \cos \theta' d\myv l'\right.\\ &&\ \ \ \ \left. +\frac{1}{r^3}\oint r'^2\left(\frac{3}{2}\cos^2\theta'-\frac{1}{2}\right)d\myv l'+...\right].\endeq$$
The first term is the monopole term, then the dipole term, then the quadrupole, etc.
The monopole term vanishes (why??): $$\oint d\myv l' = 0.$$
So, usually the dominant term is...
The magnetic dipole
$$\myv A_\text{dip} =\frac{\mu_0I}{4\pi r^2}\oint r'\cos\theta' d\myv l'.$$Using a result from problem 1.61 it can be shown that...$$\oint r'\cos\theta' d\myv l' = \oint (\uv{r}\cdot \myv r')d\myv l' = -\uv{r} \times \int d\myv a'.$$where $\int d\myv a'$ is a surface integral over the surface bounded by the closed path of the line integral.
So, $$\myv A_\text{dip} =\frac{\mu_0}{4\pi} \frac{\myv m \times \uv r}{r^2},$$ where the magnetic dipole moment, $\myv m$, is: $$\myv m\equiv I\int d\myv a = I\myv a.$$ The integral, $\myv a$, is the 'vector area' of the loop. If the loop is flat the magnitude of the vector area is the same as the area inside the loop, and it points (right hand rule) perpendicular to the area.
Narrated: Magnetic field due to a dipole (~ 4 min)
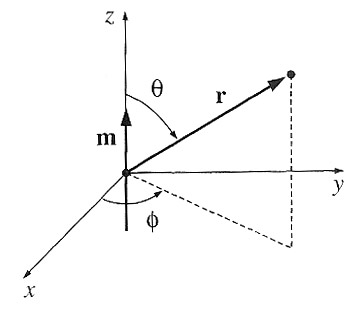 In spherical coordinates, if the magnetic dipole is pointing along the $z$-axis,
we can express the magnetic potential of the dipole as:
$$\myv A_\text{dip} =\frac{\mu_0}{4\pi}\frac{m\sin\theta}{r^2} \uv \phi .$$
In spherical coordinates, if the magnetic dipole is pointing along the $z$-axis,
we can express the magnetic potential of the dipole as:
$$\myv A_\text{dip} =\frac{\mu_0}{4\pi}\frac{m\sin\theta}{r^2} \uv \phi .$$
Then we figure the magnetic field using the expression for the curl in spherical coordinates: $$\begineq \myv B_\text{dip}(\myv r) &= \myv \grad \times \myv A_\text{dip} \endeq$$
$$=\frac{\mu_0 m}{4 \pi r^3}\left(2\cos \theta \,\uv{r} +\sin\theta\, \uv \theta\right).$$
Problem 5.37
A phonograph record of radius $R$, with a uniform surface charge $\sigma$, is rotating at constant angular velocity $\omega.$ Show that its magnetic dipole moment works out to $|\myv m|=\pi \sigma \omega R^4 / 4.$
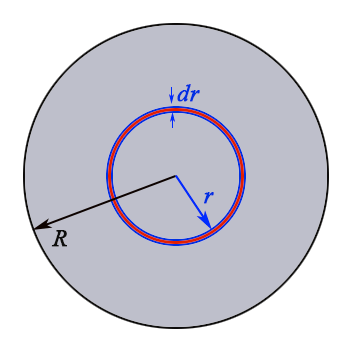 Divide the record into circular 'rings' of length $2\pi r$ and thickness $dr$.
Divide the record into circular 'rings' of length $2\pi r$ and thickness $dr$.
The area of one ring is $2\pi r\,dr$ and the charge in the (red) ring is $dq = \sigma 2\pi r\,dr$.
The charge, $dq$, in one ring rotating at $\omega$ radians/sec makes one full rotation ($2\pi$ radians) in a time $T=2\pi/\omega$. So the current moving past a fixed point on the ring is $dI =dq/T=\frac{\sigma 2\pi r\,dr}{2\pi/\omega}=\sigma r\omega \,dr$.
For one ring of current, its magnetic dipole moment $dm$ is the current times the enclosed area ($\pi r^2$): $$dm= dI\, a= dI\, \pi r^2 = \sigma \omega r \,dr\, \pi r^2=\sigma\pi\omega r^3\,dr.$$
So, the total magnetic dipole moment is $$m = \int dm = \int_0^R \sigma \omega \pi r^3 \,dr = \color{red}{\pi \sigma \omega R^4 / 4}.$$
The gyromagnetic ratio - Problem 5.58
 A thin uniform 'donut' or 'ring' with total charge $Q$ and mass $M$ rotates about its
axis. Find the ratio of its magnetic dipole moment to its angular momentum.
This is called its "gyromagnetic ratio", $g=\frac{|\myv m|}{|\myv L|}$.
A thin uniform 'donut' or 'ring' with total charge $Q$ and mass $M$ rotates about its
axis. Find the ratio of its magnetic dipole moment to its angular momentum.
This is called its "gyromagnetic ratio", $g=\frac{|\myv m|}{|\myv L|}$.
$\myv m = I \myv a$.
- $I=$Charge flowing past any point in the circuit per second.
- With $T=$ period of rotation (seconds / cycle) = $2\pi$ radians per cycle / $\omega$ radians / sec we have $$I=Q/T=\frac{Q}{(2\pi/\omega)}=\frac{Q\omega}{2\pi}$$
- $\myv a$ has magnitude $\pi R^2$ (and points in the $\uv z$ direction).
$\Rightarrow |\myv m|=Ia=\frac{Q\omega}{2\pi}\pi R^2= \frac{Q\omega R^2}{2}.$
$\myv L$, angular momentum $= \myv r \times \myv p$. For this ring of total mass $M$, $\myv L$ points in the $\uv z$ direction and its magnitude is
$|\myv L|=Mv\,R = M\omega R\,R=M\omega R^2.$
$g$--the ratio of dipole moment to angular momentum--the gyromagnetic factor--is
$g= \frac{|\myv m|}{|\myv L|} = \frac{Q \omega R^2}{2 M \omega R^2} = \frac{Q}{2M}.$
The surprising thing here is that $g$ is independent of $R$, the radius of the donut.
What is the gyromagnetic ratio for a sphere with a uniform charge density and mass density?
A sphere can be cut up into a bunch of donuts, of different radii. But all the donuts have the same angular momentum, $\omega$, and are rotating about the same axis $\uv z$.
- $g$ does not depend on the radius.
- As long as the sphere has a uniform charge- and mass-density, the ratio $Q/M$ (each is separately proportional to the volume of an individual donut) will be a constant for all donuts.
So, for a sphere (or, for that matter, any body of rotation), the ratio will be the same as for a single donut: $$g=\frac{|\myv m|}{L}=\frac{Q}{2M}.$$
What about the electron?
According to quantum mechanics, the electron has an unchanging angular momentum ("spin") of magnitude $L_e = \frac{1}{2}\hbar $.
The magnetic dipole moment of the electron is so special that it gets its own symbol: $$|\myv m_e| \equiv \mu_e.$$ (ahem, which differentiates it from $m_e$--the mass of the electron).
We know the charge, $-e$, and the mass, $m_e$ of the electron. So you'd kind of expect that the magnetic moment would be $$\begineq \mu_e&=gL=(\frac{q}{2M})L=\frac{-e}{2m_e} \cdot \frac{1}{2}\hbar = \color{red}{1}* \frac{-e \hbar }{4 m_e}\\ &= -\frac{(1.6\times10^{-19})(1.05 \times 10^{-34})}{4*9.11\times10^{-31}} \\ &= -4.61 \times 10^{-24}\text{A m}^2.\endeq$$
But experimentally, it is found that... $$\mu_e = (\color{red}{2.0023193043622} \pm 0.0000000000015) \frac{-e \hbar }{4 m_e}.$$
Hmmm...
- It doesn't work to picture the electron as a "rotating solid". The surface of the electron (with a typical estimate of the size of the electron) would need to be going faster than the speed of light.
- [As far as experiments can tell, it's terrifically "round" [spherically symmetric] down as far as we can measure.]
- Dirac's relativistic theory of quantum mechanics comes up with precise, integer value for the $g$-factor: $\mu_e=\color{red}{2}\left(\frac{-e\hbar}{4 m_e}\right)$.
- In Quantum Electro Dynamics (QED - elaborated by Feynmann, Schwinger, Tomonaga) charged particles interact with each other through an exchange of "virtual" photons.
- If you take into account
(QED) the interactions of an isolated electron with the virtual photons that it gives off, there is a slight correction to Dirac's result
which agrees exactly
(to within experimental uncertainty) with the measured value.
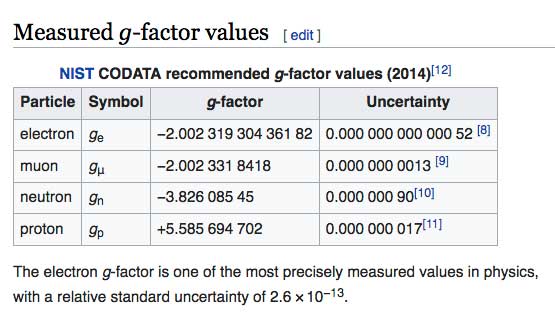
Wikipedia article on "g-factor".
The Bohr magneton, $\mu_B$ is this combination of constants: $$\mu_b=\frac{e\hbar}{2m_e}.$$
- Dirac was pretty darn right. His relativistic treatment of the electron the magnitude of the electron's magnetic moment was a big jump from the classical prediction of rotating solid body: ${\color{red}\frac 12}\mu_b \to {\color{red}1}\mu_b$.
- Feynmann and Schwinger got us fractionally closer still.