Magnetostatics - Biot-Savart
The source of magnetic fields is current flow.
We first considered electrostatics where stationary charges gave rise to stationary fields. The sources of electric fields are charges.
We should like to consider now stationary magnetic fields. These arise when the sources of the magnetic fields are stationary. What are those sources??
The sources of magnetic fields are currents.
Stationary currents means that the magnitudes and directions of all the kinds of current densities we've been considering are constant. There's one additional proviso: that there's no charge pileup ($\frac{\del \rho}{\del t}=0$), and as we've just seen the continuity equation, this means that... $$\myv \grad \cdot \myv J = 0.$$
When this is all true, the Biot-Savart Law allows us to calculate the magnetic field in the same way that Coulomb's Law let us calculate the electric field
--that is to say, ponderously, and with much integration:
$$\myv B(\myv r) = \frac{\mu_0}{4 \pi} \int \frac{\myv I \times \uv{\rr}}{\rr^2} dl' =\frac{\mu_0}{4
\pi} I \int \frac{d \myv l' \times \uv{\rr}}{\rr^2} .$$
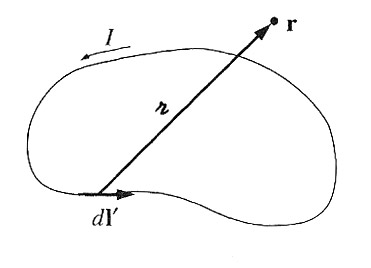
The constant $\mu_0$ is the permeability of free space, $$\mu_0 = 4\pi \times 10^{-7} N / A^2.$$
In this scheme, this results in the magnetic field being measured in units of tesla (T), where, 1 T = 1 N / (A $\cdot$ m) .
This should work out so that we get a force in N from the Lorentz force law.
Earth's magnetic field ~ $0.5 \times 10^{-4}$ T = 0.5 "gauss".
Strong lab magnet ~ 1 T.
Super conducting magnet ~ 20 T.
Field of a long straight wire
 We'd like to know the magnitude of the magnetic field around a very long (~
infinite) straight wire.
We'd like to know the magnitude of the magnetic field around a very long (~
infinite) straight wire.
Use our Biot-Savart equation... $$\myv B= \frac{\mu_0 I}{4 \pi}\int \frac{d\myv l' \times \uv\rr}{\rr^2}.$$
Consider a (rather artificial) current segment:

Convince yourself that, no matter what $\myv l$ is, $d\myv l \times \uv r$ is always a vector pointing in to the board ($-\uv z$ direction).
The magnitude of the integral above (substituting dy=dl) is then: $$\int_{-a}^{+a}\frac{ dy\, \sin(\phi)}{(x^2+y^2)}=\frac{2a}{x\sqrt{x^2+a^2}}.$$
Field at a distance $x$ from the center of a current-segment of length $2a$: $$B=\frac{\mu_0 I}{4\pi}\frac{2a}{x\sqrt{x^2+a^2}}=\frac{\mu_0 I}{2\pi x}\sin \theta_\text{max}$$where you have to remember how to come up with the direction...
Field at a distance $x$ from an infinitely long straight wire: Let $\theta_\text{max}\to 90^o$ in the expression above, then $$B=\frac{\mu_0 I}{2\pi x}$$
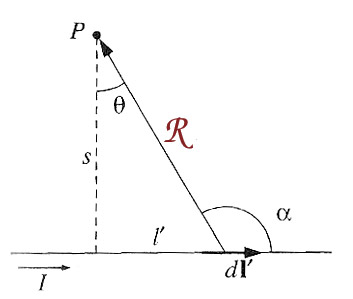
The cross product $d \myv l' \times \uv{\rr}$ is coming out of the page, and has a magnitude...
$$|d \myv l' \times \uv{\rr}| = dl' \sin \alpha = dl' \cos \theta$$
Differentiate $l'/s = \tan \theta \Rightarrow$ $$dl' =\frac{s}{\cos^2 \theta} d\theta.$$
Since $s=\rr \cos \theta$, $$\frac{1}{\rr^2} = \frac{\cos^2 \theta}{s^2}.$$
Force between two wires
 If two wires carrying currents $I_1$ and $I_2$ are a distance $d$ apart, what is the force per unit length between the two currents?
If two wires carrying currents $I_1$ and $I_2$ are a distance $d$ apart, what is the force per unit length between the two currents?
The field due to $I_1$ at the position of $I_2$ is pointing into the page, and has magnitude $$B = \frac{\mu_0 I_1}{2\pi d}$$
The magnetic force on $I_2$ is: $$ F = I_2 \int d \myv l \times \myv B = I_2 B \int d l .$$
So, the force per unit length is: $$ F/l = I_2 B = \frac{\mu_0 I_1 I_2}{2 \pi d}.$$