Linear dielectrics

Linear dielectrics: the polarization in an external field $\myv E$ obeys: $$\myv P = \alpha \myv E$$ Empirically, this is true for many materials as long as $|\myv E|$ is "not too large".

$$\myv P = \alpha \myv E\equiv \epsilon_0 \chi_e \myv E.\label{EP}$$

• $\chi_e$ is the electric susceptibility.
• $\chi_e$ is a dimensionless constant.
• We're still doing electrostatics, but we'd eventually find that $\chi_{e(\text{dynamic})}(\omega)$ is a function of oscillating field frequency, $\omega$, among other things.
• Materials that obey this are called linear dielectrics. Exceptions abound:
  1. This is a good approximation for non-big fields.
  2. Crystals often have slightly different susceptibilities in different directions.
  3. "Non-linear" materials are important (fiber optics...) and have higher-order terms, e.g. $\propto E^3$.

The electric displacement field in linear dielectrics can be written: $$\myv D \equiv \epsilon_0 \myv E + \myv P = \epsilon_0 \myv E + \epsilon_0 \chi_e \myv E = \epsilon \myv E,\label{ED}$$

where $$\epsilon \equiv \epsilon_0(1+\chi_e).$$

• $\epsilon$ is the permittivity of a material,
• $\epsilon_0$ is the permittivity of free space (of vacuum).

Another dimensionless constant that is frequently used is the relative permittivity, or ...

dielectric constant: $$K \equiv \frac{\epsilon}{\epsilon_0} = 1+ \chi_e.$$ Griffiths uses a less common notation describing $\epsilon_r$ as the relative permittivity, which is the same as the dielectric constant: $\epsilon_r\equiv K=\frac{\epsilon}{\epsilon_0}$.

Example: Free point charge in a dielectric medium

Imagine a "free" (that is, externally embedded) charge $+q$ at the origin in a dielectric medium that fills all (or at least, a lot of) space. What's the field?

By symmetry, $\myv E$, $\myv P$, and $\myv D$ have to be radial functions just of the radial distance to the charge. Applying Gauss' law, the displacement is related to the enclosed free charge by $$\int_{S}\myv D\cdot d\myv a = (q_f)_\text{enclosed}$$

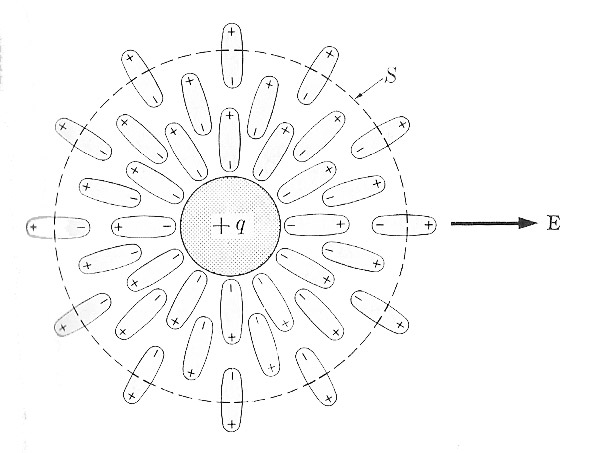
The electric field of the point charge is smaller than the vacuum field by a factor $1/K$.

Perhaps the accompanying picture makes this more plausible: At the distance shown from the origin, you can see that the effect of polarization is to leave an excess of negative charge in the volume enclosed by the sphere along with the positive free charge, thus reducing the overall amount of enclosed charge.

Capacitance and dielectrics

Imagine that a flat-plate capacitor with charge density $\pm \sigma$ (that is, a free charge density) on either plate has a dielectric material between the plates. The displacement field between the plates is constant, then $\myv \grad \cdot \myv D = \rho_f$ tells us that in the space between the plates, $$D_z = \sigma = \epsilon E_z=K\epsilon_0 E_z.$$

The electric field between the plates is reduced from its vacuum value by $1/K$. The potential difference between the plates, which is the line integral of $\myv E$ on a path from one plate to the other is also reduced by the same factor. The capacitance $$C=Q/V = KC_{\text{vac}},$$ is greater than it would be with nothing between the plates.

One way of writing the energy of a charged capacitor was $$W = \frac{1}{2}CV^2.$$

With the greater capacitance, it seems like this should also be increased by a factor $K$ compared to the vacuum-filled value. Is this still in agreement with our formula for energy in terms of the electric field amplitude? $$\frac{\epsilon_0}{2}\int E^2 d \tau = \frac{\epsilon_0}{2}*A*d*(E_z)^2.$$

With the dielectric in place, $E_z = \sigma / \epsilon=\frac{Q}{A \epsilon}= \frac{CV}{A \epsilon} $ and $d*E_z = V$, so, $$\begineq\frac{\epsilon_0}{2}\int E^2 d \tau &=\frac{\epsilon_0}{2}\int \frac{CV}{A \epsilon} \frac Vd d \tau = \frac{\epsilon_0CV^2}{2\epsilon Ad}\int d \tau = \frac{\epsilon_0CV^2}{2\epsilon Ad}Ad\\ &= \frac{\epsilon_0}{2 \epsilon }CV^2 = \frac{1}{K}\frac{1}{2}CV^2. \endeq$$

No, it's not in agreement. So perhaps we should reexamine how to calculate (in terms of the fields) the...

Energy around dielectrics

Let's re-calculate the energy, as it relates to the fields, in terms of bringing chunks of free charge in from infinity, one chunk $\Delta \rho_f$ at a time. The work done on one chunk will be: $$\Delta W = \int_\text{all space } (\Delta \rho_f)V \,d \tau = \int (\myv \grad \cdot \Delta \myv D) V \,d \tau.$$

Using product rule #5, $\myv\grad \cdot[V \Delta \myv D] = V \myv\grad \cdot\Delta \myv D + \Delta \myv D\cdot(\myv\grad V)$ : $$\begineq \Delta W &= \int \myv\grad \cdot[V \Delta \myv D] d \tau - \int \Delta \myv D\cdot \myv\grad V\, d \tau\\ &= \int \myv\grad \cdot[V \Delta \myv D] d \tau + \int \Delta \myv D\cdot\myv E\, d \tau.\endeq$$

Using the divergence theorem, we can re-write the first term as a surface integral at $r \to \infty$ where $V$ vanishes, so we have: $$\Delta W = \int \Delta \myv D\cdot\myv E \, d \tau.$$

For linear dielectrics, $\Delta \myv D = \epsilon \myv{\Delta E}$. Then, we also note that, for small changes (differentials) $\Delta(E^2) = \Delta(\myv E \cdot \myv E)= 2 \Delta \myv E\cdot\myv E$. Putting this together... $$\Delta W = \Delta\left(\frac{1}{2}\int \myv D \cdot \myv E\, d \tau\right).$$

So

$$W = \frac{1}{2}\int \myv D \cdot \myv E d \tau.$$

For a linear dielectric between the plates of a capacitor, $D=K\epsilon_0 E$ so the energy density would be $K*\epsilon_0 E^2/2$: a factor $K$ larger than if we had the same electric field in a vacuum.

The reason that the energy density is greater is that this way of calculating the energy automatically takes into account the energy needed to stretch the springs or twist molecules to get a dipole density in the material. [Griffiths covers this in a bit more detail in 4.4.3]

If you bring in a certain amount of free charge necessary to get a field $\myv E$ in the capacitor in vacuum, then if you replace the vacuum with a dielectric, the charges will polarize in such a way as to reduce the electric field, and you'll have to bring in *more* free charge to get the electric field up to the value it had in vacuum.

Force on a dielectric slab

Consider a parallel plate capacitor filled with material that has a dielectric constant $K$. For a particular charge $Q$ on the capacitor, the energy is.. $$W=\frac{1}{2}\int \myv E \cdot \myv D\, d \tau.$$

The displacement field inside the dielectric between plates of capacitor is related to the charge density on the capacitor plate $D=\sigma=K \epsilon_0 E$. So for all capacitors of the same size, with the same free charge density on the plates, the energy as a function of dielectric constant is $$\begineq W&=\frac{1}{2}\int \myv E \cdot \myv D\, d \tau =\frac{1}{2K \epsilon_0}\int D^2 d \tau \\ &= \frac{1}{2K\epsilon_0}\sigma^2 d\cdot l\cdot w .\endeq$$ This energy is clearly lower than the vacuum-filled energy--by a factor of $1/K$--if any dielectric material fills the gap.

Q: What?! Lower energy with a dielectric in place? I thought we just showed that the energy density was *higher* with a dielectric than without?

A: Before we were comparing the energy for a given electric field, with and without a dielectric present. In fact, we found that you have to add more charge to the plates when a dielectric is present to get the electric field up to the same value it had with a vacuum.

Now we're talking about putting a fixed amount of charge (free charge) on the capacitor plates and then comparing energies with and without the dielectric present.

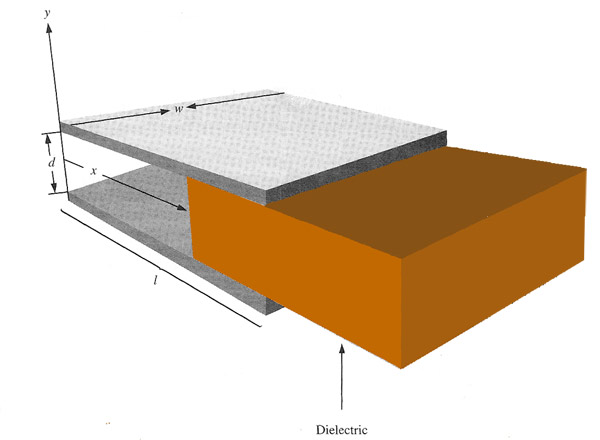
So, we'd expect in a general way that a slab of dielectric material would be drawn in to the gap of a capacitor. (One disconnected from a battery--so that the charge on the plates is constant.) The force drawing it in should be related to the change in energy of the system by $$\begineq F &= - \frac{d W}{d x} = - \frac{ d}{dx} \frac{1}{2}Q^2 / C \\ &= \frac{1}{2}\frac{Q^2}{C^2} \frac{dC}{dx}=\frac{1}{2}V^2 \frac{dC}{dx}.\endeq$$

For a parallel plate capacitor of width $w$, separation $d$, and length $\Delta x$, the capacitance is: $$C=Q/V = \frac{\sigma \cdot (w \Delta x)}{E d} = \frac{ \sigma \cdot (w \Delta x)}{\frac{\sigma}{K \epsilon_0} d}= \frac{K \epsilon_0 w \Delta x}{d}.$$

The difference in capacitance between a capacitor filled with material of dielectric constant $K$, and vacuum (air) is: $$\Delta C = \frac{\epsilon_0 w \Delta x}{d}(K-1)= \frac{\epsilon_0 w \Delta x}{d}((1-\chi_e)-1)=\frac{\epsilon_0 w \Delta x \chi_e}{d}.$$

Using the ratio $\frac{\Delta C}{\Delta x}$ as our rate of change of capacitance per unit length of inserted dielectric, the force works out as $$F = -\frac{\epsilon_0 \chi_e w}{2d}V^2.$$

 

Exam and homework review in comments...

image credit

Gallego