Electric potential
- Calculating the potential from $\myv E(\myv r)$.
- Calculating the potential from the charge density $\rho(\myv r)$.
Helmholtz' theorem assures us that an irrotational field, like $\myv E$, can be derived from a scalar potential $\myv E = -\myv \grad V(\myv r)$.
He also tells us how to contruct $V$: $$V(\myv r) = \frac{1}{4\pi} \iiint_\text{all space} \frac{\myv \grad ' \cdot \myv E(\myv r ')}{\rr} d \tau '=\frac{1}{4\pi\epsilon_0} \iiint_\text{all space} \frac{\rho(\myv r')}{\rr} d \tau'.$$ since $\myv\grad'\cdot\myv E(\myv r')=\rho(\myv r')/\epsilon_0$.
Great. But what if we only know $\myv E$ over a limited portion of space?? and not $\rho$??
The fundamental theorem for gradients
assures us that... $$\int_{\myv a}^{\myv b} (\myv \grad V) \cdot d \myv l = V(\myv b)-V(\myv a).$$
It's worth meditating on this notation just a bit: The integral $\int_\myv{a}^\myv{b}$ means the path integral from $\myv a$ to $\myv b$.
But don't we have to specify which path, ${\cal P}$, we want to follow?
In this special case, that the vector field to be integrated ($\myv \grad V=\myv E$) is the gradient of a scalar "potential function", the integral from $\myv a$ to $\myv b$ is path independent, and only depends one the end points of integration. So, yes, the integral from $\myv a$ to $\myv b$ is a path integral, taken along some particular path. But any path will give the same result, and therefore a path need not be specified.
On the other hand, since $\myv E = -\myv \grad V$, $$\begineq\int_{\myv a}^{\myv b} (\myv \grad V) \cdot d \myv l &= \int_{\myv a}^{\myv b} (-\myv E)\cdot d \myv l \\ &= \int_{\cal O}^{\myv b} (-\myv E)\cdot d \myv l - \int_{\cal O}^{\myv a} (-\myv E)\cdot d \myv l.\endeq$$
So, it looks like we could take any reference point ${\cal O}$, and calculate the potential from:
$$V(\myv r) = -\int_{\cal O}^{\myv r} \myv E\cdot d \myv l.$$
Units: Since $\myv E$ has units of $N / C$, the potential has units of $(N\cdot m)/C$ which is called a volt. Or, since a $N\cdot m$ is a joule, we could also say that a volt is a joule/coulomb.
The electric potential does not have units of energy, so the electric potential is not potential energy.
The force on a test charge $q$ is $\myv F=q\myv E$. So $\myv F\cdot d\myv l=dW$, that is d(Work). So integrating the work gives an energy, the change in the potential energy, $U_{\text{electric}}$, of our test particle, which is apparently $qV$.
Notice: $\myv E = \frac{\myv F}{q}$, and $V=\frac{U_\text{el}}{q}$.
Which reference point?
Changing the reference point from ${\cal O}$ to ${\cal O}'$ just adds a constant to the potential that we come up with... $$\begineq V'(\myv r) &= -\int_{\cal O'}^{\myv r} \myv E\cdot d \myv l=-\int_{\cal O'}^{\cal O} \myv E\cdot d \myv l+ -\int_{\cal O}^{\myv r} \myv E\cdot d \myv l\\ &= -\int_{\cal O'}^{\cal O} \myv E\cdot d \myv l + V(\myv r).\endeq$$
Really, what we care about is taking the gradient to find the electric field, and since the gradient of a constant is zero, $$\myv \grad V(r) = \myv \grad V'(r).$$
So let's agree on one. We'll pick the far edge of the universe...
${\cal O}$ at $\infty$, such that $V(\infty)=0.$
Problem 2.21
Find the potential inside and outside a sphere centered on the origin, of radius $R$, with a uniform charge density, such that its total charge is $q$.
You found the field for such a sphere in problem 2.12:
$$\myv E = \begin{cases}
\frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\uv{r} &
{\text{when}}\ r \gt R\\
\frac{1}{4\pi
\epsilon_0 }\frac{qr}{R^3} \uv{r} & {\text{ when} }\ r \lt R
\end{cases}
$$
$E_r$
$r$
The potential outside the sphere ought to be spherically symmetric--that is, $V(\myv r)=V(r)$, since the electric field is spherically symmetric.
Consider integrating along a line that goes through the origin, at any constant $\theta$ and $\phi$. Starting at $\infty$ and coming in to a distance $r$ from the origin, which is still outside the sphere... $$V(r) = - \int_\infty^r \myv E \cdot d \myv l'.$$
Now we can express the potential in terms of an integral of $r'$: $$\begineq V(r)-V(\infty)=V(r)-0 &= - \int_\infty^r \frac{1}{4\pi \epsilon_0}\frac{q}{r'^2} dr'\\ V(r)&= \frac{1}{4\pi \epsilon_0}\left.\frac{q}{r'}\right|_\infty^r=\color{blue}{\frac{1}{4\pi \epsilon_0}\frac{q}{r}}.\endeq$$
This is the potential outside ($\color{blue}{r \gt R}$) the sphere. Right at the surface of the sphere, the potential is $V(R)=\frac{q}{4\pi\epsilon_0 R}.$
The change in $V$ from the surface to a position $r$ inside the sphere (that is, $\color{red}{ r \lt R}$) is: $$\begineq V(r)-V(R) &= - \int_R^r \frac{q}{4\pi \epsilon_0 R^3}r' dr' \\ V(r)-\frac{q}{4\pi\epsilon_0R}&= \frac{q}{4\pi \epsilon_0 R^3} \left.\frac{r'^2}{2} \right|_R^r =\frac{q}{4\pi \epsilon_0}\left[-\frac{r^2}{2R^3}+\frac{R^2}{2R^3}\right]\\ \Rightarrow V(r) &=\color{red}{-\frac{q}{4\pi \epsilon_0}\frac{1}{2}\left[ \frac{3}{R}- \frac{r^2}{R^3}\right]}.\endeq$$
Graphing this...
$V(r)$
$r$
Potential of a collection of charge
Gee, wouldn't it be nice if we could calculate $\myv E$ by taking the gradient of our scalar potential $V$, instead of doing vector integrals over the charge density? Well, if only we could get the potential based on our charge distribution, that might be possible. Let's see how...
Superposition
The electric field obeys superposition. So, if we want the potential for a collection of charges, we could integrate $\myv E = \myv E_1 + \myv E_2+...$ as follows: $$\begineq V(\myv r) &= -\int_\infty^{\myv r} \myv E_\text{total}\cdot d\myv{l}'= -\int_\infty^{\myv r} (\myv E_1+\myv E_2+...)\cdot d\myv{l}' \\ &=-\int_\infty^{\myv r} \myv E_1\cdot d\myv{l}' -\int_\infty^{\myv r} \myv E_2\cdot d\myv{l}'+...\\ &=V_1(\myv r)+V_2(\myv r)+... \endeq$$
$\Rightarrow$ So, the potential also obeys a principle of superposition.
Potential of a point charge
The potential of a single point charge at the origin is... $$\begineq V(\myv r) &= -\frac{1}{4\pi \epsilon_0} \int_\infty^r \frac{q}{r'^2} dr' =\frac{1}{4\pi \epsilon_0}\left.\frac{q}{r'}\right|_\infty^r\\ &= \frac{1}{4\pi \epsilon_0}\frac{q}{r}.\endeq$$
Usually we find a charge not at the origin, but at some position $\myv r'$, in which case the potential just depends on the distance $\rr$ away from the charge. $$V(\myv r) = \frac{1}{4\pi \epsilon_0}\frac{q}{\rr}.$$
Since the potential obeys superposition, the potential for several point charges is... $$V(\myv r) = \frac{1}{4\pi \epsilon_0}\sum_{i=1}\frac{q_i}{\rr_i}.$$
It is a small step to the potential based on a continuous distribution of charge:
$$V(\myv r) = \frac{1}{4\pi \epsilon_0}\int \frac{\rho(\myv r')}{\rr} d \tau'.$$
Indeed, the Helmholtz theorem suggested that we could construct the scalar potential as... $$V(\myv r) \equiv \frac{1}{4\pi} \int \frac{D(\myv r ')}{\rr} d \tau ',$$ Where the divergence of our electric field: $D = \myv \grad \cdot \myv E=\rho/\epsilon_0$. So, there ya' go.
This is already an improvement on our integral expression for the electric field which involved keeping track of the vector components of $\uv \rr.$
Notice that positive charge corresponds to "hills" in the potential, and negative charge to "valleys".
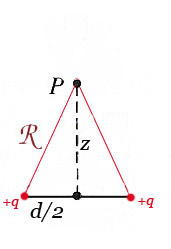
Problem 2.25
What's the potential at a height $z$ above the two charges separated by a distance $d$? Use this to calculate the force as the gradient of the potential.
 Notice
how much simpler the diagram is to calculate the potential compared to problem
2.2 ??!!
Notice
how much simpler the diagram is to calculate the potential compared to problem
2.2 ??!!
The potential is just the sum of the two single-particle potentials: $$V(z) = \frac{1}{4\pi \epsilon_0}[q/\rr + q/\rr]=\frac{1}{4\pi \epsilon_0}\frac{2q}{\sqrt{z^2+(d/2)^2}}.$$
Now, to get the electric field we use $\myv E = -\myv \grad V$. But we can still use symmetry to tell us the force has to be in $z$-direction. So, we *know* the gradient points in the $z$-direction. We only need to look at the $z$ component of the electric field,
$$\begineq E_z &= -\frac{\del}{\del z} V=-\frac{1}{4\pi \epsilon_0}2q\frac{\del}{\del z}\left(z^2+(d/2)^2\right)^{-1/2}\\ &=-\frac{1}{4\pi \epsilon_0}2q(-1/2)\left(z^2+(d/2)^2\right)^{-3/2}\frac{\del}{\del z}\left(z^2+(d/2)^2\right)\\ &=-\frac{1}{4\pi \epsilon_0}\frac{2qz}{(z^2+(d/2)^2)^{3/2}}.\endeq$$
Result is: $$E_z = +\frac{1}{4\pi \epsilon_0}\frac{2qz}{(z^2+(d/2)^2)^(3/2)}.$$