$\myv \grad \times \myv E$
...in which we find that the curl of the electric field is zero, everywhere! Other ways of stating this:
- $\myv \grad \times \myv E=0$.
- $\myv E$ is irrotational.
A single point charge
The field of a single point charge, $q$, at the origin is $$\myv E = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2}\uv{r}.$$ It turns out to be surprisingly easy to show that the curl (using spherical coordinates) of this field vanishes:
Calculating $\myv \grad \times \myv E$ in spherical coordinates for a single point charge at the origin. (It comes out to 0).
We can show this another way as well: Stoke's theorem applies to any vector field, including $\myv E$: $$\int_{\cal S} \myv \grad \times \myv E\cdot d \myv a = \oint_{\cal P} \myv E\cdot d\myv{l}.$$ This suggests that if $\myv \grad \times \myv E=0$ everywhere (including all the points on an arbitrary surface ${\cal S}$), then the line integral around the path ${\cal P}$ (and by extension *any* closed path we choose) must also vanish. Let's show that all closed paths give the same line integral of 0:
Here is a two-d slice through the origin, depicting schematically the field of the charge,
$$\myv E = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2}\uv{r},$$
and a path connecting two points $a$ and point $b$. (Nothing in what follows requires the $a$ and $b$ and the origin are all in the same plane. They can be anywhere in 3 dimensions.)
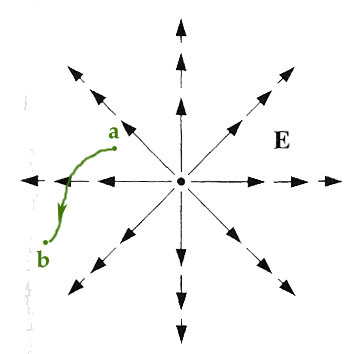
[Grapically, you can check for curl by placing your imaginary paddle wheel in the picture to look for an imbalance of flow on either side...]
The path integral from some point $\myv a$ to another $\myv b$ is $$\int_a^b \myv E \cdot d\myv{l}.$$
A step, $d\myv l$, along our path can be decomposed into components:
$d\myv{l} = dr\,\uv{r} + r \,d \theta \,\uv\theta + r \sin \theta\, d\phi \,\uv\phi$.
But the field of our charge at the origin has only a radial component, so
$$\myv E \cdot d\myv{l} = |\myv E|\uv r\cdot d\myv l = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2} dr$$
The path integral depends only on the radial component as you step along, and the integral is...
$$\begineq\int_{ a}^{ b} \myv E \cdot d\myv{l} &= \frac{1}{4 \pi \epsilon_0} \int_{ a}^{ b} \frac{q}{r^2} dr= \left.\frac{-1}{4 \pi \epsilon_0}\frac{q}{r}\right|_{r_a}^{r_b}\\ &=\frac{1}{4 \pi \epsilon_0}\left(\frac{q}{r_b}-\frac{q}{r_a}\right).\endeq$$
Oh!-- so it only depends on the radial coordinate of the initial and final position.
No details of the particular path taken from $a$ to $b$ were needed. So I could take a completely different path to get back from $b$ to $a$, and find $$\int_b^a\myv E\cdot d\myv l= \frac{1}{4 \pi \epsilon_0}\left(\frac{q}{r_a}-\frac{q}{r_b}\right).$$
Adding the results of the integral from $a\to b$ along an arbitrary path, and the integral from $b\to a$ along a different arbitrary path, gives zero, no matter what points $a$ and $b$ are taken. So we can conclude quite generally that $$\oint_\text{any path}\myv E\cdot d\myv l=0.$$
- [This might remind you of the work done as you move an object of mass 'm'
between two points in a gravitational field: The work only depends on the
height of the initial and final positions, and not the details of the path
taken. And if you return the object to its starting point, no net work will have been done.]
Generalizing to an arbitrary distribution of point charges
This calculaton was for a point charge at the origin. But if we translate the point charge and the path to some other location, the physics should be the same. So this result should hold no matter where the single charge or the path are!
Because of superposition, we could take the field of many particles apart into the fields of each point charge... $$\myv E_\text{net} = \myv E_1 + \myv E_2 +....$$
Since the path integral of the field due to any one charge vanishes, the sum should also vanish, so...
the path integral vanishes for any configuration of charges as well:$$\oint \myv E_\text{net} \cdot d \myv l = 0.$$
So, using Stokes' theorem once more: $$\int_{\cal S} \myv \grad \times \myv E\cdot d \myv a = \oint_{\cal P} \myv E\cdot d\myv{l}.$$ If the path dependent integral on the right vanishes for:
- Any path,
- single charges anywhere (not just at the origin),
- by superposition, for multiple charges as well,
Then it must also be true that the integral on the left vanishes under the same conditions. So we conclude that $\myv \grad \times \myv E = 0$ and at any location, no matter what the charge distribution is.
[You did or shortly will do problem 1.62 in which you showed that $\myv \grad \times(r^n\uv{r}) = 0$, and using that, you could also demonstrate this directly from our expression for the electric field.]
Summary
$$ \myv \grad \cdot \myv E = \frac{\rho}{\epsilon_0}$$
$$ \myv \grad \times \myv E = 0$$