$\myv \grad \cdot \myv E$
The divergence of the electric field is:
$$\begineq \myv \grad \cdot \myv E&=\left[\uv x \frac{\del}{\del x} +\uv y \frac{\del}{\del y}+\uv z \frac{\del}{\del z}\right] \cdot \left(E_x,E_y,E_z\right)\\
&=\frac{\del E_x}{\del x}+\frac{\del E_y}{\del y}+\frac{\del E_z}{\del z}
\endeq
$$
Gauss'/Gauss's Law
Remember Gauss' theorem? Writing that 'fundamental law for divergence' out with $\myv E$ as the vector field:
$$\oint_{\cal S} \myv E \cdot d \myv a = \int_{\cal V} \myv \grad \cdot \myv E \,d \tau.$$
The interpretation was that the flow out of a closed surface was equal to the sum over the enclosed volume of all the "sources" of flow enclosed by the surface.
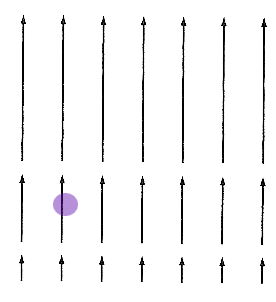
Thinking about the flow in 2 dimensions, the integral of the divergence inside the purple circle should be equal to the flow crossing the "surface" (perimeter) bounding the purple circle...

This would also mean that if there are no sources or sinks inside a surface, then the total flux through the surface is zero, i.e. "Just as much flow is coming out as what's going in".
Since charges are the sources (or sinks) of our electric field lines, this analogy suggests that the total flux of electric field through a closed surface is equal to the charge enclosed by the surface.

Let's show this is so:
The electric field from a very general charge distribution was:
$$\myv E(\myv r) = \frac{1}{4\pi \epsilon_0}\int_{\cal V} \frac{\rho(\myv{r}')}{\rr^2} \uv \rr\, d \tau'.$$
Using this in Gauss' theorem...
[Note that $\myv \grad \cdot$ is a derivative with respect to $\myv r$, not $\myv r'$.] $$\begineq \oint_{\cal S} \myv E \cdot d \myv a &= \int_{\cal V} (\myv \grad \cdot \myv E) d \tau\\ &=\int_{\cal V} \myv \grad \cdot \frac{1}{4\pi \epsilon_0}\int_{\cal V'} \frac{\rho(\myv{r}')}{\rr^2} \uv \rr\, d \tau' d \tau \\ &= \frac{1}{4\pi \epsilon_0} \int_{\cal V} \int_{\cal V'} \myv \grad \cdot \left[\frac{\myv \rr}{\rr^3} \right] \rho(\myv{r}')d \tau'\, d \tau.\\ &= \frac{1}{4\pi \epsilon_0} \int_{\cal V} \int_{\cal V'} \myv \grad \cdot \left[\frac{\myv r-\myv r'}{|\myv r-\myv r'|^3} \right] \rho(\myv{r}')d \tau'\, d \tau.\\ &= \frac{1}{4\pi \epsilon_0} \int_{\cal V} \int_{\cal V'} 4 \pi \delta^3 (\myv r - \myv r') \rho(\myv{r}')\,d \tau'\, d \tau\\ &= \frac{1}{4\pi \epsilon_0} \int_{\cal V} 4 \pi \rho(\myv{r}) d \tau\\ &= \frac{1}{\epsilon_0} \int_{\cal V} \rho(\myv{r}) d \tau=q_{\text enc}/\epsilon_0.\endeq$$
There are two very important results here...
- Divergence of $\myv E$--Referring back to first and last lines: $$\myv \grad \cdot \myv E = \frac{\rho}{\epsilon_0},$$ at each and every point in space.
- Gauss' Law -- that the surface integral of the electric field flux is equal to the total enclosed charge inside the surface: $$\oint_{\cal S} \myv E \cdot d \myv a = \oint_{\cal S}d\Phi_E = q_{\text enc}/\epsilon_0.$$