Curvilinear coordinates
Can you imagine talking about positions on Earth's surface in Cartesian coordinates? Non-cartesian coordinates (like spherical polar coordinates) sure are swell.
But, how do you do things like write a gradient or divergence, or do a volume integral??
Spherical polar coordinates
The position vector, $\myv r$, connecting the origin to a point $P$:
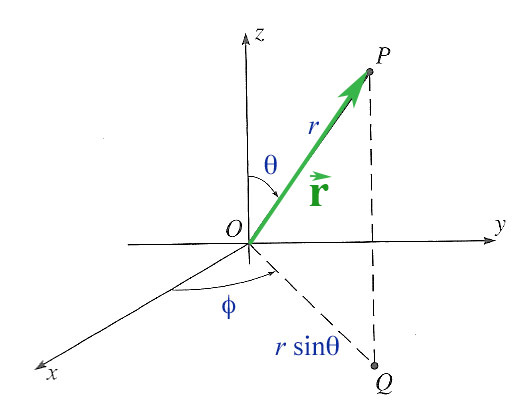
For positions $P$ on the surface of Earth, and with the origin at the center of Earth...
- $r$ would be constant, would be the Earth's radius,
- $\phi$ would be the longitude relative to the prime meridian, and
- $\theta$ would be (in the Northern hemisphere) 90 deg minus the latitude.
[Warning--Calculus books and some mathematicians prefer to swap the meaning of $\theta$ and $\phi$. But Mathematica uses the same convention that we use.]
Convince yourself of these conversions:
- $z= r \cos \theta$,
- [$OQ = r\sin \theta$]
- $x = OQ \cos \phi=r \sin \theta \cos \phi$,
- $y= OQ \sin \phi = r \sin \theta \sin \phi$
Unit vectors
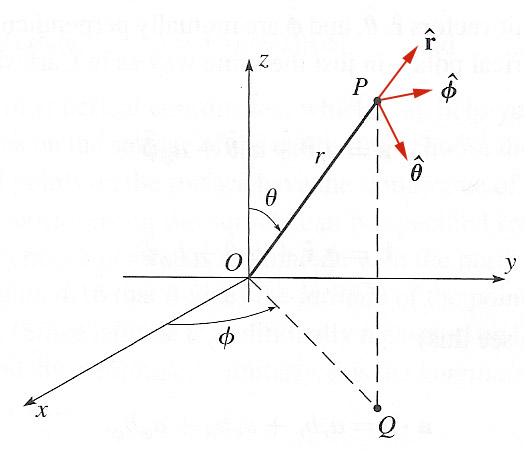
The unit vectors point in the direction that the position would change if that particular coordinate were increased.
Unlike Cartesian coordinates, these unit vector directions vary with position :-<.
But at least, the unit vectors are mutually perpendicular.
Consider two vectors with components: $$\myv a = a_r\uv{r} + a_\theta \uv \theta + a_\phi \uv \phi,$$ $$\myv b = b_r\uv{r} + b_\theta \uv \theta + b_\phi \uv \phi.$$
Only if the tails of the two vectors lie in the same radial direction from the origin do the unit vectors point the same directions for both vectors. Only then can their dot product be computed from: $$\myv a \cdot \myv b = a_r b_r + a_\theta b_\theta + a_\phi b_\phi$$
But, $\myv a\cdot\myv b=ab \cos \alpha$ still works.
(Here I'm using $\alpha$ as the angle between the vectors, so as not to confuse it with $\theta$ in spherical coordinates).
Change in position
The differential change of the position vector in Cartesian coordinates $$d\myv l=dx\,\uv x+dy\,\uv y+dz\,\uv z.$$ How to find the components of $d\myv l$ in spherical-polar coordinates?
In particular, if the individual coordinates change by this much... $$r \to r + dr,$$ $$\theta \to \theta + d\theta,$$ $$\phi \to \phi + d\phi,$$ By how much has the position changed, $d\myv l$??
By what distance has the position changed??
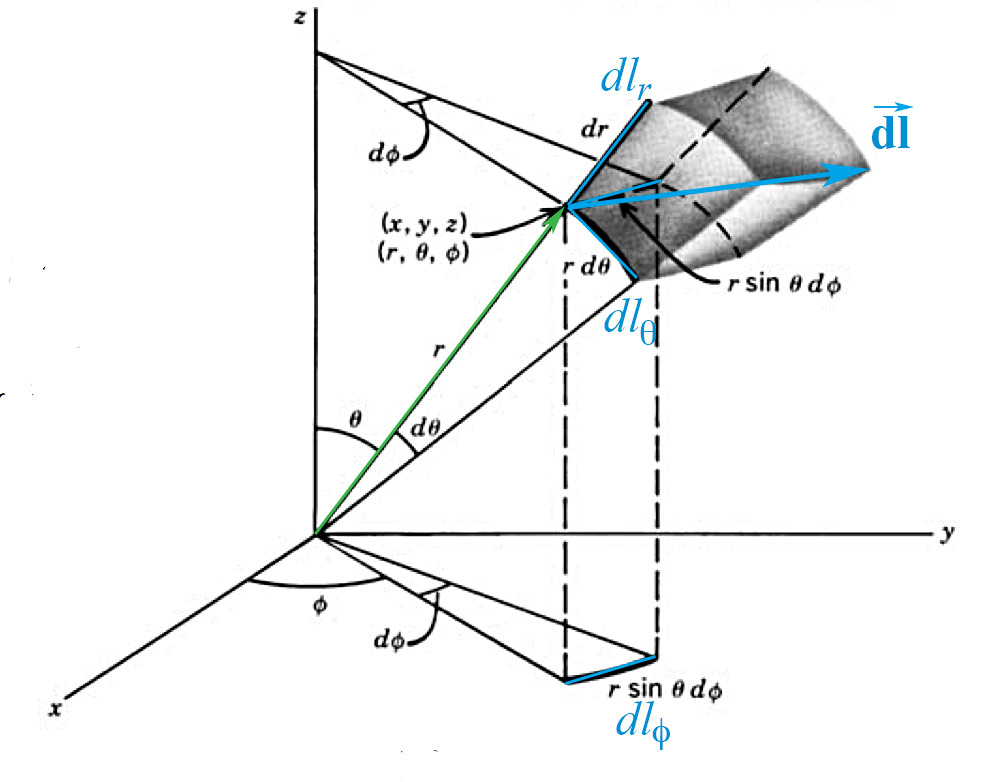
The position vector, $\color{green}{\myv r}$, is the green vector in the figure above. $d\myv{l}$ is a
small change in position.
$$d\myv l = dl_r\,\uv r +dl_\theta\,\uv\theta +dl_\phi \uv\phi.$$
If the radius coordinate changes $r \to r+dr$, then there is a change in position of $$dl_r\,\uv{r}= dr\,\uv{r}.$$
But if $\theta$ changes $\theta \to \theta+d \theta$, the change in the position of $P$ is not $d \theta \,\uv \theta$. For one thing, the units of $d \theta$ are not a distance. The distance that $P$ moves for a given $d \theta$ depends on how far away $P$ is from the origin. The distance that $P$ moves is given by the angle arc formula. The correct change in position is $$dl_\theta\, \uv \theta= r d \theta \,\uv \theta.$$
If $\phi$ changes $\phi\to \phi+d \phi$, then the change in position is again given by the angle arc formula, but this time the distance to the center of rotation is $r\sin \theta$, so $$dl_\phi \, \uv \phi= r \sin \theta\, d \phi\, \uv \phi.$$
Putting together these three changes in mutually perpendicular directions, we can write the net change in position as $$d \myv l= dr\,\uv{r} +r d \theta\, \uv \theta + r \sin \theta \,d \phi\, \uv\phi.$$
An infinitesimal volume element $d\tau$ at position $(r, \theta, \phi)$ is... $$d \tau = dl_r dl_\theta dl_\phi = r^2\sin \theta\, dr \,d \theta\, d \phi$$
Curvilinear coordinates
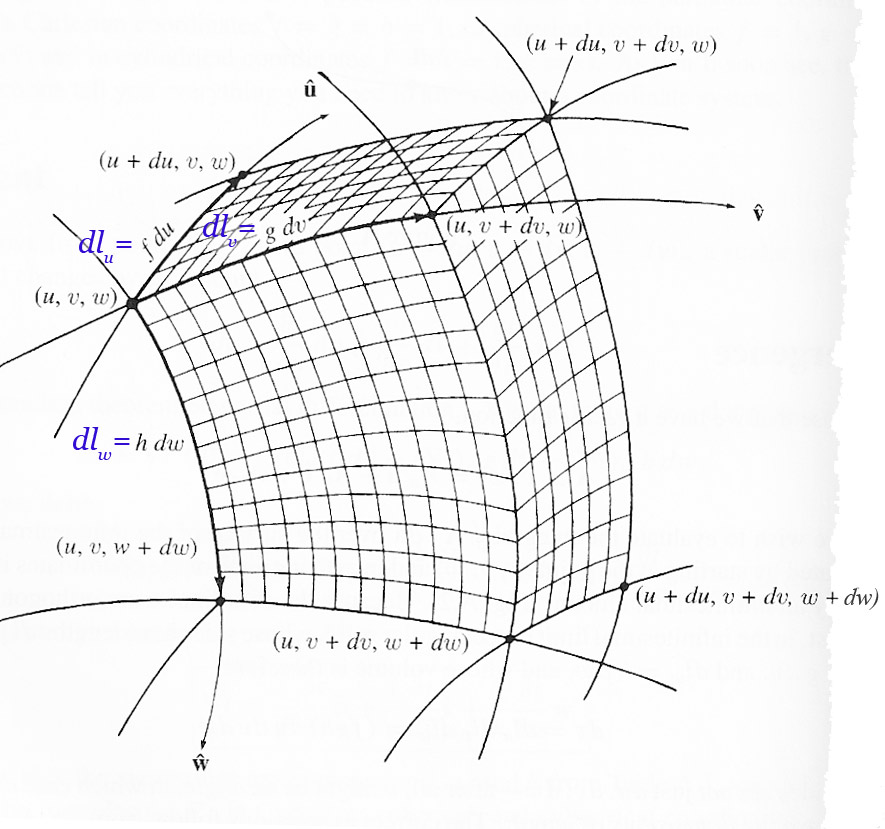
There is a whole class of curvilinear coordinate systems which share the following characteristics,
- Any position can be written uniquely with three coordinates $u$, $v$, $w$ in the system.
- The three unit vectors $\uv{u}$, $\uv{v}$, and $\uv{w}$ which point in the direction of increase of each coordinate are mutually orthogonal,
- The direction of each unit vector may change, but it is a function of the position $(u,v,w)$ in space.
These include spherical coordinates $(r,\theta,\phi)$, cylindrical coordinates $(s,\phi,z)$, and Cartesian coordinates $(x,y,z)$.
The displacement $d\myv{l}$ can be written in any of these systems in this rather abstract way: $$d\myv{l} = f\,du\,\uv{u} + g \,dv\,\uv{v} + h\, dw\,\uv{w},$$ where $f=f(u,v,w)$, $g$, and $h$ are each functions of the position.
In the ones we're familiar with...
Cartesian: d$\myv{l} = dx\,\uv{x} + dy\,\uv{y} + dz\,\uv{z}$:
$f=1$; $g=1$; $h=1$.
Cylindrical: $d \myv l = ds\,\uv{s} + r d\phi \,\uv \phi + dz\,\uv{z}$:
$f=1$; $g=r$; $h=1$.
Spherical polar: $d \myv l= dr\,\uv{r} +r d \theta\, \uv \theta + r \sin \theta d \phi
\,\uv \phi$:
$f=?$; $g=?$; $h=?$ [show / hide] the answer...]
$f=1$; $g=r$; $h=r\sin \theta$.
The gradient
It is still true for any scalar function $T$ of three variables (whether those variables represent positions in a spherical polar coordinate system, or the number of oranges in a box of fruit) that: $$dT = \frac{\del T}{\del u}du + \frac{\del T}{\del v}dv+\frac{\del T}{\del w}dw.$$
Now, we can write $dT$ as the dot product of a gradient and a general displacement $d\myv{l}$: $$dT = \myv \grad T\cdot d\myv{l} = (\myv \grad T)_u f\, du +(\myv \grad T)_v g\, dv + (\myv \grad T)_w h \,dw.$$
In order for this to be identical to the equation just before it, the gradient in this general system must have the form... $$\myv \grad T =\uv{u} \frac{1}{f}\frac{\del T}{\del u} +\uv{v} \frac{1}{g}\frac{\del T}{\del v} +\uv{w} \frac{1}{h}\frac{\del T}{\del w}.$$
Now, we just plug in the functions $f$, $g$, $h$ for the coordinate system du jour and voila! we have the gradient toute de suite! For example, in spherical polar coordinates, the gradient is...
Find in spherical coordinates: ([show / hide]) $$\myv \grad T = ?$$
Volume element
From the case of spherical polar coordinates, you might suspect--correctly!--that the
infinitesimal volume in any of these systems can be constructed as:
$$d \tau = d l_u \, d l_v \,d l_w = fdu\,gdv\,hdw=\color{blue} fgh \,du \, dv \, dw.$$
Divergence and Curl
From Appendix A, the general curvilinear expression for the divergence (A.8) is $$\myv \grad \cdot \myv A = \frac{1}{fgh}\left[\frac{\del}{\del u}(ghA_u)+\frac{\del}{\del v}(hfA_v) +\frac{\del}{\del w}(fgA_w)\right].$$
There's another such expression for the curl...which I'll refer you to in the Appendix! (A.13)