Integral vector calculus
Electrodynamics makes use of line, surface, and volume integrals.
1-d: line integrals
How to calculate the work (energy) needed to move a charge $q$ from $a$ to $b$ in an electric field $\myv E (\myv r)$?
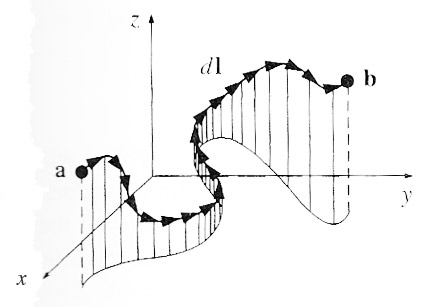
We know the force on $q$ is $\myv{F}_e=q\myv{E}$. So, the work done by the field on a charge when it moves a short, straight-line distance $d\myv{l}$ is $$dW = \myv{F}_e \cdot d\myv{l}= q\myv{E} \cdot d\myv{l}.$$
Adding up these little chunks of work along a particular path $\cal{P}$ connecting $a$ and $b$ gives us the total work: $$W = \int_{\cal P} dW = \int_{\cal P} \myv{F}_e \cdot d \myv l.$$
This is a line integral
$d \myv l$ is an infinitesimal vector 'step' or 'line segment' along the path or 'arc' ${\cal P}$.
Notation for a line integral around a closed path ... $$\oint \myv F_e \cdot d\myv{l}.$$
Parameterizing line integrals
One way to calculate a line integral is to parameterize the expressions to be integrated in terms of the arc length $l$ along the path of integration ${\cal P}$.
Write $d\myv{l}$ as $$\begineq d\myv{l} &= \uv x\,dx+\uv y\,dy+\uv z\,dz\\ &=\left(\uv x \frac{dx}{dl} + \uv y \frac{dy}{dl} + \uv z \frac{dz}{dl}\right)dl \equiv\uv l\, dl. \endeq$$ The quantity in parenthesis must be $\uv l$, which is known in Calc III as the unit tangent vector "$\uv T$": $$\uv T \equiv \uv l \equiv \frac{dx}{dl}\uv x + \frac{dy}{dl}\uv y + \frac{dz}{dl}\uv z.$$
A vector field $\myv v(x,y,z)$ has components which are functions of the single parameter $l$ along the path: $\myv v (x,y,z) = \myv v (x(l), y(l), z(l))$.
Now, we can turn a line
integral in multiple dimensions into a definite integral
of a function of one variable, $l$, and then use single-variable calculus:
$$\int_\cal{P} \myv v \cdot d\myv{l}=
\int_\cal{P} \myv v\cdot \uv l\,dl=\int_{l(a)}^{l(b)} \left(v_x \frac{dx}{dl}
+ v_y \frac{dy}{dl} + v_z\frac{dz}{dl}\right) dl.
\label{paramint}$$

Now you should go ahead and re-read these Calc III strategies for solving path integrals, where $d\myv l$ is written as $d\myv r$.
Write this one out for use in example...
Example...
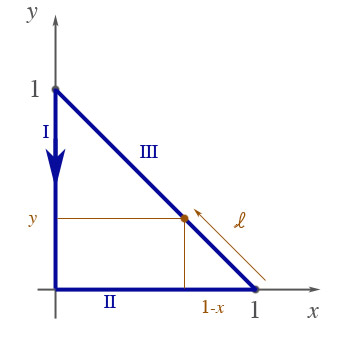 Find the line integral of $\myv v (x,y,z)= y\,\uv x - x\,\uv y$ along the
triangular path shown, in a counter-clockwise sense.
Find the line integral of $\myv v (x,y,z)= y\,\uv x - x\,\uv y$ along the
triangular path shown, in a counter-clockwise sense.
Estimate:
- Sketch, and write an expression for the unit tangent vector for each segment.
- Sketch $\myv v$ at a few locations along each segment shown.
- What is the sign of $\myv v \cdot \uv l$ for each of your sketched locations?
- Estimate for each segment whether $\int \myv v\cdot \uv l\,dl$ is positive / negative / zero.
- Estimate whether the overall magnitude of $\oint_{\cal P} \myv v \cdot d\myv l$ is going to be positive / negative / zero.
Now, do it exactly: Start by splitting this up into three pieces... $$\oint_{\cal P} \myv v\cdot d\myv l = \int_I \myv v\cdot d\myv l + \int_{II} \myv v\cdot d\myv l + \int_{III} \myv v\cdot d\myv l .$$
Segment I:
Along the $y$-axis, $\myv v=y\,\uv x$ only has an $x$ component. Since the tangent vector is $\uv l = -\uv y$, the tangential component of $\myv v$ is $y \uv x \cdot -\uv y=0$ and so $\int_I \myv v\cdot d\myv l=0$.
Segment II:
Along the $x$-axis, $v=-x\,\uv y$ and $d\myv l = dl \,\uv x$ are once more at right angles, and so $\int_{II} \myv v\cdot d\myv l=0$.
Segment III:
- Come up with expressions for $x(l)$, $y(l)$, and $z(l)$ along the path...
$$\ \ y(l)=l/\sqrt 2;\ \ x(l)=1-l/\sqrt 2; z(l)=0;$$
When we integrate, $l$ will run from 0 to $\sqrt 2$.
- Find $dx/dl,\ dy/dl,\ dz/dl$:
Differentiate $x(l)$ w.r.t $l$: $$\frac{dx}{dl}=\frac{d}{dl}(1-l/\sqrt 2)=-1/\sqrt 2.$$ Similarly, we find $\frac{dy}{dl}=1/\sqrt 2;\ \frac{dz}{dl}=0$.
- Write out $\myv v (x(l),y(l),z(l))$: $$\begineq \myv v &= y(l)\uv x -x(l)\uv y\\ &=\frac{l}{\sqrt 2}\uv x -(1-\frac{l}{\sqrt 2})\uv y \endeq$$
- Write out the integral ($\ref{paramint}$) and solve it:
$$\begineq \int_{III} \myv v\cdot d\myv l &= \int_{l(a)}^{l(b)} \left[ v_x \frac{dx}{dl} + v_y \frac{dy}{dl} + v_z\frac{dz}{dl}\right]\, dl\\ &=\int_{0}^{\sqrt 2} \left[ \frac{l}{\sqrt 2}\left(\frac{-1}{\sqrt 2}\right) -\left(1-\frac{l}{\sqrt 2}\right)\frac{1}{\sqrt 2} + 0 \right]\,dl \\ &=\int_{0}^{\sqrt 2} \left[ l\left(\frac{-1}{2}+\frac{1}{2}\right)-\frac{1}{\sqrt 2} \right]\,dl \\ &= \int_{0}^{\sqrt 2} \left[ -\frac{1}{\sqrt 2} \right]\,dl=\left. -\frac{l}{\sqrt 2}\right|_0^{\sqrt 2} = -1. \endeq$$
So, for this function, $$\oint_{\cal{ P}} \myv v \cdot d \myv l = \int_I \myv v\cdot d\myv l + \int_{II} \myv v\cdot d\myv l + \int_{III} \myv v\cdot d\myv l=0+0-1=-1.$$
The amazing thing is that there is a class of vector functions for which line integrals do not depend on the path, but only on the endpoints.
More about those in a bit.
Surface integrals
This is a surface integral of the vector field $\myv v$ over the surface $\cal S$: $$\int_\cal{S} \myv v \cdot d\myv a.$$
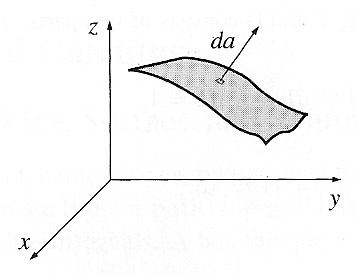 Here,
$d\myv a$ is an infinitesimal surface normal. There is a small, flat chunk of area (a real estate 'lot') on the surface. The size of this lot is $da$. The direction of $d\myv a$ is perpendicular to the surface.
Here,
$d\myv a$ is an infinitesimal surface normal. There is a small, flat chunk of area (a real estate 'lot') on the surface. The size of this lot is $da$. The direction of $d\myv a$ is perpendicular to the surface.
If $\cal{S}$ is a closed surface, then $d\myv a$ points outwards from the enclosed surface. Otherwise, for a non-closed surface as pictured here, there's a bit of ambiguity about its direction. It could be directed as shown, or exactly 180${}^0$ away from the direction shown.
If $\myv v$ represents the flow (mass / area / time) of water, then this surface integral is the total mass of water per unit time passing through the surface, or the "flux" of water.
The amazing thing is that there are certain kinds of vector fields where the flux does not depend on the particular surface of integration, but only on the line bounding the surface.
Volume integrals
What's the mass of air inside of a balloon?

Let's say the mass density of the air is given by a function $\rho(x,y,z)$ (units: mass/volume).
We need to integrate the density over all points inside the volume (represented by $\cal V$) of the balloon: $$M=\int_{\cal V} \rho \,d \tau ,$$ where $d \tau$ is an infinitesimal volume: $d\tau = dx\,dy\,dz$ in Cartesian coordinates, and has units of volume.
If the density had been uniform, the mass would have been: $$M=\rho \int_{\cal V} \,d \tau=\rho \cal V .$$
You can find the (vector) position of the center of mass of a body by doing a volume integral: $$\myv R_{CM} = \frac{1}{M}\int_{\cal V}\rho(\myv r) \myv r\, d \tau.$$
Fundamental theorems
The integral of a "derivative" of $f$ over an "interval" depends only on $f$ at the "boundary" of the interval.
The terms in quotes have different names in different situations/dimensions.
Functions of one variable
You know this is as the fundamental theorem of calculus: $$\int_a^b f'(x)\, dx = \int_a^b \frac{df}{dx} dx=\int_{f(a)}^{f(b)} df = f(b)-f(a).$$
In words:
"Adding up the (local rate of change of the function per unit $x$) $\cdot dx$
as we go from $a$ to $b$ gives the total change in the function betwen $a$
and $b$."
Fundamental theorem for gradients
$$\int_{\cal P} \myv \grad T\cdot d\myv{l} = T(\myv b) - T(\myv a),$$since a small change in the scalar function $T$ is $dT=\myv \grad T\cdot d\myv{l}$ as the result of a step $d\myv l$ along the line connecting $a$ and $b$.
Oooh! Path independence!
Another corollary of this is that around any closed path, since the beginning and ending points are the same.... $$\oint \myv \grad T\cdot d\myv{l} = 0,$$
Notice that we are not saying that just any old function integrated along a path will depend only on something at the endpoints. This is only true for functions which are gradients.
Here is an example of a function which is smooth and continuous. In cylindrical
coordinates ($s$ is the radius) the direction and magnitude of the maximum slope at any point on the augur blade is
$$\myv p (s,\phi) = \frac{\Delta h}{2 \pi s}\,\uv \phi$$

But if move once around a circle at constant $s$, integrating over $d\phi$ we'll get $\Delta h$, the height difference from one blade edge to the next--a non-zero.
Fundamental theorem for divergence
See Stokes and Divergence theorems. The Calc III we never quite got too!
The fundamental theorem for divergences says... $$\int_{\cal V} (\myv \grad \cdot \myv v) d \tau = \oint_{\cal S} \myv v \cdot d \myv a.$$
Intuition about the divergence theorem - Khan Academy, 9 min
- Plumbing analogy: Let $\myv v$ be the is the velocity flow of an incompressible fluid.
- Then the divergence $\myv \grad \cdot \myv v$ represents liquid being added (or disappearing) 'from another dimension'.
- The integral on the right is the total flow leaving the volume through the surface. (Where else would it leave to??).
- So, because the fluid is incompressible, whenever new fluid is injected into a volume, an equal amount of fluid must leave through the bounding surface.
This also goes by...
- Gauss' theorem
- Green's theorem
Fundamental theorem for curls
$$\int_{\cal S} (\myv \grad \times \myv v) \cdot d\myv a = \oint_\cal{P} \myv v\cdot d\myv l$$
This also goes by the name of...
-
Stokes' theorem
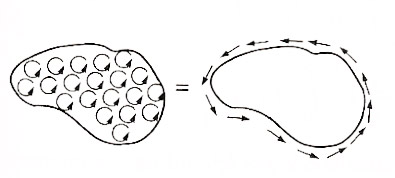
Paraphrasing.... The total "swirl" added up on a surface can be calculated by going around the edge of the surface and adding up the component of the flow parallel to the edge.
Stokes' theorem intuition - Khan Academy, 12 min
There's nothing in there about which surface. So, the integral of the curl over all surfaces which share the same boundary is the same. [box example]
What about the integral of swirl over a closed surface?
You can think of the boundary of a closed surface as a line which approaches zero length, so $\oint_\cal S (\myv \grad \times \myv v) \cdot d\myv a = 0$ for any closed surface. [Globe example]
Problem 1.30 involves calculating a surface integral over the bottom of this box...
Reprise
The integral of a "derivative" of $f$ over an "interval" depends only on $f$ at the "boundary" of the interval boundary.
If the "interval" is something with dimension $d$, then the "boundary" is something which has dimension $d-1$.
Integration by parts
Using the product rule: $$\frac{d}{dx}(fg) = f \frac{dg}{dx}+g\frac{df}{dx}$$
Integrating both sides... $$(fg)|_a^b = \int_a^b f \frac{dg}{dx} dx + \int_a^b g\frac{df}{dx} dx$$
Re-arranging just a bit... $$\int_a^b f \frac{dg}{dx} dx = (fg)|_a^b - \int_a^b g\frac{df}{dx} dx$$
Every now and then, this gives you a useful way of solving an integral that looks otherwise un-doable, if you can recognize the pattern.
For example... $$\int_0^\pi \theta \sin\theta \ d \theta=?$$
Treat $\sin\theta$ like $d (-\cos \theta)/d \theta$, and then we can re-write the integral...
$$\begineq \int_0^\pi \theta \sin(\theta)\ d \theta&= -\theta \cos\theta\left.\right|_0^{\pi} -\int_0^{\pi}-\cos\theta\ d \theta=\\ &= \pi+\sin\theta|_0^\pi = \pi\endeq$$