Vector algebra
Much of Griffith's first chapter is a review of vector calculus. Here are my notes from Multivariable Calculus / Calc III.
- Vectors and scalars.
- The dot product and cross product.
- What is a vector? ...It's how it transforms.
Vectors and Scalars
4 dollars plus 3 dollars always sums to 7 dollars.
Dollars are an example of a scalar quantity that possesses magnitude. Scalars add simply.
I'll write scalars as lower-case, italic variables, e.g. cost $c$, or height $h$.
But if you leave your house and walk 4 miles in one direction, and then 3 miles in another direction, there is no guarantee that you are 7 miles from home.
You need more information...
Displacement is an example of a vector quantity that has both magnitude and direction.
I'll write vectors as bold letters with an arrow over them, e.g. a displacement $\myv s$. Many authors use a bold, non-italic font, e.g. $\bf s$.
The magnitude of a vector is a scalar: $$|\myv s| = s$$.
Other names for magnitude
- length
- measure
- norm
A unit vector is a vector. But its magnitude is always 1. $|\uv x|=1$. I'll write a unit vector with a 'hat' over it, e.g. $\uv x$.
How do you make a unit vector pointing in the same direction as some random, not-necessarily-unit vector $\myv m$ ??
Position, Change of position
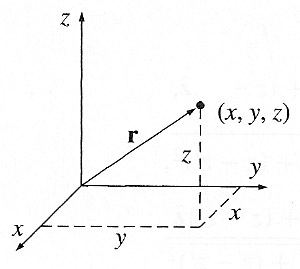
As usual, we use $\myv r$ to denote the position in space relative to the origin.
$$\myv r = x \uv x +y \uv y+z \uv z.$$Your textbook author prefers to to use $d\myv{l}$ for a small change in the position vector $\myv r$. $$d \myv{l} = dx\,\uv{x} + dy\,\uv{y}+dz\,\uv{z}.$$
Why not "$d \myv{r}$"?
Many textbooks do use $d\myv r$ to indicate an infinitesimal change in a vector $\myv r$. (Or $\Delta \myv r$ to indicate a finite change in $\myv r$).
There's no obvious advantage when working in Cartesian coordinates. But when we start using spherical or polar coordinates, it's easier not to have to worry if "$dr$" means...
- the change in the radial distance coordinate $r$?, or
- the magnitude of the change of the position vector?
We'll now be using $dl$ for #2 and $dr$ for #1.
Relative separation
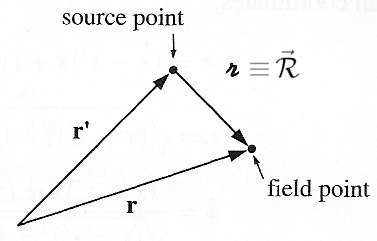
In Electrodynamics we will repeatedly have to deal with two positions:
- The position $\myv r'$ of some "source" point (usually the location of a charge), and
- A position $\myv r$ at which we want to figure out or measure the field.
Avoid confusion: $\myv r' \neq \frac{d\myv r}{dt}$! Here $\myv r'$ is just a different vector from $\myv r$.
The field usually depends on the relative separation of the two positions $\myv r - \myv r'$, which I'll call: $$ \myv r - \myv r' \equiv \myv \rr .$$
Scalar and vector functions
A function, $f(x)$, is something like a rule or relation that returns some unique value, depending on its argument(s) (dependent variable(s)).
Temperature is an example of a scalar function of three variables (coordinates).
There is a unique temperature (a scalar quantity) at any place in the room.
Temperature is a scalar function of position $(x,y,z)$, which we write as $$T(x,y,z).$$
To specify the wind, or the acceleration of gravity, we'd need to associate a vector with a position relative to the earth. A rule or relation that returns a unique vector depending on its argument(s) is a vector valued function.
Wind velocity is a vector valued function
of position:
$$\myv{W}(x,y,z).$$
Scalar times a vector = a vector.
 $a\myv V$ is a vector with the same
direction as $\myv V$ (perhaps modified by a negative sign) and with magnitude
$$ |a\myv V| = |a||\myv V|.$$
$a\myv V$ is a vector with the same
direction as $\myv V$ (perhaps modified by a negative sign) and with magnitude
$$ |a\myv V| = |a||\myv V|.$$
Dot product (scalar product)
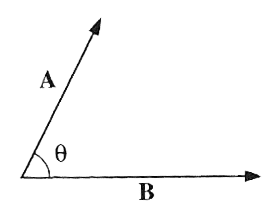
In a form which is independent of the coordinate system used, the dot product is $$\myv A \cdot \myv B \equiv |\myv A||\myv B|\cos \theta.$$ Often I'll write this as: $$\myv A \cdot \myv B \equiv AB \cos \theta.$$ with the understanding that the $A$ is a non-negative scalar that really means $|\myv A|$.
A vector dotted into itself
$$\myv C \cdot \myv C =|\myv C||\myv C|\cos 0= |\myv C|^2=C^2.$$
Pro tip Vectors & scalars can be used (like units) to do "sanity checks" on your work: An equation that works out to a scalar (vector) on the left hand side must also work out to a scalar (vector) on the right-hand side.
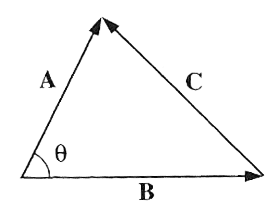 You can use $\myv C
= \myv A - \myv B$, with this definition of the dot product to remember the Law
of Cosines, by calculating $\myv C \cdot \myv C$ and expressing it in terms of $A$, $B$, and $\cos \theta$...
You can use $\myv C
= \myv A - \myv B$, with this definition of the dot product to remember the Law
of Cosines, by calculating $\myv C \cdot \myv C$ and expressing it in terms of $A$, $B$, and $\cos \theta$...
In Cartesian coordinates
$$\myv A \cdot \myv B = (A_xB_x + A_yB_y + A_zB_z).$$
Sagemath


You can combine the Cartesian and coordinate-system-independent forms of the dot product to solve problems such as...(Problem 1.3): What is the angle between the body diagonals of a cube...?
Cross product (vector product)
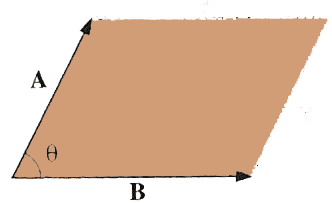 The cross product of two vectors is a vector with magnitude:
$$|\myv A \times \myv B|
= AB\sin\theta$$
which is the same as the area of the trapezoid shown.
The cross product of two vectors is a vector with magnitude:
$$|\myv A \times \myv B|
= AB\sin\theta$$
which is the same as the area of the trapezoid shown.
 But the
cross product is a vector with a direction $\uv{n}$ which is perpendicular
to both $A$ and $B$ according to a right-hand rule:
$$\frac{\myv A \times \myv B}{|\myv A \times \myv B|}\equiv \uv n.$$
But the
cross product is a vector with a direction $\uv{n}$ which is perpendicular
to both $A$ and $B$ according to a right-hand rule:
$$\frac{\myv A \times \myv B}{|\myv A \times \myv B|}\equiv \uv n.$$
- Stretch the fingers on your right hand towards $\myv A$.
- Curl your fingers towards $\myv B$ (in the direction in which $\theta < 180^o$,
- Your thumb points in the direction of $\uv{n}$.
$$\myv A \times \myv B \equiv AB\sin\theta \,\uv{n}.$$
With the right hand rule, the order in which the two vectors are "crossed" matters: $$\myv A \times \myv B = - \myv B \times \myv A.$$
The cross product is not generally distributive. Try coming up with a set of three vectors such that... $$(\myv A \times \myv B) \times \myv C \neq \myv A \times (\myv B \times \myv C).$$
RH Cartesian coordinate system
In a right-handed coordinate system: $\uv{e}_1 \times\uv{e}_2 =\uv{e}_3$. We will always take a Cartesian system where: $$\uv{x} \times\uv{y} =\uv{z}.$$
By compiling all the other unit vector products individually, e.g. $\uv{z} \times \uv{z} = 0;\ \uv{y} \times\uv{x} = -\uv{z}$; etc. you can eventually find that $$\begineq\Rightarrow \myv A \times \myv B &= (A_x\uv{x} +A_y\uv{y}+A_z\uv{z}) \times (B_x\uv{x} +B_y \uv{y}+B_z\uv{z})\\ &= (A_yB_z-A_zB_y)\uv{x} + (A_zB_x-A_xB_z)\uv{y} +(A_xB_y-A_yB_x)\uv{z}\endeq.$$
I remember this as the determinant of the three-by-three matrix shown below, which you evaluate by
adding the red products,
and subtracting
the blue products for this determinant:

SageMath

1.4
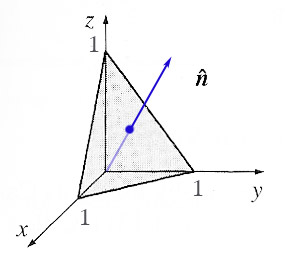 Can you see how to use the cross-product to find the direction of the normal
to the surface pictured at right? (From symmetry, what do you expect the direction
to be?)
Can you see how to use the cross-product to find the direction of the normal
to the surface pictured at right? (From symmetry, what do you expect the direction
to be?)
Transform of $\myv A \times \myv B$ in a rotated coordinate system, illustrating how to go about problem 1.10.
Vector algebra in Mathematica

What is "direction"?
Can we represent the contents of a box of apples and oranges as a vector? Let:
$$\myv N = N_a\uv{a} + N_o\uv{o}.$$
If another box has ...
$$\myv M = M_a\uv{a} + M_o\uv{o},$$
we can certainly "add" the two quantities in a vector-ish, Cartesian-y kinda way...
$$\myv{N} + \myv{M} = (N_a + M_a)\uv{a} + (N_o + M_o)\uv{o},$$
and everything looks hunky dory.
Read the section in Griffiths about this, and respond on Moodle about 'What is direction'?
But the vectors that we're used to in physics, such as the displacement vector, can be described in a variety of....
different coordinate systems:
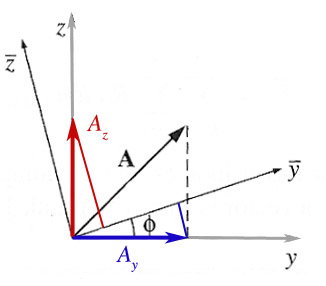
For example, if one coordinate system is rotated by an angle $\phi$ relative to another: The vector has 'components' in both the original coordinate system and the new coordinate system:
$$\myv A = A_y\uv{y} + A_z\uv{z}=A_{\bar y}\uv{\bar y} + A_{\bar z}\uv{\bar z}.$$
We can still add the two vectors $A_y\uv{y}$ and $A_z\uv{z}$ in the new coordinate system, but these two vectors are not pointing directly along one of the new component directions. If we add the projections of these two vectors along the new $\bar y$ direction we should get the $\bar y$-coordinate of the vector $\myv A$ in the new system:
$$A_{\bar y} = A_y \cos \phi + A_z\sin \phi.$$
It turns out that the $\bar z$ component is...
There's more (commented out)