Calculus of variations
We are about to delve into what appears to be a rather theoretical question about finding paths that minimize some integral expression.

Flickr member dernico71
But we shall see that this results in a new approach:
- finding and solving equations of motion,
- using scalars, instead of vectors,
- can be applied to many more problems than Newton's $\myv F=m\myv a$.
Path integral approach to mechanics
You have a bit of experience with path integrals from chapter 4.
So, let's take on a new class of problems:
- Consider some quantity that can be expressed as a path integral...
- What is the path out of all possible paths that minimizes the quantity?
Before figuring out how the minimization part of things work, here are two examples of quantities that depend on a path integral:
Shortest path
What's the shortest path $y(x)$ of all possible paths between points 1 and 2?
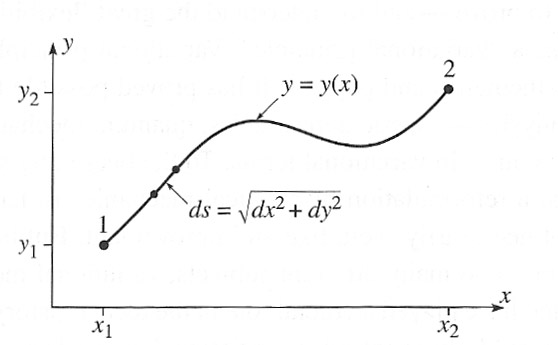
The quantity of interest is the length of the path connecting 1 and 2. If we draw in schematically the path as in the diagram, the total length is given by adding up (integrating) little arclength segments $ds$ along a specified path. $$\text{pathlength}\equiv L=\int_1^2 ds.$$
Using... $$ dy = \frac{dy}{dx} dx = y'(x) dx,$$
we can rewrite $ds$ in terms of just one small differential instead of two: $$\begineq ds =& \sqrt{dx^2 + dy^2} = \sqrt{dx^2 +(y'(x)\, dx)^2} \\ =& \sqrt{1+ y'(x)^2}\, dx.\endeq$$
The total length of the path from 1 to 2 is... $$L = \int_1^2 ds = \int_{x_1}^{x_2} \sqrt{1+y'(x)^2} dx.$$
So, here, $y(x)$ is the function that specifies the path from 1 to 2, and so the problem is to find the function that minimizes this integral.
[It is more restrictive than we'd like to have to limit ourselves to functions....why? But this is a good starting point.]
You should already know what function $y(x)$ minimizes this length $L$--right??? So we can use that as a check later on...
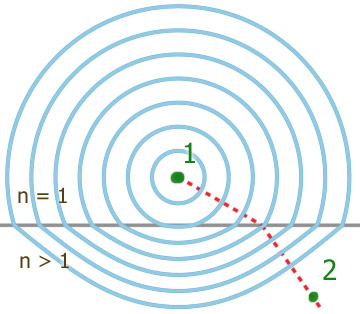
Fermat's principle
Pierre de Fermat (-1665) formulated optics based on the principle that light takes the path which minimizes the time, $\Delta t$, for light to travel between two points. The (wave) speed $v$ at which light moves in a medium of index of refraction $n$ is $v=c/n$. So Fermat's principle involves finding the path y(x) that minimizes: $$\begineq \Delta t = & \int_1^2 dt = \int_1^2 \frac{ds}{v} = \frac{1}{c}\int_1^2nds =\\ =& \frac{1}{c}\int_{x_1}^{x_2} n(x,y(x)) \sqrt{1+y'(x)^2}\,dx\endeq$$