Force as the (negative) gradient of potential energy

Multivariate vector calculus

Aw, Let's just go hiking!

 

Earth's surface can be thought of as a graph of potential energy for a particle of mass $m$ rolling around on the surface: Gravitational potential energy = $mgh$. So, the surface height $h(x,y)$ is proportional to $U$.

Partial derivatives

On a contour or topographical map, points of equal height are connected by contour lines.

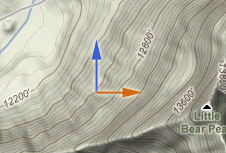$(\del U)/ (\del x)$ - slope (change in height) as you move east (no change in north/south direction). In the picture it's a positive slope as you move east.

$(\del U) / (\del y)$ - slope as you move north. In the picture, a negative slope in this direction.

See these visualizations of partial derivatives and directional derivatives.

Direction of greatest slope

How would you figure out in which direction the slope is greatest?

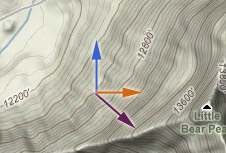It ought to be somewhere between:

• east - the direction that the height was increasing for $x$-motion, and
• south - the direction that the height was increasing for 'y'-motion (since the height was decreasing when we moved north.

We also probably ought to weight the direction more towards either $x$ or $y$ depending on which slope (partial derivative) was greater.

Putting all this together, $$\frac{\del U}{\del x} \uv{x} + \frac{\del U}{\del y} \uv{y} \equiv \myv{\grad} U.$$

This vector, the gradient turns out to have all of these characteristics:

• points in the direction of greatest increase of the height,
• its magnitude is the steepest slope out of all directions away from that point.
• it points "uphill" perpendicular to the contour line.

Skiers talk about a "fall line"-the direction of steepest descent, or the direction that water would flow away from a particular point on the mountainside. $-\myv{\grad} U$ points in the direction of the fall line. (Though, if we're picky, it doesn't actually point down the mountain slope, only points in the same $x$-, $y$-direction of the fall line, but with no $h$-component).

 

Force as the gradient of potential energy

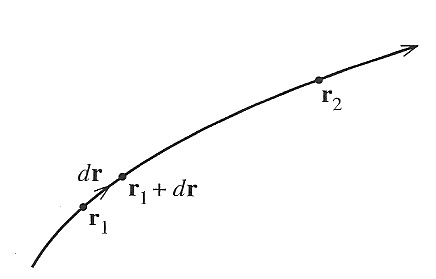
The work done by a force on a particle moving moving from $\myv{r}$ to $\myv{r} + d \myv{r}$ is: $$\begineq W(\myv{r} \rightarrow \myv{r} + d \myv{r}) =& \myv{F}(\myv{ r}) \cdot d \myv{r}\\ =&F_x dx + F_y dy + F_z dz\endeq$$

On the other hand, if the force is conservative, the work is minus the change in potential energy $$\begineq W(\myv{r} \rightarrow \myv{r} + d \myv{r}) =& -dU = -[U(\myv{r} + d \myv{r}) - U(\myv{r})]\\ =& -[U(x+dx, y+dy, z+dz) - U(x,y,z)]\\ =& -\left[\frac{\del U}{\del x} dx + \frac{\del U}{\del y} dy + \frac{\del U}{\del z} dz \right]\endeq$$

The last two equations are for the same work, and since $dx$, $dy$, and $dz$ are independent of each other, their coefficients must each be the same in the two equations, therefore: $$F_x = -\frac{\del U}{\del x},\ F_y = - \frac{\del U}{\del y},\ F_z = - \frac{\del U}{\del z}.$$

Which could also be written... $$\myv{F} = -\frac{\del U}{\del x}\uv{x} - \frac{\del U}{\del y}\uv{y} - \frac{\del U}{\del z}\uv{z}.$$

This is just the definition for the gradient of a scalar field...

$$\myv{F} = - \myv{\grad} U.$$

Operator notation

Sometimes it is useful to think of $\myv{\grad}$ as an "operator" separate from the field it's operating on. We write:

$$\myv{\grad} \equiv \uv{x} \frac{\del}{\del x} + \uv{y} \frac{\del}{\del y} + \uv{z} \frac{\del}{\del z} $$

Looking back, we had this expression for $dU$: $$dU = \frac{\del U}{\del x} dx + \frac{\del U}{\del y} dy + \frac{\del U}{\del z} dz $$

Which we could now write as $\myv{\grad} U \cdot{ d} \myv{r}$. In general, we can write this expression for a small change in a scalar function $g(x)$ in terms of its gradient:

$$dg = \myv{\grad} g \cdot{ d} \myv{r}$$

Path independence of a field

One of the conditions for a force to be conservative is that the work $\int_1^2 \myv{F} \cdot{ d\myv{r}}$ is independent of the path between 1 and 2.

It turns out that if the "curl of $\myv{F}$" vanishes, then that path integral only depends on the endpoints. (This is a consequence of Stokes' theorem.) The curl is defined as... $\myv{\grad} \times \myv{F} \equiv \det\begincv \uv{x} & \uv{y} &\uv{z}\\ \del/\del x& \del/\del y& \del/\del z \\ F_x& F_y& F_z\endcv = 0$

More on the gradient and curl in my Classical fields notes.

Does the curl of the uniform gravitational force $\myv{F}_g = -mg \,\uv{z}$ vanish? Let's try it... $$\begineq \myv{\grad} \times \myv{F}_g =& \det \begincv \uv{x}& \uv{y}& \uv{z}\\ \del/\del x& \del/\del y& \del/\del z\\ 0& 0& -mg\endcv = \\ =& \uv{x} \frac{\del}{\del y}(-mg) + \uv{y} \frac{\del}{\del x}mg =\\ =&-0 \uv{x}+0 \uv{y} = \color{blue}{0}\endeq$$

Homework

10 (a & c), 12 (c & d), (review the chain rule, or how to take the derivative of composite functions) 15, [23]