Linear approximations - Tangent planes and differentials [10.4]

The board is tangent to the bowling ball at the point of contact.
Tangent planes
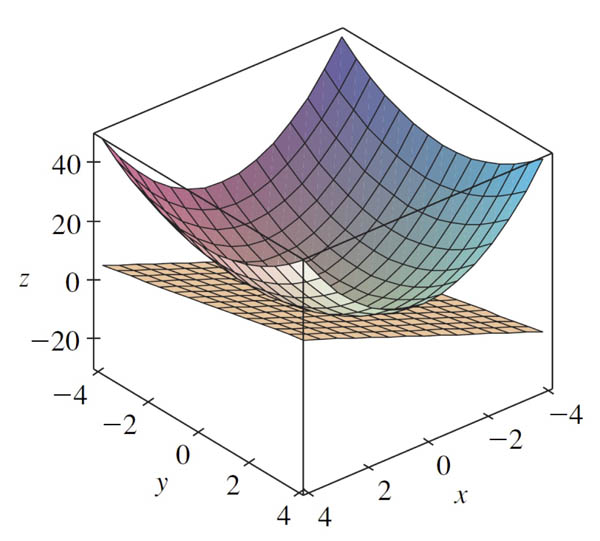
Suppose $f$ has continuous partial derivatives, and it's differentiable. An equation of the plane which is tangent to the surface $z=f(x,y)$ at the point $P(x_0,y_0, z_0)$ is $$z=z_0+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$$ Differentiating this expression, holding $y$ constant we find... $$z_x=f_x(x_0,y_0)\qquad\text{and}\qquad z_y=f_y(x_0,y_0).$$ So, at the point of contact $x_0,y_0,z_0$ the slope of the function in the $x$ direction and the slope of the function in the $y$ direction exactly match the corresponding slopes of the tangent plane.
Linear approximation
...geometric view
Any smoothly varying, continuous curve looks like a straight line if we zoom in far enough.
A smoothly varying varying shape--say a sphere--looks like a flat plane if we zoom in far enough. (Or if the inhabitants of the sphere are already very tiny in comparison!)

Chris [Flickr user sparkyc]
So, the tangent plane should be a pretty good approximation to the original function, as long as $x$ and $y$ are "not too far" from the point of contact (which in this diagram, I'm saying has coordinates $(a,b)$): $$f(x,y) \approx f(a, b) + f_x(a, b)(x – a) + f_y(a, b)(y – b)$$ is called the linear approximation or the tangent plane approximation of $f$ at $(a, b)$.
I could re-arrange this a bit to write things in terms of the change of the function: $\Delta z\equiv f(x,y)-f(a,b)$ to find out, and picture, how that depends on changes in $x$ and $y$, and how it compares with $dz$, which is the change in the height of the tangent plane: $$\Delta z \approx f_x(a,b)\Delta x+f_y\Delta y.$$
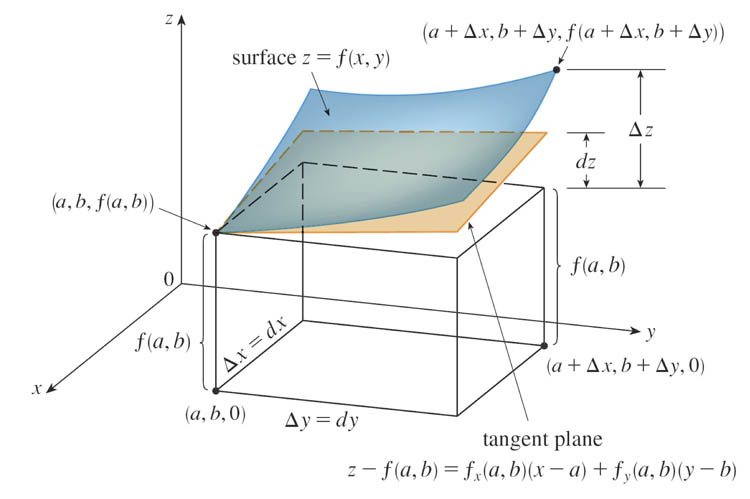
In the limit of vanishingly small 'steps', $\Delta x\to dx$ and $\Delta y\to dy$, the linear approximation becomes exact:
The differential of $f$ is $$dz\equiv df = f_x(x,y)\,dx+f_y(x,y)\,dy = \frac{\del f}{\del x}dx+ \frac{\del f}{\del y}dy.$$
This only works if there's a unique plane tangent to the surface--See the textbook for a fuller discussion--and if the function is differentiable:
Differentiability
If $z=f(x,y)$, then $f$ is differentiable at $(a,b)$ if $\Delta z$ can be expressed in the form $$\Delta z = f_x(a,b) \Delta x + f_y(a,b) \Delta y + \epsilon_1 \Delta x +\epsilon_2 \Delta y$$ where $\epsilon_1\to 0$ and $\epsilon_2 \to 0$ as $(\Delta x, \Delta y)\to 0$.
Theorem: If the partial derivatives $f_x$ and $f_y$ exist near $(a,b)$, and if they are continuous at $(a,b)$, then $f$ is differentiable at $(a,b)$.
In hiking terms:
Use the linear approximation to calculate your change in height as you step in different directions.
Unless your next step is off the edge of a cliff.
...or you're on a sharp ridge (with no unique tangent plane).
To Do
- Finish Tabular data
- Finish Graphical data