Nonright triangles
Basic concepts
- For a right triangle with side lengths $a$ and $b$ and hypotenuse $h$, these are related by: $$a^2+b^2=h^2.$$
-
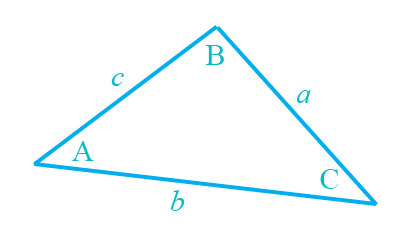The interior angles of any triangle sum to 180${}^o$:
$$A+B+C=180^o.$$
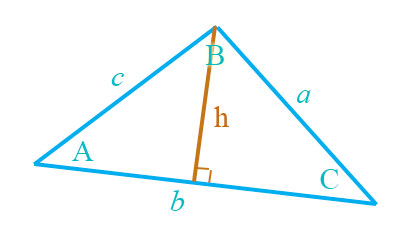The area of any triangle is $\frac 12 (\text{base})\cdot(\text{height})$.
- Given a number $\theta$ in degrees, start from the positive horizontal axis and rotate counterclockwise $\theta$ degrees around the unit circle, coming to rest at the point $(x,y)$. Then $\cos\theta=x$ and $\sin\theta=y$, and also $\tan\theta=y/x$.
Two less obvious relationships are the law of cosines and the law of sines...
Law of Sines
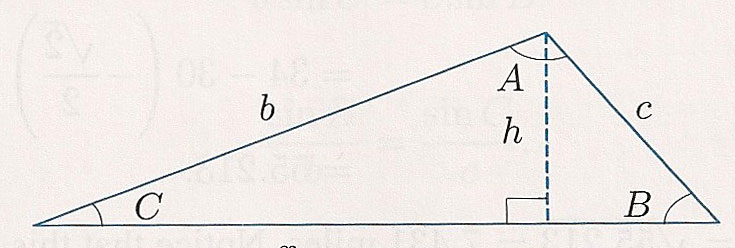
Write out $\sin B$ and $\sin C$ in terms of quantities on the diagram...
.
.
.
This is the Law of Sines:
Given any triangle with angle measures $A$, $B$, and $C$, and the opposite sides of length $a$,$b$, and $c$, then (law of sines):
$$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}.$$
Law of cosines
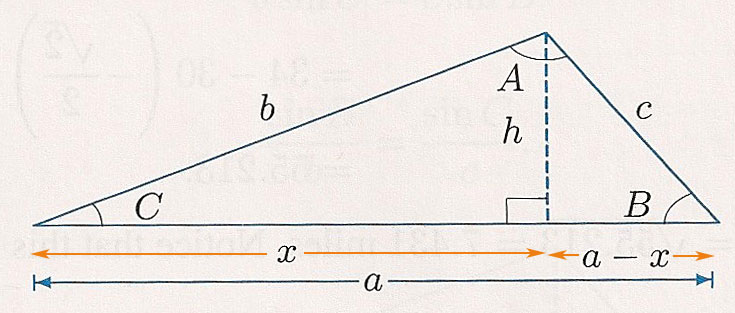
We're going to apply Pythagoras' to the right triangle, the left triangle, and eliminate $x$ to get a relationship between $a$, $b$, $c$ and $\cos C$.
.
.
.
This is the Law of Cosines:
$$c^2=a^2+b^2-2ab\cos C.$$
It holds for any triangle, even if $C$ is not an acute angle.
Problems
[7.6] Nonright triangles - ProblemsSolutions [Mathematica file]