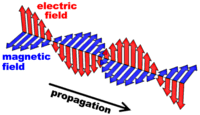
 An
E-M wave is apparently a disturbance in the electromagnetic field
around a charge, because of its motion.
An
E-M wave is apparently a disturbance in the electromagnetic field
around a charge, because of its motion. Shake some electric charges... you get an E-M wave.
Every wave is a disturbance.
 An
E-M wave is apparently a disturbance in the electromagnetic field
around a charge, because of its motion.
An
E-M wave is apparently a disturbance in the electromagnetic field
around a charge, because of its motion.
This is not anything material--Weird!
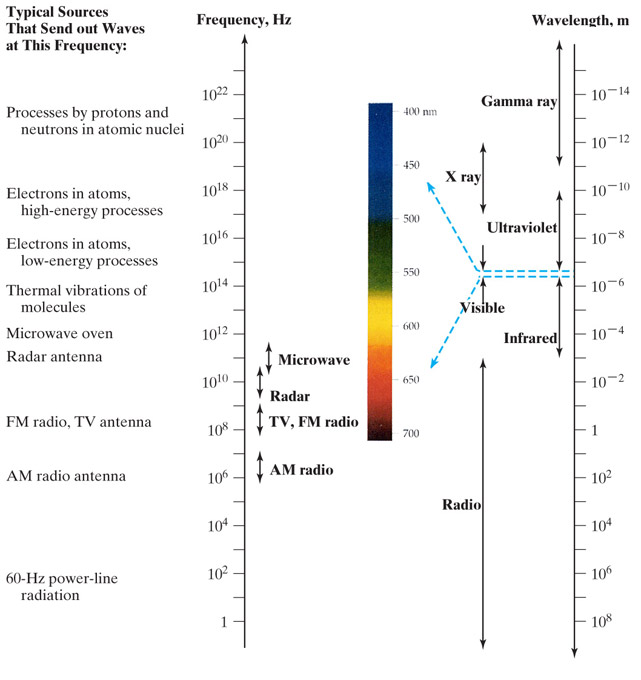
Experimentally, it is found that things like AM radio waves and microwaves all travel at the same speed: 300,000 km / sec...
...the same as the speed of light.
Sound only travels where there's air.
Does light require air...or anything material to travel in?

When you heat objects up, they start to visibly glow. First a dull red, through yellow, to "white"-hot.
Microscopically: Higher temperatures = faster speeds of particles = more frequent bouncing into others = higher frequencies of being knocked back and forth....
Why shouldn't these randomly shaking particles give rise to E-M field waves, just like the shaking electrons in a radio antenna?
Light is also an electromagnetic wave.
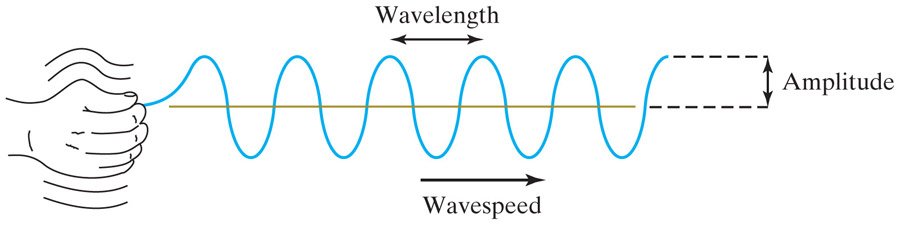
Wavelength = distance between crests in [m] (or [m / (wave)])
Wavespeed - units [m/s]
Amplitude = maximum distance away from 'undisturbed' (yellow line) - units [m]
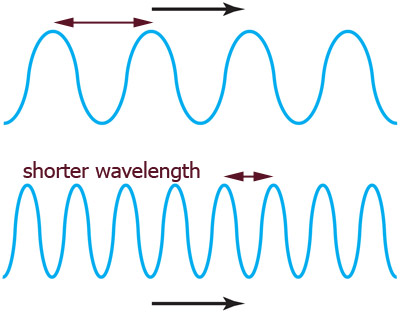 Frequency =
# of waves passing a point in a time interval - [1/s] or [(cycles)/sec] or
[Herz] =[Hz]
Frequency =
# of waves passing a point in a time interval - [1/s] or [(cycles)/sec] or
[Herz] =[Hz]
Seems like a larger frequency $implies$ smaller wavelength
${\rm w a v e l e n g t h} \propto \frac{1}{\rm f r e q u e n c y}$
All other things being equal, Higher frequency wave carries more energy than lower frequency wave*: Imagine boats on the ocean being tossed up and down by these two waves.
The picture below shows pipes carrying the exhaust gases out of a racecar engine. The pipes are so hot that they're glowing. How would you describe the regions that are colder? Are they less bright? or are they more red?

Our sun has a surface temperature of ~5400 C~5700 K.
A Tungsten lightbulb filament has a melting temperature of ~3700 K.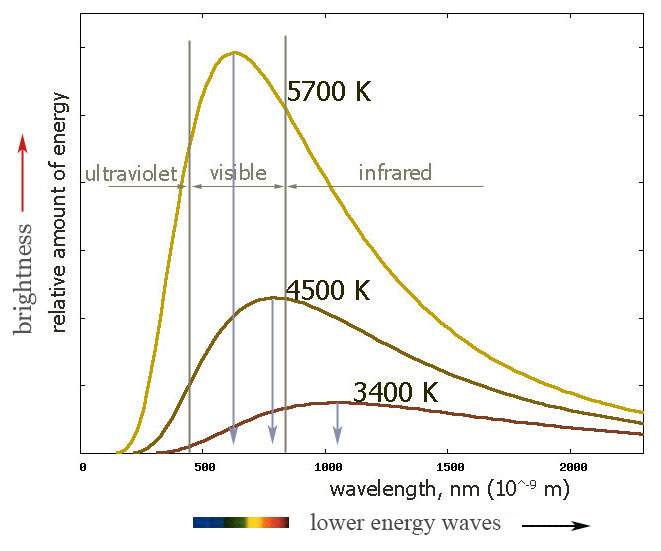
The temperature of a glowing object is closely related to its apparent color.
Do we "glow" too, just like the sun, just with a peak around 300 K?
Yes. this corresponds to the infrared part of the spectrum. Special sensors can sense IR, and then transpose it up into the visible range for us to see.
You can also use this technology to look for heat leaks: Here are two sets of windows on a 6th St house on the same cold night:
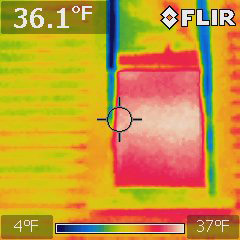 Older window |
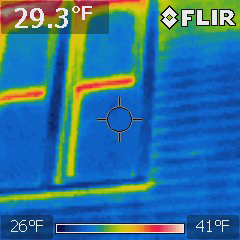 Replacement, highly insulated window |
|---|
Also notice the difference of glass' transparency when viewed in the IR and in the optical range.
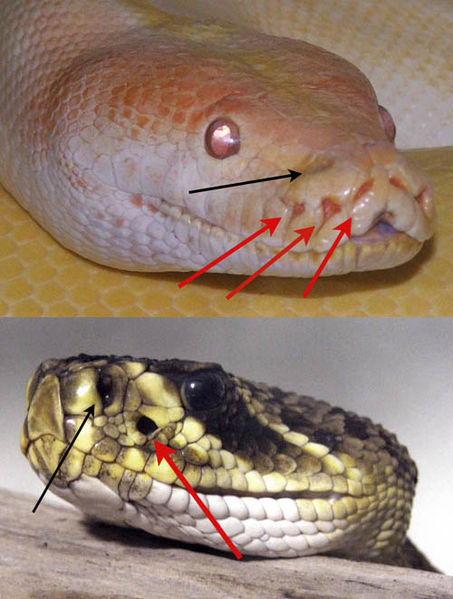
Some snakes have "pit organs" that can sense IR radiation.
"Blackbody" radiation is the radiation you'd expect from from a collection of idealized "molecules" at a particular temperature that have no internal structure.
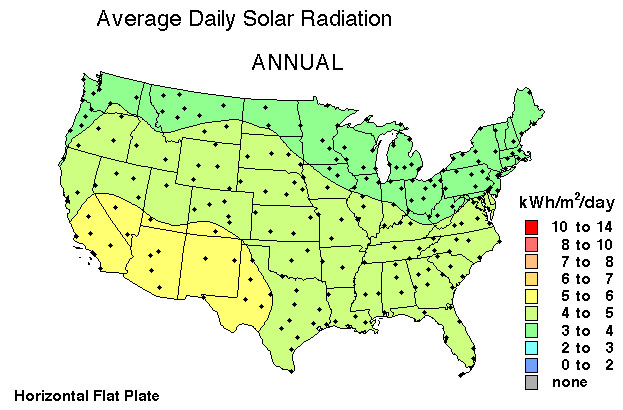
Typical family usage (Paul's!) ~$\frac{500 k W h}{m o n t h} \cdot \frac{1 m o n t h}{ 30 d a y s }$ ~17 kWh / day.
So, for 5 people, that's about 3-4 kW*hrs per day per person, the solar energy falling on 1 square meter of N. Indiana in an average day.
Current solar photovoltaic (PV) devices convert about 15% (~ 1/7) of the energy that falls on them into electricity. $\Rightarrow$ we'd need about 7 square meters of solar panels per person.
We might compare this with the land area we as a society have dedicated to another public good: the interstate highway system. It's ~75,000 km long with an average density of 1000 km${}^2$ for every 800 km of length. That's an area of 94,000 square km. Dividing this by the current population of ~300 million, this works out to ~300 square meters of Interstate per person.
There are ~300 million people in the United States. If each person needs about 7 $m^2$ what's the total area that would have to be covered with solar panels to meet all of our home electricity needs?
Approximately what is the area of Indiana in square meters? One approach might be to start with any driving times you've experienced crossing some portion of the state. You might use the ratio of ~ 1.6 km in each 1 mile.
How does the area needed to generate elecricity via PV for everyone in the United States compare to the area of Indiana--That is, what's the ratio?
Conceptual exercises: Chapter 9: 1, 4, 7, 8, 12, 15, 16
Problems: Chapter 9: 1, 3, 6